蓝桥杯 试题 历届试题 格子刷油漆

问题描述

　　X国的一段古城墙的顶端可以看成 2*N个格子组成的矩形（如下图所示），现需要把这些格子刷上保护漆。


　　你可以从任意一个格子刷起，刷完一格，可以移动到和它相邻的格子（对角相邻也算数），但不能移动到较远的格子（因为油漆未干不能踩！）
　　比如：a d b c e f 就是合格的刷漆顺序。
　　c e f d a b 是另一种合适的方案。
　　当已知 N 时，求总的方案数。当N较大时，结果会迅速增大，请把结果对 1000000007 (十亿零七) 取模。

输入格式

　　输入数据为一个正整数（不大于1000）

输出格式

　　输出数据为一个正整数。

样例输入

2

3

22

样例输出

24

96

359635897

---

解题思路:这一题的解题思路是把所有可能刷格子的情况分类，用dp解决。解题的关键和这一题最有趣的地方是宽度总是两格且不能重复刷，这带来了一个有趣的性质:

设宽度为N( N>2 )且初始位置为第K列(1<K<N)，那么如果刷完第K列的两格后就只能刷左边或右边的了(无法穿过第K列了)。

起始的格子有两种情况:从角(两端)开始刷或者从中间列开始刷。

---

先考虑从四个角的一个开始刷(N>2)：

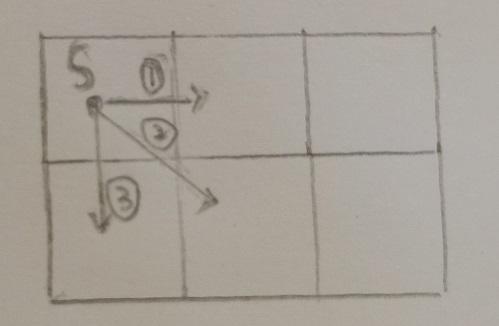
从起点S出发后第二步有三种选择，其中如果选择③即刷对格那么问题的规模由N减小为N-1.

如果第二步选择的是①或②，那么第三步有两种选择:是否刷起点S列的剩余一个。

　　•如果刷起点S列的剩余一个那么第四步就是把前两列(针对画图的这一情况)刷完了,之后问题的规模从N减小为N-2,且有①②两种情况。

　　•如果不刷起点S列的剩余一个那么只能最后一步再刷(如果在第k列(k>2)回头那么第k列的两个就都刷完了，那么就不能再刷k列右边的了(根据此题特殊的性质))

所以之后的的移动只能选择下一列的两格的一个，直到刷到第N列回头。

用数组Traverse[ N ]表示N列从一个角出发的所有可能，TraverseBack[ N ]表示从角S出发最后一步回到S列剩余格子的情况，有递推式:

 •TraverseBack[ N ] =  2 * TraverseBack[ N-1 ]  = 2^(N-1)  //可以理解为从N减小为2个N-1规模(如果只看N-1规模那么其最后一步也是回到起点列的剩余一格)/或者每一步都有两种情况

 •Traverse[ N ] = TraverseBack[ N ] + 2 * Traverse[ N-1 ] + 4 * Traverse[ N-2 ] 

/*其中2*Traverse[ N-1 ] 就是第二步是③的情况，而4*Traverse[ N-2 ] 是第三步回到S列的剩余一格，有①②两种情况,而剩余规模N-2的起点又有两种可能，所以总共4种*/

---

接下来考虑起点从中间列开始的情况(N>3，这时才有中间列，即1<K<N-1)

又根据此题特殊的性质，刷的顺序只能是先刷完一边(侧)再回到起点列剩余一格，再刷另外一边。以第K列为例:

先刷左边再刷右边的方案数: 第K列有两格 ，且是最后一步回到起点列，所以是2*TraverseBack[K]，接着右边起点也有两种可能，且此时没有回到右边起点列的限制，所以是2*Traverse[ N-K ] 

综合即 4 * TraverseBack[ K ] * Traverse [ N- K ]

注意如果先刷右边，此时的问题规模是N- K +1 ,而左边的规模是 K-1。

---

//解题完整代码

#include<cstdio>

typedef long long ll;

const int Max_N = 1000;
const ll Mod = 1000000007;//取余 

//输入
int N;

ll Traverse[Max_N+1]; //不返回 
ll TraverseBack[Max_N+1];  //返回

void solve()
{
    //初始化 (因为递推公式条件是N>2,所以N<=2要单独处理 )
    TraverseBack[1] = 1;
    Traverse[1] = 1;
    TraverseBack[2] = 2;
    Traverse[2] = 6;
    //特殊处理 (没有四个角) 
    if( N==1 ){
        printf("%d
",2*Traverse[N]);
        return;
    }
    
    for(int i=3; i<=N; i++)
    {//递推式 
        TraverseBack[i] = (2*TraverseBack[i-1])%Mod;
        Traverse[i] = (TraverseBack[i] + 2*Traverse[i-1] + 4*Traverse[i-2])%Mod;
    }    
    
    ll res = (4*Traverse[N])%Mod;//四个从角出发 
    for( int i=2; i<N; i++)
    {//遍历从边出发 
        res = (res + 4 * TraverseBack[i] * Traverse[N-i])%Mod;//先刷左边 
        res = (res + 4 * Traverse[i-1] * TraverseBack[N-i+1])%Mod;//先刷右边 
    }
    
    printf("%lld
",res);
} 

int main()
{
    scanf("%d",&N);
    
    solve();
    
    return 0;
}

//参考代码https://blog.csdn.net/so_so_y/article/details/79763823实际上博主递推式与其叙述不符，但因为问题有对称性所以答案正确，也可以当做一个思路。

//参考java代码https://blog.csdn.net/s1293678392/article/details/78966189