0.PTA得分截图

1.本周学习总结
1.1 总结栈和队列内容
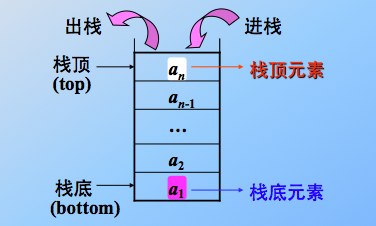
栈的存储结构及操作
栈其实本质还是线性表:限定仅在表尾进行插入或删除操作。 俗称:后进先出 ,也可说是先进后出(FILO),栈也分为顺序和链式两大类。
栈是限定只能在表尾删除和插入操作的线性表。
由于栈本身就是一个线性表,所以线性表的操作特性它都具备,针对它的特殊性,在它的操作上可能会有一些变化。将进栈和出栈分别改名为push和pop。
用顺序存储结构存储的栈称为顺序栈。线性表是用数组来实现的。对于栈,用下标为0的一端作为栈底比较好,因为首元素都存在栈底,变化比较小。
我们定义一个top变量来指示栈定元素在数组中的位置。若存储栈的长度为MaxSize,则栈顶位置top必需小于MaxSize。当栈存在一个元素时,top等于0,因此空栈的判断条件为top等于-1.
栈的结构定义:
typedef int SElemType;
typedef struct {
SElemType data[MAXSIZE];
int top; //用于栈顶指针
} SqStack;
入栈操作:
bool Push(Stack S, ElementType X)
{
if (S->Top == S->MaxSize)
{
printf("Stack Full
");
return false;
}
else
{
S->Data[S->Top] = X;
S->Top++;
return true;
}
}
出栈操作:
ElementType Pop(Stack S)
{
if (S->Top == 0)
{
printf("Stack Empty
");
return ERROR;
}
else
{
S->Top--;
return S->Data[S->Top];
}
}
1.2关于共享栈
共享栈,即是两个栈使用同一段存储空间。
第一个栈从数组头开始存储,第二个栈从数组尾开始,两个栈向中间拓展。
当top1+1==top2或者top1==top2-1时,即有栈空
与普通栈一样,共享栈出栈入栈的时间复杂度仍为O(1).
数据结构
typedef struct shareStack{
int data[MAXSIZE];
int top1;
int top2;
}shareStack;
出栈操作
int Pop(shareStack *ss,int flag){
if(flag == 1){
if(ss->top1 == -1)
return -1;
return ss->data[ss->top1--];
}else if(flag == 2){
if(ss->top2 == MAXSIZE)
return -1;
return ss->data[ss->top2++];
}
return -1;
}
入栈操作
int Push(shareStack *ss,int num,int flag){
if(ss->top1+1 == ss->top2)
return 0;
if(flag == 1){
ss->data[++ss->top1] = num;
return 1;
}else if( flag == 2){
ss->data[--ss->top2] = num;
return 1;
}
return 0;
}
1.3栈的应用
表达式求值
中缀表达式:运算符号位于两个运算数之间。如 ,a+b*c-d/e
后缀表达式:运算符号位于两个运算数之后。如, abc*+de/-
借助一个栈来存放运算数。
优先级比栈顶运算符高写入栈
优先级比较低或者相等,出栈,写入后缀表达式中
伪代码
while (从exp读取字符ch,ch!='�')
{ ch为数字:将后续的所有数字均依次存放到postexp中,
并以字符'#'标志数值串结束;
ch为左括号'(':将此括号进栈到Optr中;
ch为右括号')':将Optr中出栈时遇到的第一个左括号'('以前的运算符
依次出栈并存放到postexp中,然后将左括号'('出栈;
ch为'+'或'-':
出栈运算符并存放到postexp中,直到栈空或者栈顶为'(',
然后将'+'或'-'进栈;
ch为'*'或'/':
若 栈顶为'*'或'/',出栈,直到栈顶不是'*'或'/'
否则 入栈
}
若exp扫描完毕,则将Optr中所有运算符依次出栈并存放到postexp中。
迷宫问题
求解思想:回溯法
从入口出发,按某一方向向未走过的前方探索
若能走通,则到达新点,否则试探下一方向 ;
若所有的方向均没有通路,则沿原路返回前一点,换下一个方向再继续试探
直到所有可能的通路都探索到,或找到一条通路,或无路可走又返回到入口点。
每个方块的数据定义:
typedef struct
{ int i; //当前方块的行号
int j; //当前方块的列号
int di;
} Box; //定义方块类型
栈定义:
typedef struct
{ Box data[MaxSize];
int top; //栈顶指针
} StType; //顺序栈类型
迷宫问题这一块比较不清楚.
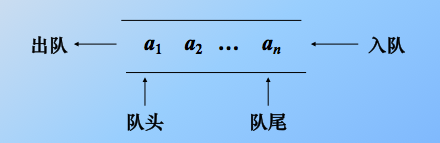
1.4队列的存储结构及操作
限定在表的一端插入、另一端删除。 插入的那头就是队尾,删除的那头就是队头。也就是说只能在线性表的表头删除元素,在表尾插入元素。
先进先出 (FIFO结构)。显然我们不能在表(队列)的中间操作元素,只能是在尾部进,在头部出去
当队列没有元素的时候,我们就说队列是空队列。
链式队列
用链表表示的队列,限制仅在表头删除和表尾插入的单链表。一个链队列由一个头指针和一个尾指针唯一确定。

顺序队列
(1)初始为空队列,那么头尾指针相等
(2)入队,那么尾指针加1,头指针不变。
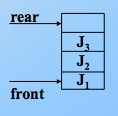
(3)出队,则尾指针不变,头指针加1,先进先出原则

(4)删除,则头指针再次和尾指针相等,说明队列空了
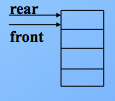
(5)在顺序队列中,当尾指针已经指向了队列的最后一个位置的下一位置时,若再有元素入队,就会发生“溢出”

循环队列
循环队列我们必须给定最大值MAXQSIZE。
当添加一个元素时,(rear+1)%MAXQSIZE
当删除一个元素时,(front+1)%MAXQSIZE
队列满:(Q.rear+1)%MAXSIZE=Q.front
队列空:Q.rear==Q.front
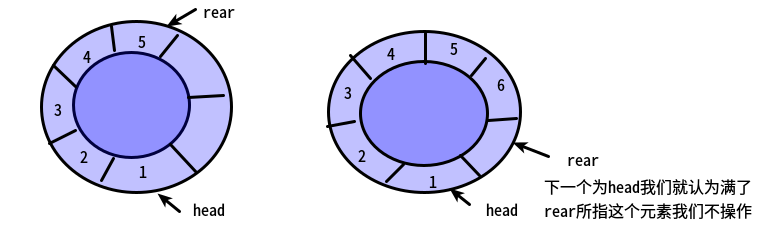
添加操作
status EnQueue(SqQueue *q,QElemtype e)
{
//插入到队尾
if((q->rear+1)%MAXQSIZE==q->front)
return 0;
q->base[q->rear]=e;
q->rear=(q->rear+1)%MAXQSIZE;
return 1;
}
删除操作
status DeQueue(SqQueue *q)
{
if(q->front==q->rear)
return 0;
printf("%d",q->base[q->front]);
q->front =(q->front+1)%MAXQSIZE;
return 1;
}
获取队列长度
int QueueLength(SqQueue *q)
{
return (q->rear-q->front+MAXQSIZE)%MAXQSIZE;
}
定义
typedef struct{
QElemtype *base;
int front;
int rear;
}SqQueue;
初始化队列
SqQueue* InitQueue()
{
SqQueue *q;
q=new SqQueue;
q->base=new int[MAXQSIZE];
q->rear=q->front=0;
return q;
}
1.5队列应用
舞伴问题
舞伴问题,利用队列将舞伴人分别存到两个性别不同的队列当中,党配对舞伴时,将其再出队列
int QueueLen(SqQueue Q)//队列长度获取
{
int length = 0;
int i = Q->front;
int j = Q->rear;
for (i = 0; i != j; i++)
{
length++;
}
return length;
}
int EnQueue(SqQueue& Q, Person e)//加入队列
{
if (Q->rear == MAXQSIZE - 1)
{
return 0;
}
else
{
Q->rear++;
Q->data[Q->rear] = e;
return 1;
}
}
int QueueEmpty(SqQueue& Q)//队列是否为空
{
return(Q->front == Q->rear);
}
int DeQueue(SqQueue& Q, Person& e)//出队列
{
if (Q->front == Q->rear)
{
return 0;
}
else
{
Q->front++;
e = Q->data[Q->front];
return 1;
}
}
void DancePartner(Person dancer[], int num)//配对舞伴
{
Person son;
int i;
for (i = 0; i < num; i++)
{
son = dancer[i];
if (son.sex == 'F')
{
EnQueue(Fdancers, son);
}
if (son.sex == 'M')
{
EnQueue(Mdancers, son);
}
}
while (!QueueEmpty(Fdancers) && !QueueEmpty(Mdancers))
{
DeQueue(Fdancers, son);
cout << son.name << " ";
DeQueue(Mdancers, son);
cout << son.name << endl;
}
}
1.2.谈谈你对栈和队列的认识及学习体会。
本周我们主要学习了栈和队列的基本操作和应用。首先来说栈,栈只能在栈顶进行操作,是先进后出,可用于符号配对,走迷宫和计算后缀表达式等。栈可以分为顺序栈和链栈,运用于不同的情况。队列是先进先出,可在队头删除,也可以在队尾插入。队列也可分为顺序队和链队,在顺序队中,为了防止假溢出,又增加了循环队列。
在C++中的stack、queue类模板中,已经有写好的函数帮我们执行一些基础函数,所以我们要学会应用C++函数。本章节还应该熟记各种栈空、栈满、队空、队满的条件,并注意在出队,出栈和取队、栈时,都应该注意判断队列、栈是否为空。
2.PTA实验作业
2.1.题目1:符号配对
2.1.1代码截图


2.1.2本题PTA提交列表说明。

Q1:编译错误
A1:因为在PTA编译器里面没有吧C改为C++编译
Q2:部分正确,栈空没有通过
A2:加上判断栈是否为空的条件
2.2.题目2:银行业务队列简单模拟
2.2.1代码截图


2.2.2本题PTA提交列表说明。
Q1:编译错误
A1:oddQu.front()误写成oddQu.front
Q2:最小的N(即N=1)时格式错误
A2:当N=1即队列中只有一个队列中有一个数时,输出的数字前会多一个空格。在源代码下面添加了
对N=1的特殊判断。
3.阅读代码
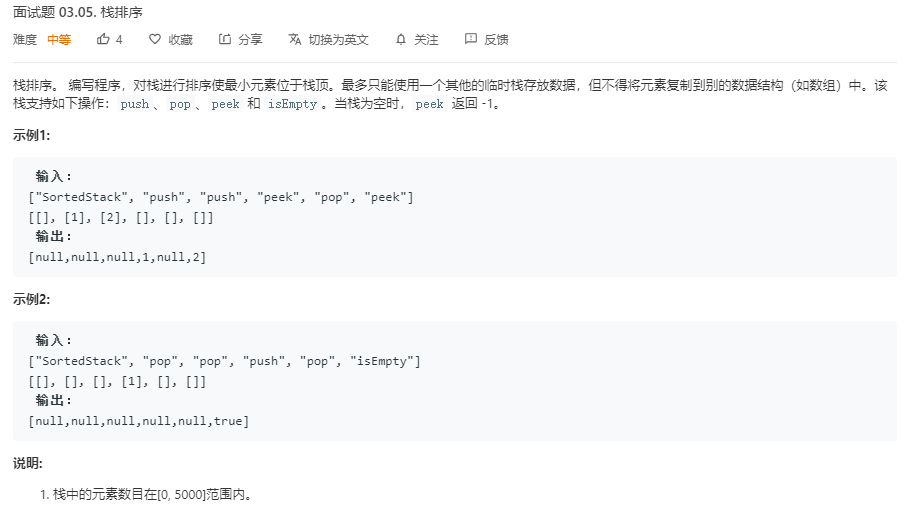
3.1 题目及解题代码
题目:
解题代码:
public class SortedStack {
Stack<int> stack = new Stack<int>();
Stack<int> temp = new Stack<int>();
public SortedStack()
{
}
public void Push(int val)
{
while (true)
{
var max = stack.Count == 0 ? int.MaxValue : stack.Peek();
var min = temp.Count == 0 ? int.MinValue : temp.Peek();
if (val > max)
{
temp.Push(stack.Pop());
}
else if (val < min)
{
stack.Push(temp.Pop());
}
else
{
break;
}
}
stack.Push(val);
}
public void Pop()
{
while (temp.Count > 0)
{
stack.Push(temp.Pop());
}
if (stack.Count == 0)
{
return;
}
stack.Pop();
}
public int Peek()
{
while (temp.Count > 0)
{
stack.Push(temp.Pop());
}
if (stack.Count == 0)
{
return -1;
}
return stack.Peek();
}
public bool IsEmpty()
{
return stack.Count == 0 && temp.Count == 0;
}
}
3.1.2该题的设计思路
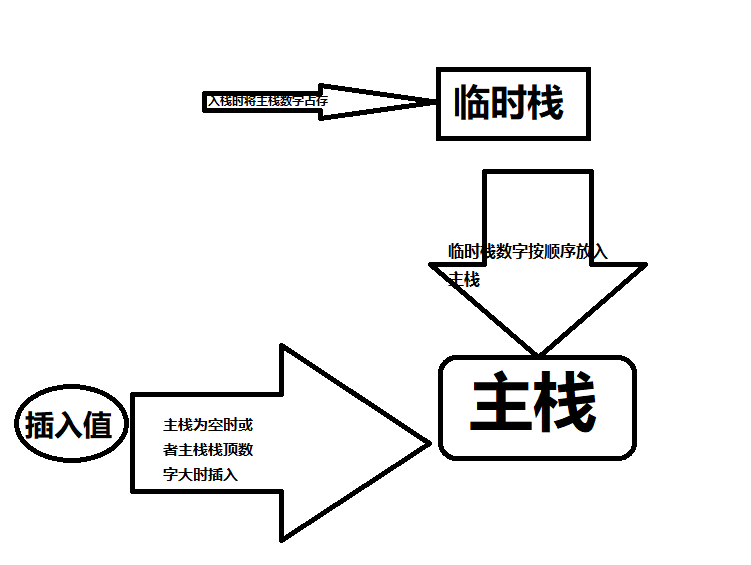
- 临时栈存放的数据永远小于主栈的数据,每次新数字入栈时,仅仅动态调整两个栈,使临时栈的数据小于插入值,主栈的数据大于插入值,然后插入数值到主栈,每次Peek或Pop时才懒惰更新将临时栈的数据全部放回主栈。
3.1.2 该题的伪代码
public class SortedStack {
Stack<int> stack = new Stack<int>();
Stack<int> temp = new Stack<int>();
public void Push(int val)
{
while (true)
{
if (主栈数据大于插入值)
{
插入数值到主栈;
}
else if (主栈数据小于插入值)
{
插入数值到主栈;
}
else
{
此时调整好了
就break;
}
}
往栈中写入数据;
}
public void Pop()
{
while (临时栈大于0)
{
将临时栈内的数据返回已有栈;
}
if (临时栈等于0)
{
返回;
}
stack.Pop();
}
public int Peek()
{
while (临时栈大于0)
{
将临时栈内的数据返回已有栈
}
if (临时栈等于0)
{
return -1;
}
}
public bool IsEmpty()
{
return stack.Count == 0 && temp.Count == 0;
}
}
3.1.3运行结果

3.1.4分析该题目解题优势及难点。
- 优势:该题通过利用双栈来完成,使得做法的空间更大更容易操作,用临时栈来存放思路更加清晰
- 难点:该题是LeetCode上找到的一道面试题,总的难度不是很大,主要是感觉判断部分比较难
3.2题目及解题代码
题目:

解题代码:
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
stack<int> st;
int n = popped.size();
int j = 0;
for (int i = 0; i < pushed.size(); ++i){
st.push(pushed[i]);
while(!st.empty() && j < n && st.top() == popped[j]){
st.pop();
++j;
}
}
return st.empty();
}
};
3.2.1该题的设计思路

思路很简单,我们尝试按照 popped 中的顺序模拟一下出栈操作,如果符合则返回 true,否则返回 false。这里用到的贪心法则是如果栈顶元素等于 popped 序列中下一个要 pop 的值,则应立刻将该值 pop 出来。
3.2.2 该题的伪代码
初始化栈 stack,j = 0;
遍历 pushed 中的元素 x;
当 j < popped.size() 且栈顶元素等于 popped[j]:
使栈顶元素出栈;
j += 1;
如果栈为空,返回 true,否则返回 false。
3.2.3 运行结果


3.2.4分析该题目解题优势及难点。
- 优势:通过pushed和st,使用st来模拟操作,将数组中的每个数依次入栈,使得思路比较清晰
- 难点:该题难度不大,就是在检查栈的程序比较复杂