0.PTA得分截图

1.本周学习总结
1.1 总结树及串内容
-
BF算法:
BF算法亦称简单匹配算法,它从主串的第一个字符开始和模式串比较,若不同则从第二个字符再次开始比较,以此类推直到匹配成功或遍历完主串。int BF(SqString s, SqString t) { int i = 0, j = 0; while (i < s.length && j < t.length) { if (s.data[i] == t.data[j]) { i++; j++; } else { i = i - j + 1; j = 0; } } if (j >= t.length) { return (i - t.length); } else { return (-1); } } -
KPM算法:
KMP算法较BF算法有较大改进之处:1.主串不需要回溯i指针 2.将模式串向右“滑动”尽可能远的一段距离int KMP(SqString s, SqString t) { int nextval[MAX]; int i, j; i = j = 0; GetNextval(t, nextval); while (i < s.len && j < t.len) { if (j == -1 || s.data[i] == t.data[j]) { i++; j++; } else { j = nextval[j]; } } if (j >= t.len) return (i - t.len); else return (-1); } void GetNextval(SqString t, int nextval[]) { int j = 0, k = -1; nextval[0] = -1; while (j < t.len) { if (k == -1 || t.data[j] == t.data[k]) { j++; k++; if (t.data[j] != t.data[k]) { nextval[j] = k; } else { nextval[j] = nextval[k]; } } else { k = nextval[k]; } } } -
二叉树存储结构:二叉树的存储结构分为顺序存储和链式存储
- 二叉树的顺序存储结构:对于完全二叉树而言,顺序存储结构是很合适的,这种存储结构也可以通过下标直接找到孩子或父亲,但如果用顺序结构存储非完全二叉树,就会造成内存的浪费,尤其是二叉树较空的时候
typedef struct { int data[MAXSIZE];//存放二叉树的节点值 int n;//节点个数 }BTree; - 二叉树的链式存储结构:二叉树的链式存储结构相比起顺序存储结构要更加的节省空间
typedef struct BiTNode { char data; //存放二叉树的节点值 struct BiTNode* lchild; //指向左孩子 struct BiTNode* rchild; //指向右孩子 }BTNode, * BTree;
- 二叉树的顺序存储结构:对于完全二叉树而言,顺序存储结构是很合适的,这种存储结构也可以通过下标直接找到孩子或父亲,但如果用顺序结构存储非完全二叉树,就会造成内存的浪费,尤其是二叉树较空的时候
-
二叉树的建法:二叉树的建立是递归建树
void CreateTree(BTree& T, string str, int &i) { if (i >= str.length()) return; if (str[i] != '#') { T = new BTNode; T->data = str[i]; i++; CreateTree(T->lchild, str, i); CreateTree(T->rchild, str, i); } else { T = NULL; i++; } } -
二叉树的遍历:二叉树的遍历可分为先序遍历、中序遍历、后续遍历及层次遍历
/*二叉树的先序遍历*/ void PreOrder(BTree T) { if (T != NULL) { cout << T->data << " "; InOrder(T->lchild); InOrder(T->rchild); } }/*二叉树的中序遍历*/ void InOrder(BTree T) { if (T != NULL) { InOrder(T->lchild); cout << T->data << " "; InOrder(T->rchild); } }/*二叉树的后序遍历*/ void PostOrder(BTree T) { if (T != NULL) { InOrder(T->lchild); InOrder(T->rchild); cout << T->data << " "; } }/*二叉树的层次遍历*/ void LevelPrintTree(BTree T) { BTree curNode; //指向当前遍历到的节点 BTree lastNode; //指向所遍历层次的最后一个节点 queue<BTree> qu; int flag = 0; int level = 0; //表示当前所在层数 curNode = lastNode = T; if (T == NULL) { cout << "NULL"; return; } qu.push(T); while (!qu.empty()) { if (curNode == lastNode) //遍历到每层的最后一个节点输出对应层数 { if (flag == 0) { cout << ++level << ":"; flag = 1; } else { cout << endl; cout << ++level << ":"; } lastNode = qu.back(); } curNode = qu.front(); cout << curNode->data << ","; qu.pop(); if (curNode->lchild) { qu.push(curNode->lchild); } if (curNode->rchild) { qu.push(curNode->rchild); } } } -
二叉树的应用:
- 表达式树:将中缀表达式转换为一棵表达式树,可用于表达式的求解
void InitExpTree(BTree& T, string str) //建表达式的二叉树 { int i = 0; stack<char> op; stack<BTree> tree; op.push('#'); while (str[i]) { if (In(str[i])) //str[i]为运算符 { if (Precede(op.top(),str[i]) == '<') //优先级大于栈顶运算符 { op.push(str[i++]); } else if (Precede(op.top(), str[i]) == '>') //优先级小于栈顶运算符 { T = new BTNode; T->data = op.top(); op.pop(); T->rchild = tree.top(); tree.pop(); T->lchild = tree.top(); tree.pop(); tree.push(T); } else //优先级相等 { op.pop(); i++; } } else //str[i]为操作数,操作数均为叶节点 { T = new BTNode; T->data = str[i++]; T->lchild = NULL; T->rchild = NULL; tree.push(T); } } while (op.top() != '#') //运算符栈不为空 { T = new BTNode; T->data = op.top(); op.pop(); T->rchild = tree.top(); tree.pop(); T->lchild = tree.top(); tree.pop(); tree.push(T); } } double EvaluateExTree(BTree T)//计算表达式树 { double sum; double lnum; //左子树的值 double rnum; //右子树的值 if (!In(T->data)) //T->data为操作数 { return T->data - '0'; } lnum = EvaluateExTree(T->lchild); rnum = EvaluateExTree(T->rchild); if (T->data == '+') { sum = lnum + rnum; } else if (T->data == '-') { sum = lnum - rnum; } else if(T->data == '*') { sum = lnum * rnum; } else if (T->data == '/') { if (rnum == 0) //除数为0 { cout << "divide 0 error!"; exit(0); } else { sum = lnum / rnum; } } return sum; }
- 表达式树:将中缀表达式转换为一棵表达式树,可用于表达式的求解
-
树的结构:
- 双亲存储结构:这种结构根据节点的parent指针很容易找到节点的双亲,但如果要找孩子节点则需要遍历整个结构
typedef struct { int data; int parent; //指向双亲的位置 }ParentTree[MaxSize]; - 孩子链存储结构:该种存储结构在查找双亲是很麻烦
typedef struct node { int data; struct node* sons[MaxSons]; //指向孩子结点 }SonTree; - 孩子兄弟链存储结构:
typedef struct tnode { int data; struct tnode* son; //指向孩子 struct tnode* brother; //指向兄弟 }SBTree;
- 双亲存储结构:这种结构根据节点的parent指针很容易找到节点的双亲,但如果要找孩子节点则需要遍历整个结构
-
线索二叉树:在二叉树的链式存储中,会有大量的空指针域,为了不浪费空间,将这些指针利用起来,我们用这些空着的指针指向线索,形成线索二叉树。
线索二叉树的结构体定义:typedef struct TNode { char data; //结点数据 struct BTNode* lchild, * rchild; //左右孩子指针 int ltag; //用于标记左右孩子是否为空 int rtal; }BTNode, * BTree;后序线索二叉树示意图:
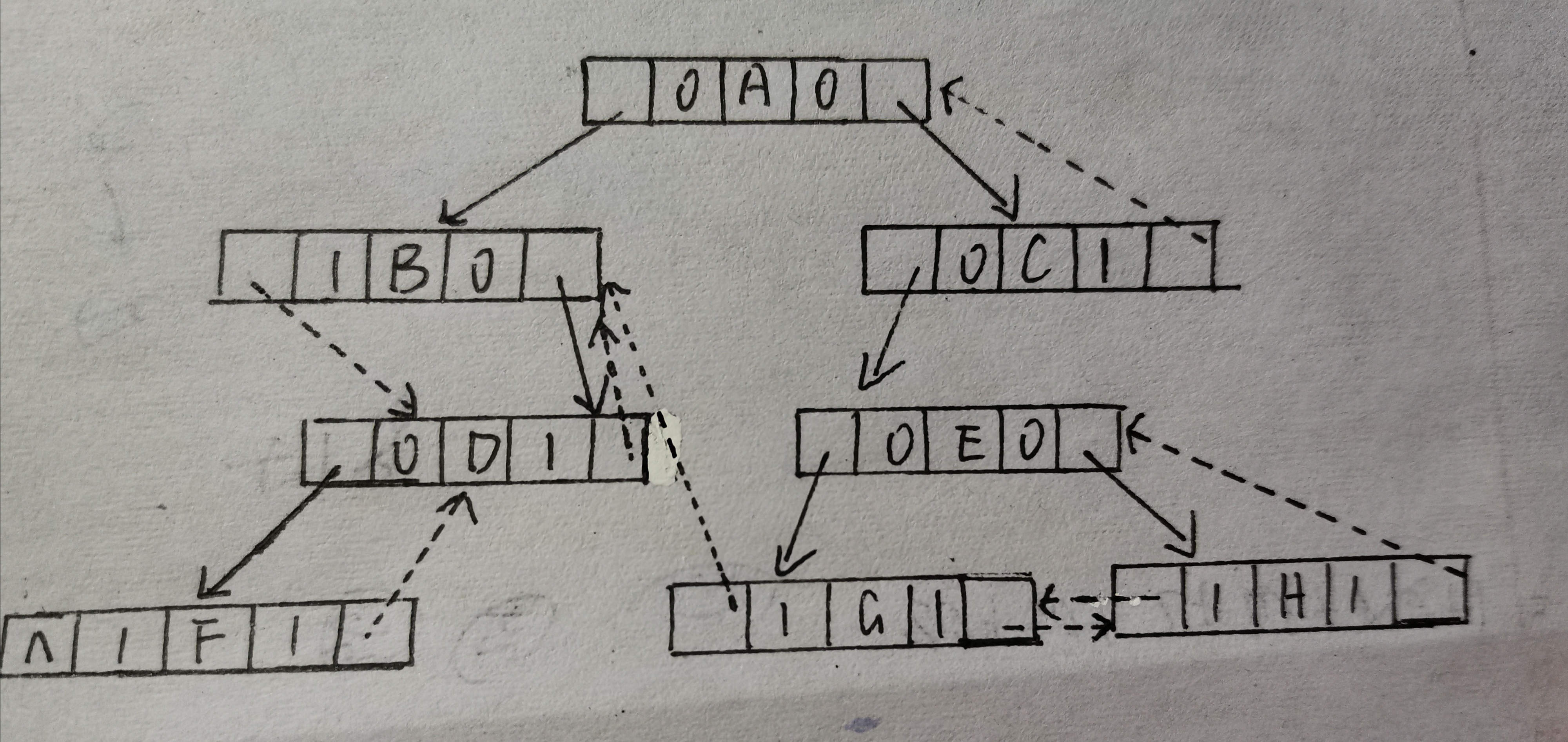
-
哈夫曼树:给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近
- 如何构造哈夫曼树:
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为: (1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点); (2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和; (3)从森林中删除选取的两棵树,并将新树加入森林; (4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
- 如何构造哈夫曼树:
-
并查集:并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。常常在使用中以森林来表示。
- 并查集有三种基本操作:初始化、合并两个集合、查找自己所在集合
- 初始化:
void MAKE_SET(UFSTree t[], int n) { int i; for (i = 0; i < n; i++) { t[i].data = i; t[i].rank = 0; t[i].parent = i; } } - 合并两个集合:
void UNION(UFSTree t[], int x, int y) { x = FIND_SET(t, x); y = FIND_SET(t, y); if (t[x].rank > t[y].rank) { t[y].parent = x; } else { t[x].parent = y; if (t[x].rank == t[y].rank) { t[y].rank++; } } } - 查找自己所在合集:
int FIND_SET(UFSTree t[], int x) { if (x != t[x].parent) //双亲不是自己 { return (FIND_SET(t, t[x].parent)); } else { return x; } }
1.2 谈谈你对树的认识及学习体会
开始学习树后,最难理解的应该就是一开始学习建树的时候了,因为建树的函数有用到递归,刚开始对于递归很不习惯,建树也很不熟练,等到写的代码多了一点后,虽然还是不熟练,但是可以理解了。
3.阅读代码
3.1 打家劫舍
题目:
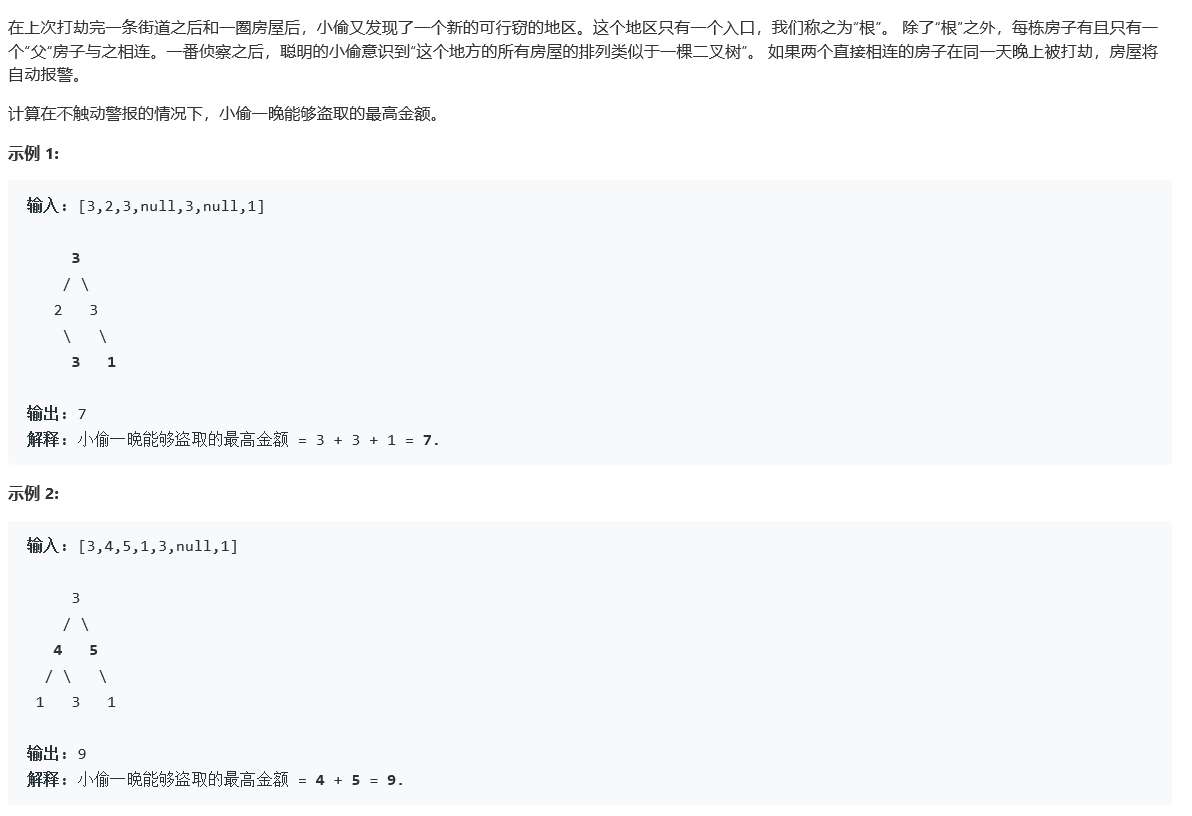
解题代码:
class Solution {
public:
int rob(vector<int>& nums)
{
if (nums.size() == 0)
return 0;
if (nums.size() == 1)
return nums[0];
vector<int> dp(nums.size(), 0);
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for (int i = 2; i < nums.size(); ++i)
{
dp[i] = max(dp[i - 1], nums[i] + dp[i - 2]);
}
return dp[nums.size() - 1];
}
};
3.1.1 该题的设计思路
建立一个nums数组存储每个房间的值,再建立一个dp数组存储每前i个房间的最优解
3.1.2 该题的伪代码
建立一个dp数组 /*第i个状态即为前i个房间能够获得的最大财宝(最优解)*/
dp[0]=nums[0];
dp[1]=max(nums[0],nums[1]);
for i=2 to i<nums.size() do
dp[i] = max( dp[i-1], nums[i]+dp[i-2] );
/*
选择第i个房间,则dp[i]为:第i个房间+前i-2个房间的最优解
不选择第i个房间,则dp[i]为:前i-1个房间的最优解
*/
end for
return dp[nums.size() - 1];
3.1.3 运行结果

3.1.4 分析该题目解题优势及难点
解题优势:建立了一个dp数组,当i>3时,最优解为dp[i-1]或者nums[i]+dp[i-2],利用该数组解决了复杂问题。
难点:因为两个点之间不能有直接联系,要在这种情况下找到可相加的最大值比较难
3.2 计算二叉树的最大宽度
解题代码:
typedef struct TreeNode* BinTree;
struct TreeNode
{
int Key;
BinTree Left;
BinTree Right;
};
int Width(BinTree T)
{
BinTree p;
Queue Q;
int Last, temp_width, max_width;
temp_width = max_width = 0;
Q = CreateQueue(MaxElements);
Last = Queue_rear(Q);//标注队尾位置
if (T == NULL) return 0;
else
{
Enqueue(T, Q);//将二叉树的树根入队列
while (!IsEmpty(Q))
{
p = Front_Dequeue(Q); //由队头出队列一个元素
temp_width++;
if (p->Left) Enqueue(p->Left, Q);//将出队列的这个元素的左孩子节点入队
if (p->right) Enqueue(p->right, Q);//将出队列的这个元素的右孩子节点入队
if (Queue_front(Q) > Last) //判断上一层是否遍历完
{
Last = Queue_rear(Q);//更新标注变量的值
if (temp_width > max_width) max_width = temp_width;
temp_width = 0;
}
}
return max_width;
}
}
3.2.1 该题的设计思路
先创建一个队列,用一个标注变量去标注最开始时队尾的位置,然后用一个循环来操作二叉树,循环体内的操作和层序遍历类似,不同的是,在每趟循环结束后都要来判断上一层是否便利完成(用那个标注变量和队首的位置比较)如果便利完成,则刷新最大宽度。
3.2.2 该题的伪代码
将二叉树的树根入队列
while(队列不为空)
{
由队头出队列一个元素赋值给p
if (p->Left) 左孩子入队
if (p->Reft) 右孩子入队
if 上一层遍历完 then
更新标注变量的值
if (temp_width > max_width) max_width = temp_width;
temp_width = 0;
end if
}
3.2.3 运行结果

3.2.4 分析该题目解题优势及难点
优点:借助“数量标注”,设置一个变量来标定你这一层的节点的数量,利用队列入队和出队时队列的队头与队尾位置关系的变化关系来达成分隔二叉树层次的作用。
难点:每一层在哪个地方结束是需要特别注意的
3.3 找树左下角的值
题目:

解题代码:
class Solution {
public:
int findBottomLeftValue(TreeNode* root)
{
if (!root->left && !root->right)return root->val;
queue<TreeNode*>q;
q.push(root);
while (!q.empty())
{
int flag = 0;//flag用来判断是否是最后一行
queue<TreeNode*> qt;
while (!q.empty())
{
TreeNode* t = q.front();
q.pop();
if (t->left)
{
qt.push(t->left);
if (t->left->left || t->left->right) flag = 1;
}
if (t->right)
{
qt.push(t->right);
if (t->right->left || t->right->right) flag = 1;
}
}
if (flag)
q = qt;
else
return qt.front()->val;
}
}
};
3.3.1 该题的设计思路
利用层次遍历,当遍历到最后一层时,找第一个节点
3.3.2 该题的伪代码
建立一个队列q
根节点入队
while(队列q不为空)
{
flag=0;
定义一个队列qt;
while(队列不为空)
{
取队头并出队赋值给t
if(t->left)
左孩子入队qt
if(左孩子为叶节点) flag=1;
end if
if(t->right)
右孩子入队qt
if(右孩子为叶节点) flag=1;
end if
}
if flag为1 then
q = qt;
else
return qt.front()->val;
end if
}
3.3.3 运行结果

3.3.4 分析该题目解题优势及难点
解题优势:利用层次遍历二叉树,当二叉树遍历到最后一层时,遍历的第一个节点为树左下角的值
难点:当你遍历到树的左下角时,你还需要判断这个点是否在最后一行,如果不是你还需要继续去找
3.4 冗余连接
题目:

解题代码:
class Solution {
public:
int findroot(int x, vector<int>& p) //查找根结点
{
if (x == p[x]) return x;
return p[x] = findroot(p[x], p);
}
void merge(int x, int y, vector<int>& arr, vector<int>& p) //路径压缩
{
int dx = findroot(x, p);
int dy = findroot(y, p);
if (dx == dy) //如果两个的根节点相同,说明加上这条边构成一个环,顾要删掉这条边
{
arr[0] = x;
arr[1] = y;
return;
}
p[dy] = dx;
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
vector<int> p(edges.size() + 1);
vector<int> arr(2); //存储要删除的两结点之间的边
for (int i = 1; i <= edges.size(); i++) //初始化
p[i] = i;
for (auto r : edges)
{
merge(r[0], r[1], arr, p); //连接两个结点
}
return arr;
}
};
3.4.1 该题的设计思路
把相连的结点连到一个根节点上,当最后加入的结点的根节点相同时,则说明此边将构成一个环,所以就去掉这条边,也就是要删掉的边。
3.4.3 运行结果

3.4.4 分析该题目解题优势及难点
解题优势:利用并查集可以比较轻松地解决该问题
难点:如何判断哪条边是多出来的,并且要保证去除这条边后结果图是一个有着N个节点的树