福哥答案2020-09-13:
首先确定b的范围,b的范围一定在[2,logN]里。然后遍历b,求a的范围,如果范围长度等于0,说明这个正整数是a的b次方。
1.遍历b范围。二分法求a,a初始范围是[2,logN]。2的400次方耗时5秒。【有代码】
2.遍历b范围。优化二分法求a,a初始范围是[2,上一次a的结果]。2的10000次方耗时5秒。【有代码】
3.应该有更优化的方案,暂时没想到。【无代码】
因为用到了大整数,所以用python语言编写。代码如下:
#!/usr/bin/python3
import time
from functools import wraps
def _get_sqrt_range(num, right, exp=2):
"""
求num的exp开方,exp是指数,num是结果。求底数。
Args:
num: 大于等于0并且是整数。
right: 大于等于0并且是整数。右边界。
exp: 大于等于0并且是整数。
Returns:
返回元组,表示一个开方范围。
Raises:
IOError: 无错误。
"""
left = 1
if num == 0:
return 0, 0
if num == 1:
return 1, 1
if num == 2 or num == 3:
return 1, 2
while True:
mid = (left + right) // 2
if mid ** exp > num:
right = mid
if left ** exp == num:
return left, left
if left + 1 == right:
return left, right
elif mid ** exp < num:
left = mid
if right ** exp == num:
return right, right
if left + 1 == right:
return left, right
if mid == 1:
return 1, 2
else:
return mid, mid
def get_log_range(num, basenum):
"""
求对数范围。
Args:
num: 数,大于等于1并且是整数。
basenum: 底数,大于等于2并且是整数。
Returns:
返回结果。对数范围。
Raises:
IOError: 无错误。
"""
if num == 1:
return 0, 0
else:
n = 0
ism = 0
while num >= basenum:
if ism == 0 and num % basenum != 0:
ism = 1
n += 1
num //= basenum
return n, n + ism
def timefn(fn):
"""计算性能的修饰器"""
@wraps(fn)
def measure_time(*args, **kwargs):
t1 = time.time()
result = fn(*args, **kwargs)
t2 = time.time()
print(f"@timefn: {fn.__name__} took {t2 - t1: .5f} s")
return result
return measure_time
@timefn
def is_power1(num):
"""
判断n是否是一个数的幂次方形式。
Args:
num: 大于等于0并且是整数。
Returns:
返回结果。true是幂数
Raises:
IOError: 无错误。
"""
if num <= 3:
return False
else:
log_range = get_log_range(num, 2)
if log_range[0] == log_range[1]:
return True
expmax = log_range[0]
expmin = 2
exp = expmin
sqrt = 0
right = 2 ** (1 + log_range[0] // 2)
while exp <= expmax:
sqrt = _get_sqrt_range(num, right, exp)
# right = sqrt[0]#缩小右边界范围
if sqrt[0] == sqrt[1]:
return True
if sqrt == (1, 2):
return False
exp += 1
return False
@timefn
def is_power2(num):
"""
判断n是否是一个数的幂次方形式。
Args:
num: 大于等于0并且是整数。
Returns:
返回结果。true是幂数
Raises:
IOError: 无错误。
"""
if num <= 3:
return False
else:
log_range = get_log_range(num, 2)
if log_range[0] == log_range[1]:
return True
expmax = log_range[0]
expmin = 2
exp = expmin
sqrt = 0
right = 2 ** (1 + log_range[0] // 2)
while exp <= expmax:
sqrt = _get_sqrt_range(num, right, exp)
right = sqrt[0] # 缩小右边界范围
if sqrt[0] == sqrt[1]:
return True
if sqrt == (1, 2):
return False
exp += 1
return False
if __name__ == "__main__":
print("----2的400次方")
num = 2 ** 400 + 1
print(is_power1(num))
print(is_power2(num))
print("
----2的10000次方")
num = 2 ** 10000 + 1
print(is_power2(num))
执行代码结果如下: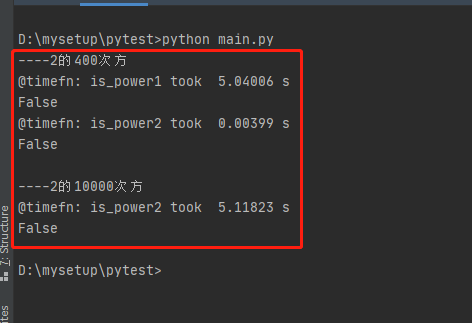
***
[评论](https://user.qzone.qq.com/3182319461/blog/1599951713)