2020-10-05：如何求模平方根？

福哥答案2020-10-05：#福大大架构师每日一题#

简单回答：
y*y=x mod p，已知x，p并且互质，求y。
1.判断是否存在模平方根。
1.1.欧拉判别法。有代码。
x**[(p-1)/2]%p==1。
1.2.高斯二次互反律。无代码。
2.Tonelli–Shanks算法。有代码。

代码用python编写，代码如下：

# -*-coding:utf-8-*-

def quick_power(a, b, p):
    """
    求快速幂。ret = a^b%p。

    Args:
        a: 底数。大于等于0并且是整数。
        b: 指数。大于等于0并且是整数。
        p: 模数。大于0并且是整数。

    Returns:
        返回结果。

    Raises:
        IOError: 无错误。
    """
    a = a % p
    ans = 1
    while b != 0:
        if b & 1:
            ans = (ans * a) % p
        b >>= 1
        a = (a * a) % p
    return ans


def is_have_sqrt_model(x, p):
    """
        是否有模平方根y*y=x mod p，已知x，p，判断是否存在y

        Args:
            x: 大于0并且小于p的整数。
            p: 质数。

        Returns:
            返回结果，true表示有模平方根；false表示没有模平方根。

        Raises:
            IOError: 无错误。
    """
    ret = quick_power(x, (p - 1) // 2, p)
    if ret == 1:
        return True
    else:
        return False


def get_sqrt_model(x, p):
    """
        求模平方根y*y=x mod p，已知x，p求y

        Args:
            x: 大于0并且小于p的整数。
            p: 质数。

        Returns:
            返回结果y。

        Raises:
            IOError: 无错误。
    """
    if is_have_sqrt_model(x, p):
        t = 0
        # p-1=(2^t)*s //s是奇数
        s = p - 1
        while s % 2 == 0:
            s = s // 2
            t = t + 1
        if t == 1:
            ret = quick_power(x, (s + 1) // 2, p)
            return ret, p - ret
        elif t >= 2:
            x_ = quick_power(x, p - 2, p)
            n = 1
            while is_have_sqrt_model(n, p):
                n = n + 1
            b = quick_power(n, s, p)
            ret = quick_power(x, (s + 1) // 2, p)
            t_ = 0
            while t - 1 > 0:
                if quick_power(x_ * ret * ret, 2 ** (t - 2), p) == 1:
                    pass
                else:
                    ret = ret * (b ** (2 ** t_)) % p
                t = t - 1
                t_ = t_ + 1
            return ret, p - ret
        else:
            return -2, -2
    else:
        return -1, -1


if __name__ == "__main__":
    print(is_have_sqrt_model(55, 103))
    print(get_sqrt_model(55, 103))
    print("---------------")
    print(is_have_sqrt_model(186, 401))
    print(get_sqrt_model(186, 401))

　　

执行结果如下：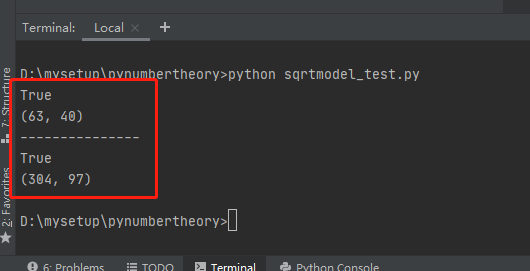

***
[评论](https://user.qzone.qq.com/3182319461/blog/1601854022)