Abstract
本文提出了一种新的方法来寻找不相交k最优路径。最坏情况下计算复杂度为N3log(N)。该方法比WVD算法(https://www.cnblogs.com/walker-lin/p/11051983.html)速度更快。
Introduction
WVD算法中,计算复杂度随着虚警(false alarms)的增加呈指数增加,这限制了算法适用更多的场景。
本文提出的算法are based on a transformation of the K-path trellis problem into an equivalent minimum cost nenvork flow (MCNF) problem。而解决MCNF问题的复杂度随着measurements总数的增加呈多项式增加。
equivalent minimum cost nenvork flow formultion
不相交k最优路径:a)不相交;b)k条路径的总成本最少。
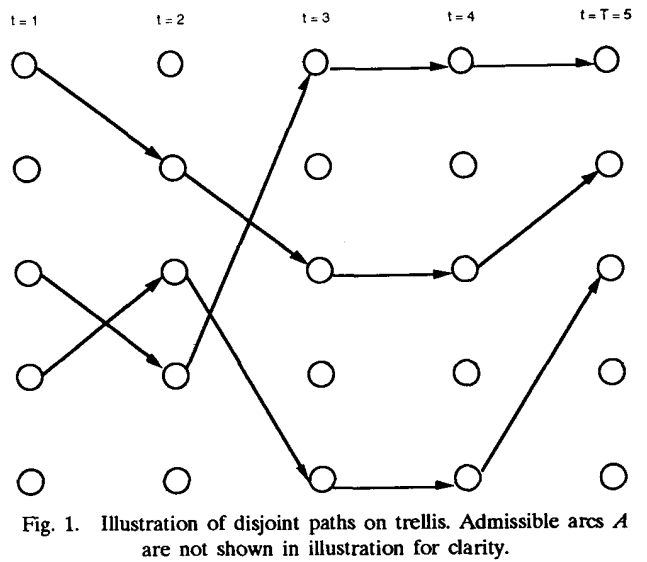
1)如果满足:
a)不要求路径不相交;
b)添加第0层和第T+1层,第0层和第T+1层都只有一个node;第0层到第1层、第T层到第T+1层的arc cost都为0;
c)第0层有K个单位的输入flow,第T+1层有k个单位的输出flow。
则不相交k最优路径问题 → MCNF问题:
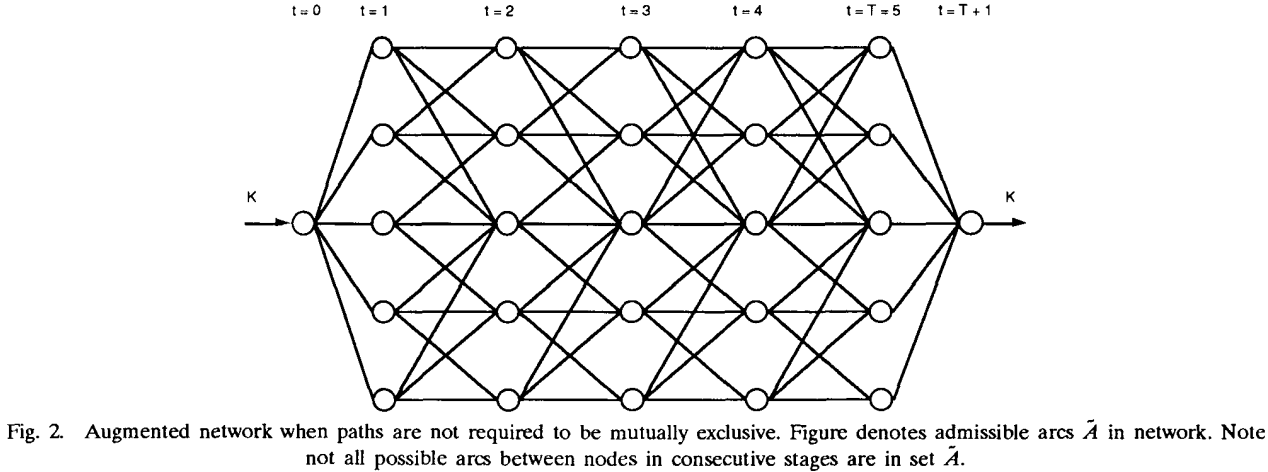
此时,k最优路径(不要求不相交)转换为:
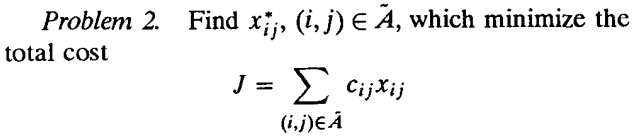

其中,xij表示arc flow,cij表示arc cost。
2)为了满足不相交约束,for each set Nt,t = 2,...,T- 1, 对每一个node添加一个对应node*,且node到node*的arc cost等于0,
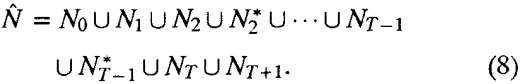
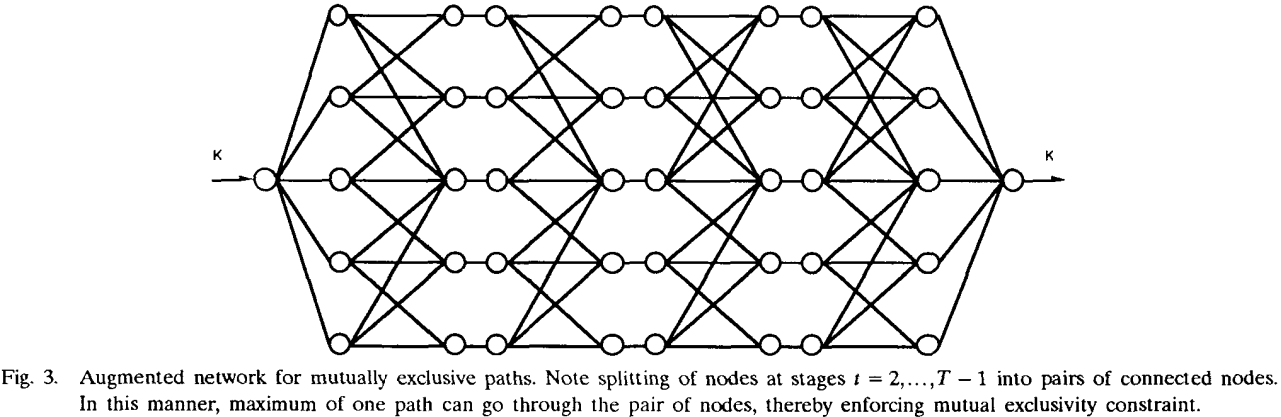
那么,不相交k最优路径可以转换为以下问题:
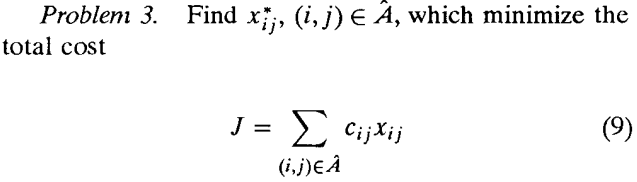

nt中的node最多被使用一次。
算法性能比较
假设Nt=M,t=1,2,......,T。
算法1:WVD算法;算法2:ε-relaxation algorithm in [Dual coordinate step methods for linear network flow problems]。
计算法复杂度:
算法1:O(W),其中![]() ;
;
算法2:![]() ,其中C是cij的最大值。
,其中C是cij的最大值。
空间复杂度:
算法1:O(V),其中![]() ;
;
算法2:O(M2T)