首先用训练好的模型得到所有测试样本的confidence score,每一类(如car)的confidence score保存到一个文件中(如comp1_cls_test_car.txt)。假设共有20个测试样本,每个的id,confidence score和ground truth label如下:
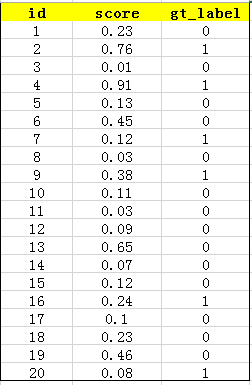
接下来对confidence score排序,得到:

然后计算precision和recall,这两个标准的定义如下:
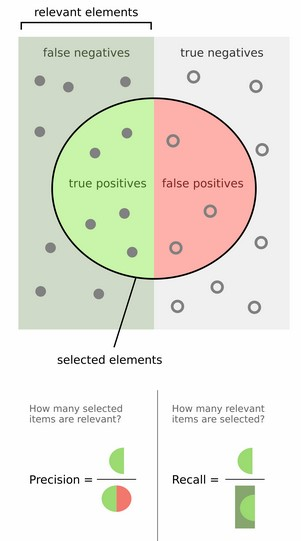
圆圈内(true positives + false positives)是我们选出的元素,它对应于分类任务中我们取出的结果,比如对测试样本在训练好的car模型上分类,我们想得到top-5的结果,即:
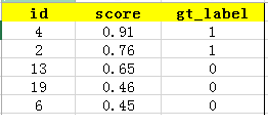
在这个例子中,根据ge_label真实标签,true positives就是指第4和第2张图片,false positives就是指第13,19,6张图片。方框内圆圈外的元素(false negatives和true negatives)是相对于方框内的元素而言,在这个例子中,是指confidence score排在top-5之外的元素,即:
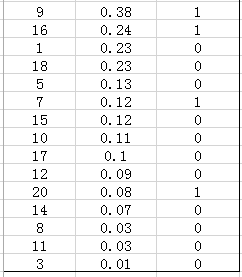
其中,false negatives是指第9,16,7,20张图片,true negatives是指第1,18,5,15,10,17,12,14,8,11,3张图片。
那么,这个例子中Precision=2/5=40%,意思是对于car这一类别,我们选定了5个样本,其中正确的有2个,即准确率为40%;Recall=2/6=30%,意思是在所有测试样本中,共有6个car,但是因为我们只召回了2个,所以召回率为30%。
实际多类别分类任务中,我们通常不满足只通过top-5来衡量一个模型的好坏,而是需要知道从top-1到top-N(N是所有测试样本个数,本文中为20)对应的precision和recall。显然随着我们选定的样本越来也多,recall一定会越来越高,而precision整体上会呈下降趋势。把recall当成横坐标,precision当成纵坐标,即可得到常用的precision-recall曲线。这个例子的precision-recall曲线如下:
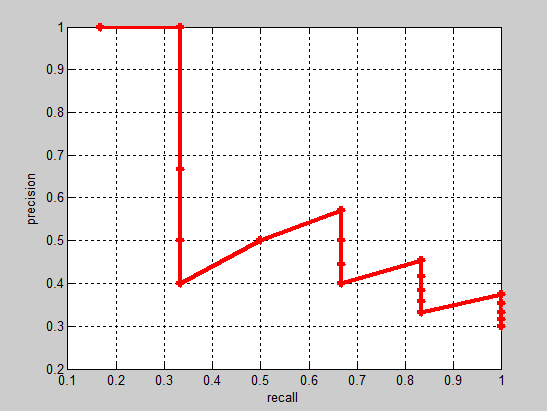
接下来说说AP的计算,此处参考的是PASCAL VOC CHALLENGE的计算方法。首先设定一组阈值,[0, 0.1, 0.2, …, 1]。然后对于recall大于每一个阈值(比如recall>0.3),我们都会得到一个对应的最大precision。这样,我们就计算出了11个precision。AP即为这11个precision的平均值。这种方法英文叫做11-point interpolated average precision。
当然PASCAL VOC CHALLENGE自2010年后就换了另一种计算方法。新的计算方法假设这N个样本中有M个正例,那么我们会得到M个recall值(1/M, 2/M, ..., M/M),对于每个recall值r,我们可以计算出对应(r' > r)的最大precision,然后对这M个precision值取平均即得到最后的AP值。计算方法如下:

相应的Precision-Recall曲线(这条曲线是单调递减的)如下:
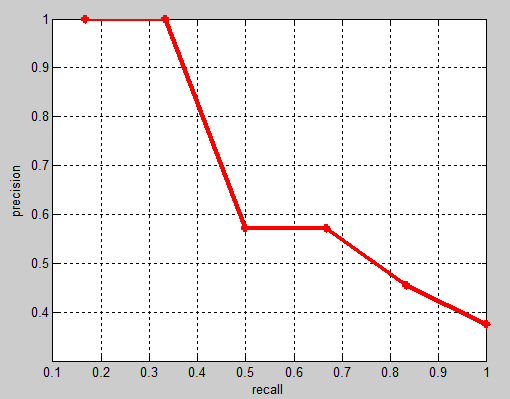
对每个recall对应的precision求均值就得到所谓的average precision,即AP。这样就得到了对应一个类(分类器)的average precision,它表示的是该模型在某个类别上的好坏,如果要求模型在所有类别上的好坏,就求所有类别对应的AP的均值,即所谓的mAP。
参考链接:http://blog.sina.com.cn/s/blog_9db078090102whzw.html