这节主要介绍了生成学习算法。首先与逻辑回归分类算法进行比较,引出生成学习算法的核心思想,然后介绍了一种基本的生成学习算法——高斯判别分析,并进一步对高斯分布条件进行讨论,比较生成学习算法与判别学习算法的区别,最后介绍了两种适合文本分类的朴素贝叶斯方法,并由引入新数据时产生的问题介绍拉普拉斯平滑法。
基本思路是:
- 生成学习算法(Generative Learning Algorithms)
- 高斯判别分析(Gaussian Discriminant Analysis)
- 朴素贝叶斯(Naive Bayes)
- 拉普拉斯平滑(Laplace Smoothing)
一、生成学习算法
判别学习算法,计算条件概率p(y|x;θ),直接学习从特征X到标签y∈{0,1}的映射。如逻辑回归,寻找一条直线(决策边界)将两类数据集分开,新数据落入哪边就属于哪类。
生成学习算法,计算联合概率p(x,y),或者理解为对p(x|y)和p(y)同时进行建模。对不同类别的数据集分别进行建模,看新输入的数据更符合哪类模型,该数据就属于哪类。
Case, 对动物进行分类,y=1表示是大象,y=0表示是小狗,p(x|y=1)是对大象特征建模后的分布,p(x|y=0)是对小狗特征建模后的分布。
结合贝叶斯公式,可以由先验概率p(x|y)和p(y)求出后验概率p(y|x)。

其中,p(x)=p(x|y=1)p(y=1)+p(x|y=0)p(y=0).
二、高斯判别分析
1. 多元正态分布(multivariate normal distribution)
(1)定义:
n维的多元正态分布(多元高斯分布),由参数均值向量μ∈Rn和协方差矩阵Σ∈R(nXn)确定,记作N(μ,Σ),它的概率密度公式为:
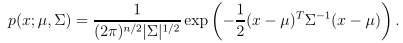
其中,|Σ|为Σ的行列式。
对于随机变量X~N(μ,Σ),它的期望为多元正态分布的均值μ,协方差为其协方差矩阵Σ。
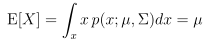
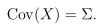
(2)参数:
- 协方差Σ
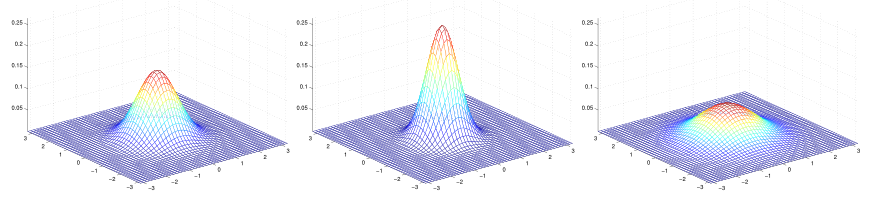
(a)Σ=I (b)Σ=0.6I (c)Σ=2I
(a)中协方差为一个2维的单位矩阵,均值为0,也被叫做标准正态分布。当Σ变大时,高斯分布会变得更加拓展(c);当Σ变小时,高斯分布变得更加压缩(b)。
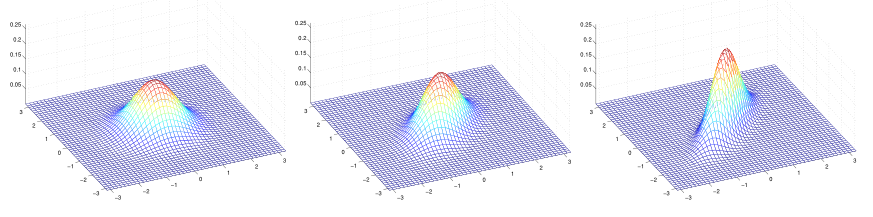
以上三图,均值为0,协方差矩阵Σ分别为:
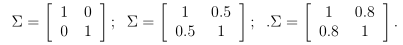
当增加协方差矩阵斜对角线的值,分布沿着45度角的方向压缩,随着它的值增加,压缩得越多。当协方差矩阵斜对角线值减小为负时,分布沿着45度的反方向压缩。
- 均值μ
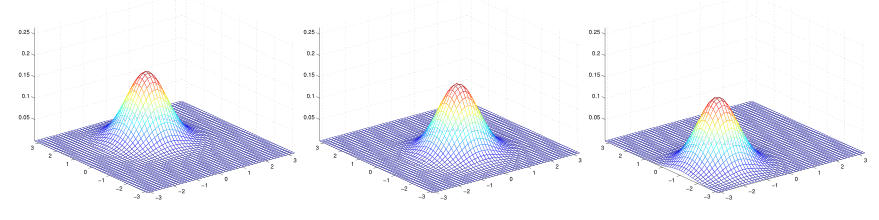
当固定协方差的值,随着均值μ的变化,可以看出,分布的位置随之而变化。
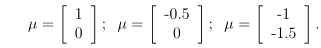
2. 高斯判别分析建模
假设输入x为连续值的随机变量,且满足多元正态分布。
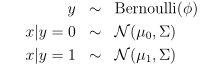
于是,可以得到p(x|y)的表达式。
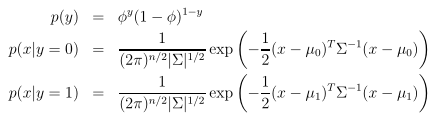
模型的参数为Φ,μ1,μ2,Σ,它的对数似然函数为,这里所求的是联合概率。

最大化对数似然函数,可得各个参数的估计值:
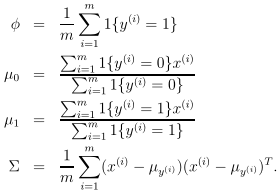
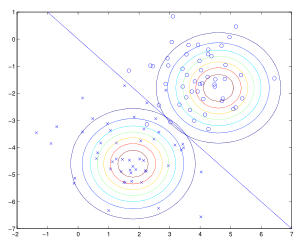
对实际例子进行建模后的等高图如下,两类样本集拥有相同的协方差Σ,故它们的形状是完全相同的,而均值μ不同,所以位置是不同的。图中的直线表示的是p(y=1|x)=0.5的决策边界。
3. 比较GDA和逻辑回归
(1)引例
由于
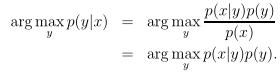
特别地,当p(y)是均值分布,即p(y)对于不同的y值取值都相同,可以继续简写为argmax p(x|y)。也就是说,最终问题可以简化为求p(x|y)。
现在讨论两个一维正态分布的GDA问题,求取p(y=1|x),即为求p(x|y=1)和p(x|y=0)。
观察p(y=1|x),它其实是一个关于x的函数,形状类似Sigmoid函数,可以表示为:
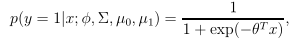
其中,θ是关于Φ,μ1,μ2,Σ的函数。
(2)比较
那么,GDA和逻辑回归哪种分类模型更好呢?
由GDA模型的推导过程可知,当p(x|y)是多元正态分布时,可以推到出p(y|x)满足逻辑函数,而反之不成立。这说明GDA比逻辑回归做了更强的模型假设。
其实,还有很多其他分布条件满足时,可以推导出p(y|x)满足逻辑函数的结论。例如,x|y服从泊松分布:x|y=1~Poisson(λ1),x|y=0~Poisson(λ0),则p(y|x)也是逻辑函数。推广之,x|y=1~ExpFamily(λ1),x|y=0~ExpFamily(λ0),则p(y|x)也是逻辑函数。当把GDA应用在不服从高斯分布却又能推导出逻辑函数的条件下,效果也并不好。
总之,当高斯分布成立或大概成立,模型假设的条件性更强,那么GDA将优于逻辑回归,GDA是渐进有效的(asymptotically efficient)。当若相反的并不知道是否成立时,假设性更弱,逻辑回归会更好,具有更强的鲁棒性。事实上,当未知训练集是否服从高斯分布,且在规模有限时,逻辑回归的表现往往要好于GDA。因此,逻辑回归比GDA要常用。
三、朴素贝叶斯
GDA针对的是连续变量,现在要来说一个针对离散变量的分类模型:朴素贝叶斯。
(1)多元伯努利事件模型(multi-variate Bernoulli event model)
引例,垃圾邮件分类
特征向量x,当邮件中含有词典中的第i个词,则设置xi=1,反之则为xi=0.例如,

假设xi是条件独立的(朴素贝叶斯假设),有50000个词。现在要建立一个生成学习算法,就要计算p(x|y),于是有:
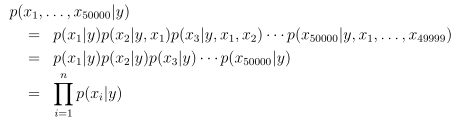
模型参数:
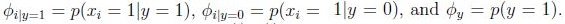
联合似然函数为:
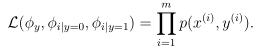
极大似然函数的参数估计为:
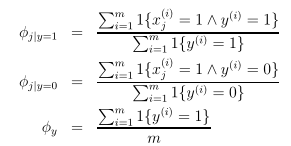
预测一个新的输入x:
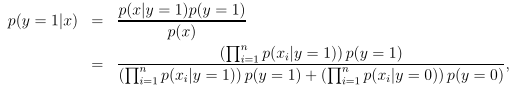
总之,假设xi∈{0,1},y=词典中词的个数,求p(x|y)和p(y)来求后验概率p(y|x)最大。这种模型也叫做多元伯努利事件模型。
针对文本分类,还有另外一种更为有效的模型。
(2)多项式事件模型( multinomial event model)
多元伯努利事件模型中的特征向量缺少某些信息,如不同的词语在邮件中出现的次数。
假设ni=邮件中词的总个数,xj∈{1,2,...,50000},表示对应邮件中第j个位置出现的词,也就是指向词典的索引。
一个邮件的联合概率分布为:
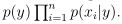
参数为:
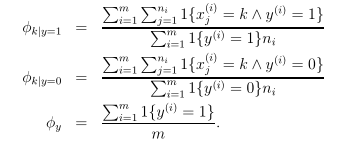
Φk|y=1表示的是在垃圾邮件中词k所占比例。
对数似然性为:
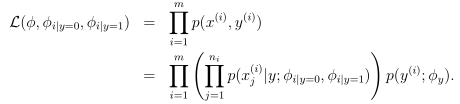
由于考虑了一个文档中词出现的次数,故文本分类效果比第一种朴素贝叶斯的事件模型要好。
(3)存在的问题:
假设有一个未在之前的词典中出现过的新词,它的位置在35000,则参数估计为:
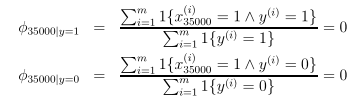
则后验概率为:
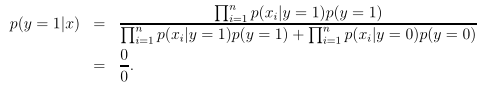
最终得到的是一个不定式,也就是说此时模型无法判断这个新词的分类。为了解决这种问题,引入拉普拉斯平滑。
四、拉普拉斯平滑
朴素贝叶斯的问题出在,Φ的有些极大似然估计值可能取值为0,归根结底,是Φj的分子可能为0导致的。
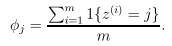
拉普拉斯平滑就是通过增加一些修正因子,分子增加1,分母增加k来优化。
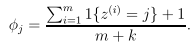
这样做并不改变Φj整体概率仍然为1。
朴素贝叶斯第一种模型的拉普拉斯平滑为:
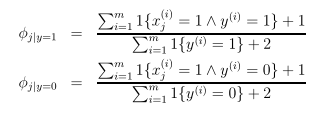
朴素贝叶斯第二种模型的拉普拉斯平滑为:
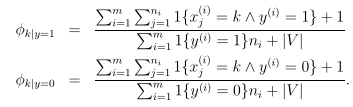
参考文献: