线性表

阅读目录

• 一、线性表的概念和表抽象数据类型
• 二、顺序表的实现
• 三、链接表
• 四、链表的变形和操作
• 五、课后部分编程练习(初学时写的，仅供参考)

一、线性表的概念和表抽象数据类型

1、表的概念和性质

线性表示某类元素的一个集合，记录着元素之间的一种顺序关系。

理解表的下标，空表，表的长度，顺序关系，首元素，尾元素，前驱元素和后继元素等概念。

2、表抽象数据类型

从实现者角度考虑两个问题：

•  如何把该结构内部的数据组织好。
•  如何提供一套有用并且必要的操作。

线性表的操作

•  创建操作。考虑提供初始元素的序列问题。
•  解析操作。判断是否为空，表的长度，取得表内特定数据等。
•  变动操作。添加删除特定元素等。
•  连表操作。两表组合得到新表等。
•  遍历操作。对每个元素进行操作等。

表抽象数据类型

3、线性表的实现

研究数据结构的实现问题，主要考虑两个方面的问题：

•  计算机内存的特点。以及如何保存元素的关系。(隐式还是显式)
•  各种重要操作的效率。

根据上面两个问题，得出两种基本的实现模型：

•  将元素顺序放在一大块的连续存储区内，这样实现的表称之为顺序表。
•  将元素放在通过链接构造起来的一系列存储块中，这样的实现称为链接表。

二、顺序表的实现

顺序表的实现思路很简单，表中的元素顺序放在一片足够大的连续内存中。首元素存入存储区的开始位置，其余元素依次存储。元素之间的关系通过元素在存储区里的物理位置表示(隐式表示元素间的关系)。

1、基本实现方式

• 表里要保存的元素类型相同，因此每个表元素所需的存储量相同，可以根据公式Loc(ei) = Loc(e0) + c * i很快求出元素ei的地址，从而访问到它的元素。
• 表中的元素大小不一。将实际元素另行存储，在顺序表里的各单元保存的是对相应元素的引用信息。这样，通过上面公式计算出引用信息的位置，在通过引用信息访问到元素本身。这样的顺序表也被称为对实际数据的索引。

线性表的一个重要的性质是可以添加删除元素，那么就会带来一个问题，我们在建立一个表时，需要给它分配多大的内存？

一个合理的办法是分配完已有的元素之外，再留一些空位以备添加操作使用。

上图实例是一个顺序表的完整信息。包括容量大小，元素个数，以及各个元素内容。

2、顺序表基本操作的实现

创建和访问操作

• 创建空表，创建空表时，需要分配一块元素存储，记录表的容量并将元素计数值设置为0。
• 简单判断操作。表空或者表满都是O(1)。
• 访问给定下标i的元素。O(1)。计算地址，访问元素。
• 遍历操作。O(n)。
• 查找给定元素d的(第一次出现的)位置，这种操作称为检索或者查找。在没有其他信息的情况下，只能通过用d与表中元素逐个比较的方式实现检索，称为线性检索。O(n)。
• 查找给定元素d在位置k之后的第一次出现的位置。与上面操作类似。O(n)。

最后几个操作都需要检查表元素的内容，属于基于内容的检索。数据存储和检索是一切计算和信息处理的基础。

不修改表结构的操作只有两种模式，一种是直接访问，一种是基于一个整型变量，按照下标循环并检查和处理(也就是变量操作)。

变动操作：加入元素

尾端加入新数据项。把新数据项存入表中的第一个空位，即下标num的位置。如果这个时候表满了，操作就失败。显然这个操作是O(1)。

新数据存入元素存储区的第i个单元。这是一般情况。

首先需要下标是否合法，要把新数据存入这里，又不能简单抛弃原有的数据，就必须把该项数据移走。

移走方式有两种：

• 不需要保持原有的序列，那么只需要把原来处于i位置的元素移到最后面，然后把新元素放到i元素的位置。这种操作能在O(1)时间完成。
• 如果要保持原有的序列，就需要不断把i位置之后的元素逐一后移。这种操作最坏和平均复杂度都是O(n)。python采用这种方法。

变动操作：删除元素

尾端删除数据。将元素计数值num-1，就相当把表尾的元素删除了。O(1)。

删除位置id数据。这个跟加入跟加入操作类似，也是分两种情况。

• 如果没有保序要求，就追吧num-1位置的元素拷贝过去，覆盖掉原来的元素。
• 如果有保序要求，就需要删除原来的元素之后，逐一上移其余元素。显然非保序定位删除操作的时间复杂度是O(1)。而保序定位删除的复杂度是O(n)，因为其中可能会移动一系列元素。

基于条件的删除

这种删除操作并不是给定被删元素的位置，而是给出需要删除的数据项本身。或是一个满足删除的条件。这个显然跟检索有关，需要先找到元素，再删除它。

顺序表及其操作的性质

顺序表的各种访问操作，如果其执行中不需要扫描表内容的全部或者一部分，其时间复杂度都是O(1),需要扫描表内容操作时间复杂度都是O(n)。

顺序表的优点：

•  可以O(1)时间的按位置访问元素。
•  元素在表里的存储紧凑，只需要O(1)空间存放少量辅助信息。

缺点：

• 如果表很大，即需要很大片的连续内存空间。
• 内存一旦确定大小，就不能变化，导致内存利用不合理。
• 在执行一般加入和删除操作的时候，通常需要移动元素，效率低。
• 在建表的初始就需要考虑存储区大小。 

3、顺序表的结构

一个顺序表的完整信息包括两部分，一部分是表中的元素集合，另一部分是为实现正确操作而需要记录的信息(也就是表中的个数和大小等信息)。

两种基本实现方式

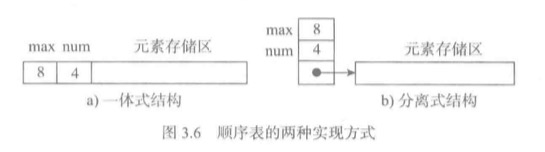
一体式实现，有关信息跟表元素放在一起。

• 优点：比较紧凑，有利于管理。
• 缺点：不同的表对象大小不一。还有就是创建之后元素的存储区就固定了。

分离式实现，在表对象里只保存与整个表有关的信息，实际元素存放在另外一个独立的元素存储区对象里，通过链接与基本表对象关联。

• 优点：表对象大小统一，不同对象关联不同大小的元素存储区。
• 缺点：表的创建和管理，必须考虑多个独立对象。

替换元素存储区

分离式实现的最大优点是可以在标识不变的情况下，为表对象更换一块元素存储区。

操作流程：

1. 另外申请一块更大的元素存储区。
2. 把表中已有的元素复制到新存储区。
3. 用新的元素存储区替代原来的元素存储区(改变表对象的元素区链接)
4. 实际加入新的元素。

人们把利用采用这种技术实现的表称之为动态顺序表。

后端插入和存储区扩充

把一个动态顺序表从0逐渐扩大到n，如果是前端添加，那么整个就是O(n²)复杂度。
如果是从后端添加，一次操作是O(1)的复杂度，不过这里要考虑一个问题，就是元素的替换问题。当整个表满的时候，就会申请一个新的内存复制已有的元素，这个操作是O(m)复杂度，m是当时表中元素的个数。

那么就有一个问题，如果安排初始表中元素的数量，以及它的扩展策略？

很明显，如果一次扩展的多，会造成内存空间的浪费，而如果扩展的不多，那么就会频繁地进行复制替换操作，造成性能下降。

下面用两种不同的扩展策略来说明一下这个问题。

• 线性增长策略。即每次扩展固定数目的元素。假设每次替换增加10个元素。那么，从0到1000总的复制次数是10+20+....+990 = 49500 = 1/20*n的平方,这样即使是单次操作的尾端添加O(1)也会让整个过程变成O(n的平方)。原因就是频繁的替换元素存储区，而且随着元素变多，每次替换复制的元素也越来越多。因此，应该考虑一种策略是随着元素数量的增加，替换存储区的频率不断的降低。
• 加倍操作。每次扩展原元素数据的一倍。假设表元素从0到1024，那么表增长过程中复制元素的次数是1+2+4+8+....+512=1023=log2(下标)1024 -1。这样在整个表增长的过程中，元素的赋值次数也就是O(n)。每次插入操作的平均复杂度是O(1)。

当然，后一个策略也有缺点，比如当元素很多的时候，一次扩展的空间就很大，这样如果用不完，就会造成空间浪费。解决方法，可以两种策略一起使用，另外如果对于高要求的程序，需要增加一个设定容量的操作，当下面的操作需要高要求的时候，就事前把表的容量修改到一个足够大的值，保证在关键计算的时候不会出现替换操作。

4、python中list

list的基本实现技术

python中的list就是一种元素个数可变的线性表，并且添加删除元素后维持原来的顺序。

• 基于下标的高效位置访问和更新。O(1)。
• 允许任意添加元素，不会出现表满的情况，在添加的过程中对象的标识不变。(分离式结构的动态顺序表)。
• 表中的元素保存在一块连续的存储区内。
• 使用加倍策略。初始的时候是8，然后一次替换加4倍。当到达50000的时候，变成加倍策略。

一些主要操作的性质

• len()。O(1)
• 元素访问和赋值。O(1)
• 一般位置添加，删除，切片，extend，pop()非尾端删除，都是O(n)操作。

python的一个问题是没有提供list检查容量的操作，也没有设置容量的操作，所有关于容量的操作都由python解释器自动完成。

• 优点：降低编程人员的负担。
• 缺点：限制了表的使用方式。

其他几个操作

• clear()。O(1)。可以另外分配一个空表，然后更改存储区，等待解释器回收内存块。也可以将表的计数值设置为0，但是这种并没有释放内存。
• reverse()。看下面代码，很容易得出他是O(n)操作。
• sort()。O(nlogn)。具体参考后面章节的排序。

def reverse(self):
    elems = self.elems
    i, j = 0, len(elems)-1
    while i < j:
        elems[i], elems[j] = elems[j], elems[i]
        i, j = i+1, j-1

三、链接表

1、实现链接表的基本思路

实现线性表的另外一种方式就是链接表，它用链接关系显示表示元素之间的顺序关系。这种表也称为链表。

基本思路：

* 把表中元素分别存储在一批独立的存储块(表的结点)中。
* 保证从组成表结构的任一结点可找到与其对应的下一个结点。
* 在前面一个结点里面显示记录下一个结点的链接。

这样只要找到了第一个结点，就能找到所有的结点。

2、实现单链表的操作分析

单链表的结点是一个二元组，它的表元素域elem保存着作为表元素的数据项(或者数据项的关联信息)，链接域next保存同一个表里下一个结点的标识。

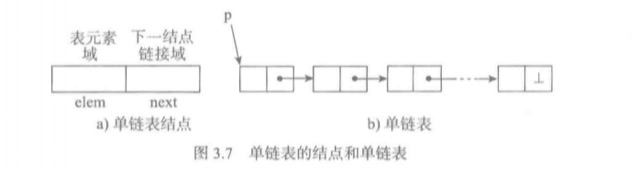
一个单链表不仅要有结点，还需要一个表头指针，这样就可以通过这个指针找到所有表中的节点。这个表头指针最开始指向的是表头节点。

• 一个单链表由一些具体的表结点构成。
• 每个结点是一个对象，有自己的标识。
• 结点之间通过结点链接建立起单向的顺序。

为了表示一个链接的结束，只需要给表的最后结点的链接域设置一个None值。

class LNode:
    def __init__(self, elem, next_=None):
        self.elem = elem
        self.next = next_  #为了不与python的next重名

基本链表操作

• 创建空链表。只需把表头指针设置为空链接，也就是None就可以了。
• 删除链接表。在C里，需要通过明确的操作释放一个个节点所用的存储。在python里，只需要把表指针指向None，python解释器就会回收表结点中不用的存储。
• 判断表是否为空。表指针是否为None。
• 判断表是否满。一般链表不会满，除非存储空间用完。

加入操作

表首端插入

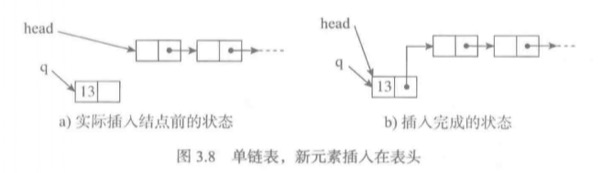
1. 创建一个新结点，并存入数据。
2. 将新结点的引用域(next)设置为原表头。
3. 将表头指针指向新的结点。

可以看出这只需要几个赋值操作，因此复杂度是O(1)。

一般情况的插入

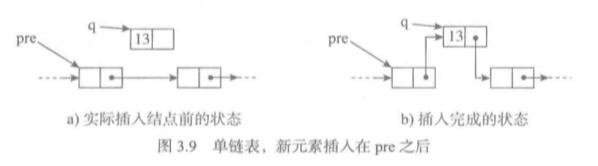
1.  创建一个新结点q，并存入数据。
2.  找到要插入结点的前一个结点pre。这时pre的下一个结点是pre.next
3. 先把新结点q的引用域设置为p以前的下一个结点也即是pre.next。再把pre的引用域(next)设置为新结点q。

这个操作主要是第2步需要找到要插入结点的前一个结点，需要遍历整个链表。因此整个复杂度是O(n)。

删除元素

删除表首元素

让表头指针指向表的第二个元素就可以了。python内存管理器会自动回收表头元素。也就是，self.head = self.head.next。

一般情况的元素删除

一般情况的删除跟一般情况的添加一样，需要找到相关元素。删除的时候，先找到要删除的前一个元素p，然后把它的引用(next)设置为要删除元素的后一个元素。也就是pre.next = pre.next.next

扫描、定位和遍历

在上面不论是一般删除还是一般添加，都需要找到要操作元素的前一个结点。由于单链表只有一个方向，因此，从表头指针开始，做一个循环，就能找到整个链表中的所有结点。这个过程称为链表扫描。

p = head  # 扫描指针
while p is not None and 其他条件:
    对p中的数据做操作
    p = p.next

p = head
while p is not None and i > 0:
    i -= 1
    p = p.next

p = head
while p is not None:
    if elemt == p.elem:
        return 
    p = p.next

链表操作的复杂度

• 创建空表O(1)
• 删除表O(1)
• 判断空表O(1)
• 加入元素，首端加入O(1)，一般加入O(n)。
• 删除表元素，删除表头O(1)，一般删除O(n)。

表的长度

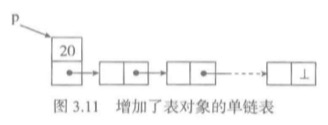
看表的设计，如果设计表时，有表长度len的参数，那么删除，添加元素必须维持这个参数。这时表的长度就是O(1)。只需获得属性值就可以。

如果没有这个参数，每次就长度，就需要遍历链表。O(n)的复杂度。

p = head
i = 0
while p is not None:
    p = p.next
    i += 1 

3、单链表的实现

class LinkedListUnderFlow(ValueError):
    '''
    自定义异常类，为了更快定位是链表中的异常，从而进行处理。
    '''
    pass

class LNode:
    '''
    链表中的节点类
    '''
    def __init__(self, elem, next_=None):
        self.elem = elem
        self.next = next_

class LList:
    '''
    链表的实现
    '''
    def __init__(self):
        slef.head = None   # 表头指针
    
    def empty(self):
        '''
        判断表是否为空表
        '''
        return self.head is None
    
    def prepend(self, elem):
        '''
        在表首端添加元素
        '''
        self.head = LNode(elem, self.head)
    
    def pop(self):
        '''
        删除表头结点并返回删除的元素
        '''
        if self.empty():
            raise LinkedListUnderFlow('in pop')
        e = self.head.elem
        self.head = self.head.next
        return e
    
    def append(self, elem):
        '''
        在表尾添加元素
        '''
        if self.empty():    # 如果表是空的，必须设置表头指针指向新元素
            self.head = LNode(elem)
            return 
        p = self.head   # 扫描指针
        while p.next is not None: # 找到表中的最后一个元素p。
            p = p.next
        p.next = LNode(elem)
    
    def pop_last(self):
        '''
        删除表中的最后一个元素，并返回其所删除的元素
        '''
        if self.empty():
            raise LinkedListUnderFlow('in pop_last')
        if self.head.next is None:  # 表中只有一个元素
            e = self.head.elem
            self.head = None
        else:
            p = self.head
            while p.next.next is not None:  # 找到要删除元素的前一个元素
                p = p.next
            e = p.next.elem  
            p.next = None
        return e
    
    def find(self, pred):
        '''
        满足条件pred的第一个元素
        '''
        p = self.head
        while p is not None
            if pred(p.elem):
                return p.elem
            p = p.next
    
    def print_all(self):
        '''
        打印链表中所有的元素，以，分隔开
        '''
        p = self.head
        while p is not None:
            print(p.elem, end='')
            if p.next is not None:
                print(',', end='')
            p = p.next
        print('')  # 只是为了输出一个换行符
        
    def for_each(self, proc):
        '''
        对每个元素做一个指定的操作函数
        '''
        p = self.head
        while p is not None:
            proc(p.elem)
            p = p.next
    
    def elements(self):
        '''
        遍历这个链表，使用迭代器
        '''
        p = self.head
        while p is not None:
            yiel p.elem
            p = p.next
    
    def filter(self, pred):
        '''
        满足条件pred的所有元素
        '''
        p = self.head
        while p is not None:
            if pred(p.elem):
                yiel p.elem
            p = p.next

四、链表的变形和操作

1、单链表的简单变形

前面的单链表有一个缺点，如果要从尾端加入元素的话，必须要先找到最后一个元素，这样复杂度就成为了O(n)。

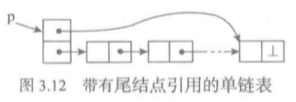
可以通过给表增加一个尾结点的引用域，也就是尾指针，这样就可以在O(1)的时间找到尾元素，从而达到O(1)的复杂度。

新的表除了尾部添加功能，跟尾部删除功能，以及与尾指针有关的操作不一样外，其他的操作跟单链表一样，因此，可以选择继承这个单链表。

class LList1(LList):
    def __init__(self):
        super().__init__()
        self.rear = None
    
    def prepend(self, elem):
        '''
        首端添加，注意，当为空表的时候，必须设置尾指针。
        '''
        if self.empty():
            self.head = LNode(elem)
            self.rear = self.head
            return
        self.head = LNode(elem, self.head)
    
    def append(self, elem):
        '''
        尾端添加，可以达到O(1)的复杂度，因为不用循环表去找最后一个结点了。通过尾指针就可以直接找到。这个设计跟前面求表长的设计一样，都是通过一个维持一个属性值的正确性，来减少遍历的操作
        '''
        if self.empty():
            self.head = LNode(elem)
            self.rear = self.head
            return 
        self.rear.next = LNode(elem) #将新结点放入尾结点的next引用域，使之与链表串起来
        self.rear = self.rear.next  #将尾指针指向链表
    
    def pop_last(self):
        '''
        尾端删除，还是O(n)的复杂度，因为尾指针只能找到最后一个结点，而尾端删除需要找到最后一个结点的前一个结点。因此还需要循环一遍表，唯一与前面不同的地方是，删除的时候需要维护尾指针。
        '''
        if self.empty():
            raise LinkedListUnderFlow('in pop_last')
        if self.head.next is None:
            e = self.head.elem
            self.head = self.rear = None  # 这一步也可以直接写成self.head = None,因为判断表是否为空是用首指针来判断的。只要手指针为空就确定这个表没有元素了。
        else:
            p = self.head
            while p.next.next is not None:
                p = p.next
            e = p.next.elem
            p.next = None
            slef.rear = p
        return e
        

首端删除跟前面单链表是一样的，只要首指针指向None就说明表空，因此在首端删除的时候，并不需要维护尾指针。

表设计的内在一致性

就是在一个类内部，如果其他条件不变，设计原则尽量保持统一。

def prepend(self, elem):
        '''
        这是从首端添加的另一个版本，虽然代码肯定正确，而且代码量还少，但是它有一个不好的地方，就是判断表空的时候使用的尾指针，这就违背了表设计的内置一致性的原则。不值得推荐。因为在这个类的其他方法中，检查表空都是用的首指针。
        '''
        self.head = LNode(elem, self.head)
        if self.rear is None:  # 判断是空表
            self.rear = self.head

2、循环单链表

单链表的另外一个变形是循环单链表，其中最后一个结点的next域不是指向None，而是指向表的第一个结点。这样就只需要一个表尾指针就可以了。

循环链表与普通链表的不同之处就是在于表循环结束的控制条件。其他，就是尾指针的维护，大体思路跟链表是一样的。

class LCList:
    def __init__(self):
        self.rear = None
    
    def empty(self):
        return self.rear is None
        
    def prepend(self, elem):
        '''
        前端插入元素
        '''
        if self.empty():
            self.rear = LNode(elem)
            self.rear.next = self.rear  # 建立一个结点的自循环
        else:
            self.rear.next = LNode(elem, self.rear.next)
    
    def append(self, elem):
        '''
        后端插入元素
        '''
        self.prepend(elem)
        self.rear = self.rear.next
    
    def pop(self):
        '''
        前端删除元素
        '''
        if self.empty():
            raise LinkedListUnderFlow('in LCList pop')
        if self.rear.next is sel.rear:
            e = self.rear.elem
            self.rear = None
        else:
            e = self.rear.next.elem  # 前端的元素
            self.rear.next = self.rear.next.next
        return e
    
    def print_all(self):
        '''
        打印整个循环链表
        '''
        if self.empty():
            return 
        p = self.rear.next
        while p is not self.rear:
            print(p.elem, end=',')
            p = p.next
        print(p.elem)

3、双链表

单链表只能支持一个方向的扫描和逐步操作，因此它不能达到O(1)的尾部删除时间复杂度。如果希望两端插入和删除操作都能高效完成，就需要两个方向都能扫描，这样要在结点中增加一个向前的引用域。然后，通过尾指针向前一步，就很容易找到这个要删除尾结点的前一个元素。

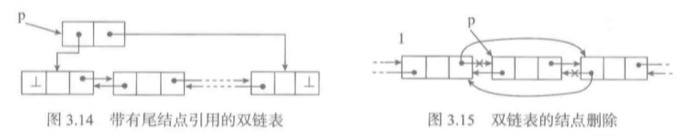
class DLNode(LNode):
    def __init__(self, elem, prev=None, next_=None)
        super().__init__(elem, next_)
        self.prev = prev

class DLList(LList1):
    '''
    继承带有尾指针的单链表
    '''
    def __init__(self):
        super().__init__()
    
    def prepend(self, elem):
        '''
        首端添加
        需要维护结点的引用域prev，因此需要改写
        '''
        if self.empty():
            self.head = DLNode(elem)
            self.rear = self.head
        else:
            self.head.prev = DLNode(elem, next_=self.head)  #将原来首结点的prev域设置为新结点。并将新结点的next域设置为原来的首结点
            self.head = self.head.prev  #将首指针指向新结点
    
    def append(self, elem):
        '''
        尾端添加
        '''
        if self.empty():
            self.head = DLNode(elem)
            self.rear = self.head
        else:
            self.rear.next = DLNode(elem, prev=self.rear)
            self.rear = self.rear.next
    
    def pop(self):
        '''
        首端删除
        '''
        if self.empty():
            raise LinkedListUnderFlow('in DLList pop')
        e = self.head.elem
        if self.head.next is None:
            self.head = None
        else:
            self.head.next.prev = None  # 将第二个元素的prev引用域改为None
            self.head = self.head.next  # 将首指针指向第二个元素
            
        return e
    
    def pop_last(self):
        '''
        这个是O(1)操作，是经过了改良之后有着好性能的方法
        '''
        if self.empty():
            raise LinkedListUnderFlow('in DLList pop_last')
        e = self.rear.elem  # 最后一个结点元素
        if self.head.next is None:
            self.head = None
        else:
            self.rear.prev.next = None # 将最后一个结点的前一个元素的next引用域设置为None。
            self.rear = self.rear.prev
        return e    

循环双链表

双链表也可以定义为循环链表。如下图

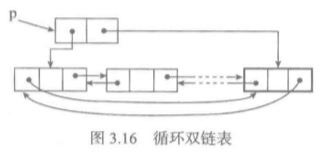
4、两个链表操作

链表反转

先回忆list的reverse，用两个下标，通过逐对交换元素位置，直到两个下标碰头，来完成反转操作。

同样的思路也可以用在双链表上。

def reverse(self):
    '''
    双链表反转的方法，采用搬动元素的思路。
    '''
    i = self.head
    j = self.rear
    while i.prev is not j:  # 当它的i超过j的时候终止循环，完成反转
        i.elem, j.elem = j.elem, i.elem
        i = i.next
        j = j.prev

上面的反转双链表的思路跟反转list的思路是一样的，都是搬动结点的元素。这种思路应用在单链表上也可以完成，但是复杂度O(n²)比较高，因为没有从后向前的方向指针。

因此，这里考虑另外一种反转链表的思路，那就是更改链表的引用域。通过改变结点的链接顺序来改变表元素的顺序。

基本思路：从一个表的首端不断取下结点，将其加入另一个表的首端，这样就完成了一个反转过程。

def reverse(self):
    '''
    单链表反转的方法，采用更改引用域的思路。O(n)的复杂度
    '''
    if self.empty():
        return
    p = None
    while self.head is not None:
        q = slef.head  # 不断拿到首结点
        self.head = q.next  # 将首指针往后移动
        q.next = p   # 更改它的next域，使之指向下一个拿到的首结点
        p = q
    self.head = p

链表排序

先对list的插入排序了解一下，后面有详细介绍。也可以直接看第9章排序的插入排序部分。

def insert_sort(lst):
    for i in range(1, len(lst)):
        tmp = lst[i]  # 找到无序区的第一个元素，把它插入有序区合适的地方
        j = i
        while j > 0 and lst[j-1] > tmp: #如果超出下标或者找到要插入的位置，循环结束
            lst[j] = lst[j-1] # 将比较大的元素逐一后移
            j -= 1
        lst[j] = tmp # 将元素插入找的那个位置
    return lst

使用插入排序的思路和移动链表元素的思路对链表进行排序。与顺序表的插入排序不同是，它寻找要插入的位置不同。顺序表是从右往左移动寻找，而单链表由于只有一个方向，从左往右移动，因此它是从左往右移动去寻找。当找到位置之后，再用一个临时变量保序原位置的elem。以便后来循环插入使用。

def sort1(self):
    '''
    使用插入排序移动元素的思路对单链表进行排序
    '''
    if slef.empty():
        return
    p = self.head.next
    while p is not None:
        e = p.elem # 无序区的第一个元素
        q = self.head 
        while q is not p and q.elem <= e: # 从前往后找到要插入元素的节点位置
            q = q.next
        while q is not p:  # 找到位置，倒腾元素逐一后移
            tmp = q.elem  # 将q位置的元素先存起来
            q.elem = e  # 然后将e位置元素放到q位置
            e = tmp    # 将e的元素更换为以前q位置的元素，以备下次循环替换
            q = q.next
        q.elem = e  # 将最后一个元素回填
        p = p.next

第二种单链表插入排序的实现方法，调整链表的引用域来完成。

def sort2(self):
    '''
    使用插入排序移动元素的思路对单链表进行排序
    '''
    p = self.head
    if p is None or p.next is None:
        return
    rem = p.next  # 取得无序区的第一个元素
    p.next = None    # 将首元素的next引用域设置为None，因为反转之后它就变成最后一个元素了。
    while rem is not None:
        p = self.head
        q = None
        while p is not None and p.elem <= rem.elem:
            q = p
            p = p.next
        if q is None:
            self.head = rem
        else:
            q.next = rem
        q = rem
        rem = rem.next
        p.next = p

 五、课后部分编程练习

# 给链表添加本章开始定义的线性抽象数据类型中没有的操作。
class LList:
    def __len__(self):
        p = self._head
        e = 0
        while p is not None:
            e += 1
            p = p.next
        return e
            
    def insert(self, elem, i):
        if i < 0 or i > len(self):
            raise LinkedListUnderFlow
        elif i == 0:
            self.prepend(elem)
        else:
            p = self._head
            while p is not None and i > 1:
                i -= 1
                p = p.next
            p.next = LNode(elem, p.next)

    def delt(self, i):
        if i < 0 or i >= len(self) or self._head is None:
            raise LinkedListUnderFlow
        elif i == 0:
            self.pop()
        else:
            p = self._head
            while p is not None and i > 1:
                i -= 1
                p = p.next
            p.next = p.next.next

    def search(self, elem):
        p = self._head
        e = 0
        while p is not None:
            if p.elem == elem:
                return e
            e += 1
            p = p.next
        return -1

            

# 请为Llist类增加定位插入和删除操作。
# 答案：见上面第一题

"""
给Llist增加一个元素计数值域num，并修改类中操作，维护这个计数值。
另外定义有一个求表中元素个数的len函数。
请比较这种实现和原来没有元素计数值域的实现，
个说明其优缺点。
"""

#答案：
#这个实现很简单，就是在
def __init__(self):
    self._head = None
    self._num = 0
#初始化计数值为0。
#然后在进行加入元素操作的时候，比如prepend,append,insert等方法中，令self._num += 1
#在删除元素操作的时候，比如pop,pop_last,delt等方法中，令self._num -= 1
#最后写一个len方法。
def len(self):
    return self._num
#这样做的好处是可以在O(1)时间内得到链表的个数，而原来是O(n)时间。
#因此代码执行效率大大提高了。
#但是它的缺点是要实时维护一个计数变量num。

"""
课后练习第四题
请基于元素相等操作'=='定义一个单链表的相等比较函数。
另请基于字典序的概念，为链接表定义大于、小于、大于等于和小于等于判断。
"""
class LList:

    def __init__(self):
        self._head = None
 # ==
    def __eq__(self, other):
        if not isinstance(other, LList):
            raise TypeError
        p, q = self._head, other.head()
        while (p is not None) and (q is not None):
            if p.elem == q.elem:
                p, q = p.next, q.next
            else:
                return False
        if (p and q) is not None:
            return False
        return True

    # <
    def __lt__(self, other):
        if not isinstance(other, LList):
            raise TypeError
        p, q = self._head, other.head()
        while (p is not None) and (q is not None):
            if p.elem < q.elem:
                return True
            elif p.elem == q.elem:
                p, q = p.next, q.next
            else:
                return False
        if (p is None) and (q is not None):
            return True
        return False

    # >
    def __gt__(self, other):
        if not isinstance(other, LList):
            raise TypeError
        p, q = self._head, other.head()
        while (p is not None) and (q is not None):
            if p.elem > q.elem:
                return True
            elif p.elem == q.elem:
                p, q = p.next, q.next
            else:
                return False
        if (p is not None) and (q is None):
            return True
        return False

    # <=
    def __le__(self, other):
        if not isinstance(other, LList):
            raise TypeError
        p, q = self._head, other.head()
        while (p is not None) and (q is not None):
            if p.elem < q.elem:
                return True
            elif p.elem == q.elem:
                p, q = p.next, q.next
            else:
                return False
        if (p is not None) and (q is None):
            return False
        return True

    # >=
    def __ge__(self, other):
        if not isinstance(other, LList):
            raise TypeError
        p, q = self._head, other.head()
        while (p is not None) and (q is not None):
            if p.elem > q.elem:
                return True
            elif p.elem == q.elem:
                p, q = p.next, q.next
            else:
                return False
        if (p is None) and (q is not None):
            return False
        return True

"""
请为链接表定义一个方法，它基于顺序表参数构造一个链接表，
另请定义一个函数，它从一个链接表构造出一个顺序表
"""
    def list_llist(self, mlist):
        for i in range(len(mlist)-1, -1, -1):
            self.prepend(mlist[i])

    def llist_list(self):
        return [i for i in self.elements()]

"""
请为单链表类增加一个反向遍历方法rev_visit(self, op),它能从后向前的顺序把操作op逐个作用于表元素。你定义的方法在整个遍历中访问点的次数与表长度n是什么关系？
如果不是线性关系，请设法修改，使之达到线性关系。这里要求遍历方法的空间代价是O(1)
提示：
你可以考虑为了遍历而修改表的结构，只要能在遍历的最后将表的结构复原。
"""
        
    def rev_visit(self, op):
        self.reverse()
        self.for_each(op)
        self.reverse()

"""
请为单链表类定义下面几个元素删除方法，并保持其他元素的相对顺序
1、del_minimal() 删除当时链表中的最小元素
2、del_if(pred) 删除当前链表里所有满足谓词函数pred的元素
3、del_duplicate()删除表中所有重复出现的元素。也就是说，表中任何元素的第一次出现保留不动，
后续与之相等的元素都删除
要求所有的操作，复杂度均为O(n)
"""

    def del_minimal(self):
        if self._head is None:
            raise LinkedListUnderFlow
        p = self._head
        min_num = p.elem
        while p.next is not None:
            if min_num > p.next.elem:
                min_num = p.next.elem
            p = p.next

        p = self._head
        q = None
        while p is not None:
            if not q and p.elem == min_num:
                self._head = self._head.next
                q = self._head
            elif p.elem == min_num:
                q.next = p.next
                if p.next is None:
                    return
            else:
                q = p
            p = p.next

    def del_if(self, pred):
        """"
        这种方法比较复杂，不能达到O(n)的复杂度要求
        """
        # p = self._head
        # index, i = [],0
        # while p is not None:
        #     if pred(p.elem):
        #         index.append(i)
        #     p = p.next
        #     i += 1
        #
        # print(index)
        # for j in range(len(index)-1,-1,-1):
        #     self.delt(index[j])
        # return index
        p = self._head
        q = None
        while p is not None:
            if not q and pred(p.elem):
                self._head = self._head.next
                q = self._head
            elif pred(p.elem):
                q.next = p.next
                if p.next is None:
                    return
            else:
                q = p
            p = p.next

    def del_duplicate(self):
        p = self._head
        mlist = []
        q = None
        while p is not None:
            if p.elem not in mlist:
                mlist.append(p.elem)
                q = p
            else:
                q.next = p.next
                if p.next is None:
                    return
            p = p.next