栈和队列

目录

• 一、概述
• 二、栈:概念和实现
• 三、栈的应用
• 四、队列
• 五、迷宫求解和状态空间搜索
• 六、补充
• 七、部分课后编程练习

一、概述

栈跟队列都是保存数据的容器。还有前面的线性表。

栈和队列主要用于计算过程中保存的临时数据，如果数据在编程时就可以确定，那么使用几个变量就可以临时存储，但是如果存储的数据项数不能确定，就需要复杂的存储机制。这样的存储机制称为缓存。栈和队列就是使用最多的缓存结构。

1、栈、队列和数据使用顺序

栈和队列是最简单的缓存结构，它们只支持数据项的存储和访问，不支持数据项之间的任何关系。因此，它们最重要的两个操作就是存入元素和取出元素。

当然还有其他的操作，比如创建，检查空(或者满)的操作。

按照数据在时间上生成的先后顺序进行不同的处理：

• 后生成的数据需要先处理。就需要先进后出的数据结构进行存储(栈，Last In First Out)。
• 先生成的数据需要先处理。就需要先进先出的数据结构进行存储(队列，First In First Out)。

那么如何实现这两种结构呢，最自然跟最简单的实现方式就是使用线性表。

2、应用环境

很多，从略。python中可以直接使用list实现栈的功能。可以使用deque，实现队列的功能。

二、栈:概念和实现

存入栈中的元素之间没有任何具体关系，只有到来的时间先后顺序。因此，就没有元素的位置和元素的前后顺序等概念。

栈的基本性质保证，在任何时刻可以访问、删除的元素都是在此之前最后存入的那个元素。

1、栈抽象数据对象

栈的线性表实现相关问题

在线性表的一端进行插入和删除操作，这一端称为栈顶，另一端称为栈底。

对于顺序表，后端插入和删除是O(1)操作，因此考虑使用这一端作为栈顶。

对于链接表，前端插入和删除是O(1)操作，因此用这端作为栈顶。

2、栈的顺序实现

把list直接当做栈使用，也是可以的，只是这样的对象跟list无法区分，并且提供了栈不应该支持的list所有操作，这样就会威胁到栈的安全。

class StackUnderFlow(ValueError):
    '''
    栈下溢，也就是空栈访问
    '''
    pass

class SStack:
    def __init__(self):
        self.elems = []
    
    def is_empty(self):
        return self.elems == []
    
    def push(self, elem):
        self.elems.append(elem)
    
    def pop(self):
        if self.is_empty():
            rasise StackUnderFlow('in SStack pop')
        return self.elems.pop()
    
    def top(self):
        if self.is_empty():
            raise StackUnderFlow('in SStack top')
        return self.elems[-1]

3、栈的链接表实现

顺序表实现的优缺点：

• 优点：表元素放在一个连续的存储块内，方便管理。
• 缺点：当扩大内存的时候，需要一次复制操作，这是一次高代价的操作。

采用链接表实现的优点，不需要一个连续的存储块就可以，而且没有替换存储的高代价操作。但是它的缺点零散的存储比较依赖python的存储管理，还有每个结点的链接也会带来开销。

class LStack:
    def __init__(self):
        self.top = None
    
    def is_empty(self):
        return self.top is None
    
    def push(self, elem):
        self.top = LNode(elem, slef.top)
    
    def pop(self):
        if self.is_empty():
            raise StackUnderFlow('in LStack pop')
        e = self.top.elem
        self.top = self.top.next
        return e
    
    def top(self):
        if self.is_empty():
            raise StackUnderFlow('in LStack top')
        return self.top.elem

三、栈的应用

栈的用途主要是两方面：

• 作为程序中的辅助结构，用于保存需要前进后出的数据。
• 利用栈的先进后出的性质，做一些特定的事情。

s1 = SStack()
for i in list1:
    s1.push(i)
list2 = []
while not s1.is_empty():
    list2.append(s1.pop())

1、简单应用：括号匹配问题

问题：

• 考虑python程序中的括号匹配，这里只考虑三种括号，(){}[]。
• 每种括号都包括一个开括号和一个闭括号，相互对应。
• 对于括号里面的嵌套，也要正确匹配。

分析：

• 由于程序中无法预知要处理的括号数量，因此不能使用固定的变量来进行保存，必须使用缓存结构。
• 需要存储的开括号的使用原则是后存入先使用，符合LIFO原则。
• 如果一个开括号完成配对，就删除这个括号。

实现过程：

• 顺序扫描检查正文里的一个个字符。
• 检查的时候跳过无关的字符
• 遇到开括号将其压入栈中
• 遇到闭括号，弹出栈顶元素与之配对。
• 如果匹配成功继续，直到正文结束。
• 不过不匹配，以检查失败结束。

def check_parens(text):
    '''
    括号配对检查函数，text是被检查的正文串
    '''
    one_parens = '[{('
    opposite = {']':'[',')':'(','}':'{'}
    
    st = SStack()
    for s in text:
        if s in one_parens:
            st.push(s)
        if s in opposite and st.pop() != opposite[s]:
            return False
    if st.is_empty():  #书中没有最后这一步的判断。
        return True
    else:
        return False

2、表达式的表示，计算和变换

表达式和计算的描述

我们常用的表达式是用二元运算符连接起来的中缀表达式。例如：(1+2)*3

中缀表达式是习惯的表达式，但是它有一些缺点，比如不能准确描述计算的顺序，通常需要借助一些辅助符号(比如圆括号)，或者优先级(比如先乘除后加减)。

比如上面的例子中，如果没有()，那么计算顺序将会完全不一样。

因此，当计算机处理表达式的时候，通过会把中缀表达式转化为后缀表达式(逆波兰表达式)。当然，还有一种表达式是前缀表达式(波兰表达式)。

后缀表达式和前缀表达式都不需要括号或者优先级，或者结合性的规定。

例子：

中缀形式：(3-5) * (6+17*4) / 3
前缀形式：/ * - 3 5 + 6 * 17 4 3
后缀形式：3 5 - 6 17 4 * + * 3 /

后缀表达式的计算

分析后缀表达式的计算规则

• 遇到运算对象，把它保存起来。
• 遇到运算符，取出最近保存的两个运算对象，进行运算，将结果保存起来。

遇到问题：

• 使用什么结构保存数据
• 表达式里的元素如何表示(可以字符串)
• 处理失败的情况。

解决方法：

• 使用栈保存数据。
• 表达式的元素使用字符串存储
• 在计算的过程中，如果栈中的元素不足两个，那么操作就失败(说明后缀表达式写的是错误的)。还有，当计算完成之后，栈里最终只能有一个元素(也就是计算的结果)。

为判断不足两个元素的情况，必须给栈添加一个属性(写成方法也可以)，就是栈的深度。

def suffix_exp_evaluator(line):
    '''
    将表达式的字符串变为项的表
    '''
    return suf_exp_evaluator(line.split())
    
class ESStack(SStack):
    @property
    def depth(self):
        return len(self.elems)
    
class suf_exp_evaluator(exp):
    oper = '-+*/'
    st = ESStack()
    
    for x in exp:
        if x not in oper:
            st.push(float(x))
            continue
        
        a = st.pop()
        b = st.pop()
        if x == '+':
            c = a + b
        elif x  == '-':
            c = b - a
        elif x  == '*':
            c = a * b
        elif x == '/':
            c = b / a
        else:
            break
        st.push(c)
        
    if st.depth == 1:
        return st.pop()
    raise SyntaxError('Extra operand(s)')

中缀表达式到后缀表达式的转换

在中缀表达式转换后缀表达式中要注意两点：

• 在扫描中缀表达式的过程中，如果遇到运算对象，就直接将它作为后缀表达式的一个项。
• 把运算符放入后缀表达式要注意送出的时机，必须要处理好优先级和结合性的问题。

infix_operators = '+-*/()'
def tokens(lines):
    '''
    生成器函数，逐一生成line中的一个个项。项是浮点数或者运算符。
    本函数不能处理一元运算符，也不能处理带符号的浮点数。
    '''
    i, llen = 0, len(line)
    while i < llen:
        while i < llen and line[i].isspace():
            i += 1
        if i >= llen:
            break
        if line[i] in infix_operators:
            yield line[i]
            i += 1
            continue
        j = i + 1
        
        while (j < llen and not line[j].isspace() and line[j] not in infix_operators):
            if ((line[j] == 'e' or line[j] == 'E') and j+1 < llen and line[j+1] == '-'):  # 处理负指数
                j += 1
            j += 1
        
        yield line[i:j]
        i = j

def trans_infix_suffix(line):
    st = SStack()
    exp = []

    for x in tokens(line):  # tokens是一个待定义的生成器
        if x not in infix_operators:  # 运算对象直接送出
            exp.append(x)
        elif st.is_empty() or x == '(':  # 左括号进栈
            st.push(x)
        elif x == ')':  # 处理右括号的分支
            while not st.is_empty() and st.top() != '(':
                exp.append(st.pop())
            if st.is_empty():  # 没找到左括号，就是不配对
                raise SyntaxError("Missing '('.")
            st.pop()  # 弹出左括号，右括号也不进栈
        else:  # 处理算术运算符，运算符都看作是左结合
            while (not st.is_empty() and
                   priority[st.top()] >= priority[x]):
                exp.append(st.pop())
            st.push(x)  # 算术运算符进栈

    while not st.is_empty():  # 送出栈里剩下的运算符
        if st.top() == '(':   # 如果还有左括号，就是不配对
            raise SyntaxError("Extra '('.")
        exp.append(st.pop())

    return exp

3、栈与递归

递归满足两个条件：

• 调用自身
• 结束递归的条件

递归调用的过程

以阶乘函数为例：

def fact(n):
    if n == 0:
        return 1
    retrun n * fact(n-1)

看一下fact(3)的计算过程：

• 如果要得到fact(3)的结果，必须先算出fact(2)。
• 在计算fact(3)时参数n是3，在fact(2)时，参数n是2。如此递归下去。
• 那么这个n是不断变化的，因此是需要提前保存的。
• 显然，n的个数不能确定，所以不能使用变量来保存。
• 在这样一系列的递归调用中，n的保存性质符合后进先出的条件，因此需要一个栈来保存与n相关的信息。

我们把这种栈称为程序运行栈。

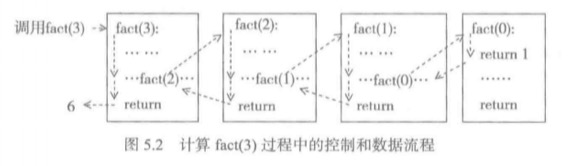
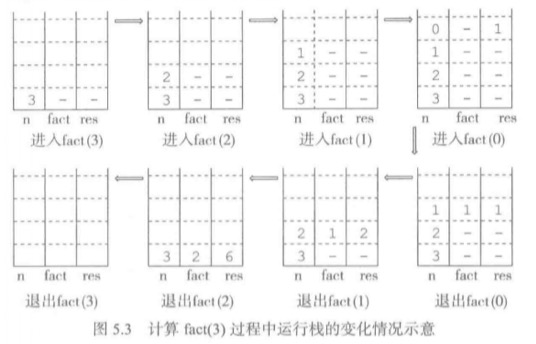
上面两幅图分别描述了fact(3)的调用和返回过程和它的程序运行栈信息变化。

栈和递归/函数调用

一般而言，对于递归函数，其执行的时候都有局部状态，包括函数的形参和局部变量等数据，递归函数在调用自己之前需要先把这些变量保存在程序运行栈中，以备后来使用。

编程语言实现递归函数就是运行一个栈，每个递归函数调用都在栈上开辟一块区域，称为函数帧，用来保存相关信息。位于栈顶的帧是当前帧，所有局部变量都在这里。在进入下一个递归调用时，再建立一个新帧。当函数从下一层递归中返回时，递归函数的上一层执行取得下层函数调用的结果，执行弹出已经结束的对于的帧，然后回到调用前的那一层的执行状态。

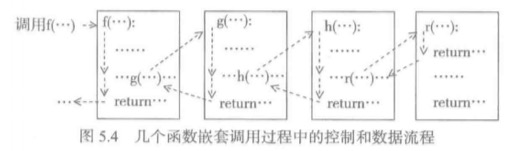
其实不只是递归函数，实际上一般函数的调用和退出的方式也与此类似。例如上图中，在f里调用g，在g中调用h，在h中调用r。也是使用程序运行栈来保存局部数据。

当然，一般函数的调用跟递归函数调用还是有不同的，比如一般函数调用的每个函数局部状态不同，因此，他们的参数个数，局部变量的个数就不同，那么在分配函数帧的容量时就不同。

栈与函数调用*

在程序执行中，函数的嵌套调用是按照‘后调用先返回’的规则进行的，这种规则符合栈的使用模式，因此栈可以很自然的支持函数调用的实现。

函数调用时的内部动作分两部分：

• 新函数调用之前，保存一些信息。(前序动作)
• 退出函数调用时，恢复调用前的状态。(后序动作)

函数的前序动作包括：

• 为被调用函数的局部变量和形式参数分配存储区(函数帧)。
• 将所有实参和函数的返回地址存入函数帧。
• 将控制转到被调用的函数入口。

函数的后序动作包括：

• 将被调用函数的计算结果存入执行位置。
• 释放被调用函数的函数帧。
• 按以前保存的返回地址将控制转回调用函数。

每次函数的调用都要执行这些动作，因此可以看出函数调用是有代价的。

递归与非递归

对于递归函数的调用，实际上就是把信息保存到运行栈中，然后不断执行函数体的那段代码。因此，完全可以修改递归函数，将其变成一个非递归函数。

def norec_fact(n):
    '''
    自己管理栈来模拟函数调用的过程。
    '''
    res = 1
    st = SStack()
    while n > 0:
        st.push(n)
        n -= 1
    while not st.is_empty()：
        res *= st.pop()
    return res

递归函数和非递归函数

任何一个递归函数都可以通过引入一个栈来保存中间结果的方式，翻译为一个非递归函数。同理，任何一个包含循环的程序也可翻译成一个不包含循环的递归函数。

在目前的新型计算机上，函数调用的效率多半都可以接受，通常如果递归的思想比较简单，不一定要用非递归函数定义。当然，除了一些对效率要求特别高的特殊情况之外。

栈的应用：简单背包问题

问题：一个背包可以放重量为w的物品，现在有n件物品，它的集合是S，重量分别是w0,w1,...wn-1。然后，从中挑选出若干件物品，它们的重量之和正好等于w。如果存在，就说这个背包问题有解，如果不存在就无解。

先考虑递归思想的求解思路。
现在用knap(w, n)表示n件物品相对于总总量w的背包问题，那么在通常考虑一件物品选还是不选，有两种情况：

• 如果不选最后一件物品wn-1，那么knap(w, n-1)的解就是knap(w, n)的解，如果找到了前者的解，就找到了后者的解。
• 如果选择最后一件物品，那么knap(w-wn-1, n-1)有解，其解加上最后一件物品就是knap(w, n)的解，也就是前者和后者都有解。

那么n件物品的背包问题就变成了n-1件物品的背包问题。区别就是，一种情况是重量一样，种类减一。一种情况是重量少了，种类减一。

def knap_rec(weight, wlist, n):
    if weight == 0:
        return True
    if weight < 0 or (weight > 0 n < 1):
        return False
    if knap_rec(weight-wlist[n-1], wlist, n-1):
        return True
    if knap_rec(weight, wlist, n-1):
        return True
    else:
        return False

四、队列

1、队列抽象数据类型

2、队列的链接表实现

没有尾指针的实现，如果把链表尾端作为队头，那么加入队列的时间复杂度复杂度是O(n)，而从队列中取出元素的操作(也就是从链表首端删除第一个元素)时间复杂度是O(1)。

如果有尾指针，上面的两个操作都是O(1)的时间复杂度。

具体实现很简单，跟前面的链表类似。

3、队列顺序表实现

基于顺序表实现的问题

利用顺序表现有的结构实现队列：

• 使用顺序表的尾端实现队列的入队操作(append(elem))O(1)，使用顺序表的首端实现队列的出队操作(pop(0))O(n)。
• 使用顺序表的首端实现队列的入队操作(insert(0, elem))O(n)，使用顺序表的尾端实现队列的出队操作(pop())O(n)。

这两种情况都有一个O(n)操作，因此都不理想。

还有一种是在队首出队之后，元素不前移，只需要记住新队头的位置就可以。这个设计虽然能达到O(1)的操作，但是有一个致命的问题，随着不断的入队元素，队列前面会有越来越多的空位，并且这些空位永远不会被利用，这就浪费了存储资源。详情见下图。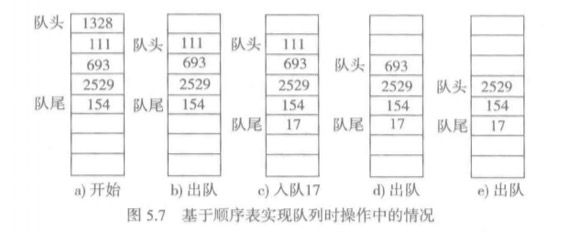

因此，以上的设计都不是最合理的。

循环顺序表

如果把顺序表看做一个环形结构，认为其最后存储位置之后是最前的位置，形成一个环形。那么就会循环利用空间，解决了队首出现空位的情况。

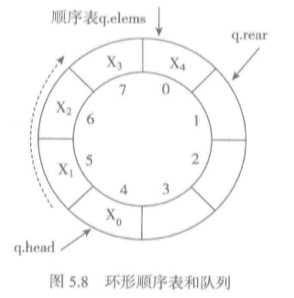
上图是一个包含8个元素的顺序表

• 在队列使用中，顺序表的开始位置并不改变。q.elems始终指向表元素的开始。
• 队头变量q.head记录队列里的第一个元素的位置。q.rear记录当前队列里最后元素的第一个空位。
• 队列元素保存在顺序表的一段连续单元里[q.hear:q.rear]。两个变量之差取模就是队列里元素的个数。

注意变动操作维护上面变量的值，出队和入队时变量更新操作。
q.head = (q.head+1)%q.len
q.rear = (q.rear)%q.len

队空操作。q.head == q.rear
队满操作。(q.rear+1)%q.len = q.head

此外，当队满的时候进行存储空间扩充。这里很难利用list的自动扩充机制，因此需要自己管理list的存储。

4、队列list实现

数据不变式

队列里设计到四个属性,head,rear,num,len。还有一些变动属性的操作。因此，在进行变动操作的时候就应该遵守数据不变式的原则，维护数据的正确性。

数据不变式说明对象的不同属性，描述它们应该满足的逻辑约束关系，如果一个对象的成分取值满足数据不变式，就说明这是一个状态完好的对象。

队列类的实现

class SQueue:
    def __init__(self, init_len=8):
        self.head = 0
        self.num = 0
        self.len = init_len
        self.elems = [0] * self.len
    
    def is_empty(self):
        return self.num == 0
    
    def peek(self):
        if self.is_empty():
            raise ValueError
        return self.elems[(self.head]
    
    def dequeue(self):
        if self.is_empty():
            raise ValueError
        e = self.elems[self.head]
        self.head  = (self.head + 1) % self.len
        self.num -= 1
        return e
    
    def enqueue(self, elem):
        # 表满的时候，需要扩充。
        if self.num == self.len:
            self.extend()
        self.elems[(self.head + self.num)%self.len] = elem
        self.num += 1
    
    def extend(self):
        '''
        表的扩充采用2倍的策略。并且是新表的头是从下边0开始。
        也可以采用新表的头跟原表的下标一样的策略。看设计需求。
        '''
        old_len = self.len
        self.len *= 2
        new_elems = [0] * self.len
        for i in range(old_len):
            new_elems[i] = self.elems[(self.head+i)%old_len]
        self.elems, self.head = new_elems, 0

5、队列的应用

• 文件打印。打印机是文件系统，由于多个进程共享一个文件系统，因此必须使用队列等待一个一个排队打印。
• 万维网服务器。将来不及处理的请求放到一个待请求的队列中。等系统调用。
• windows系统和消息队列。不同进程或者线程通信。
• 离散事件系统模拟。

五、迷宫求解和状态空间搜索

1、迷宫求解：分析和设计

迷宫问题

问题：给定一个迷宫图，包括图中的一个入口点和出口点。要求找到一条从入口到出口的路径。

初步分析：

• 从迷宫的入口开始检查，也就是初始位置开始检查。
• 如果找到出口，问题解决。
• 如果当前方向无路可走，检查失败，需要按照一定方式另外继续搜索。
• 从可行方向中取一个方向继续前进，从那找到出口路径。

迷宫问题分析

分析问题

• 迷宫里面有一集位置，其中有些可以通行的空位置相互直接连通(表现为阵列中邻接的空格，或者矩阵里邻接的0元素)，一步可达。
• 一个空位置有几个相邻元素，也就是几个可能前进的方向。
• 最终目标是找到从入口到出口的一条路径。
• 为找到所需路径，可能更需要逐一探查前进的不同可能性。

这个过程显然需要缓存一些信息：如果当前位置有多个方向可供探查，但是下一步只能探查一个方向，因此需要记录其他暂时不能探查的方向，以后后面使用。

那么该使用什么方式进行缓存呢？

存在两种不同的方式，可以比较冒进，也可以稳扎稳打。

• 如果使用栈的方式缓存，实现的探索过程就是每一步选择一种可能的方向，直到无法前进，退回到此前最后的选择点，更换方向继续探索。也就是所谓的冒进型。
• 如使用队列方式保存，就是总是从最早遇到的索索点不断拓展。也就是稳扎稳打型。

问题表示和辅助结构

迷宫本身使用一个元素值为0/1的矩阵表示，在python中可以用嵌套list表示。迷宫的入口和出口各用一个下标表示。

有一个特殊情况，在探索过程中可能会出现兜圈子的情况，为防止这种情况，必须采用某种方法记录已经探查过的位置信息。

这种位置信息有两种方式表示：

• 使用另外一种专门结构保存这种信息。
• 把已经检查过的信息直接标记在地图上。

现在假设使用一个矩阵表示迷宫图，0表示通路，1表示非通路，2表示已经探查过的路径。

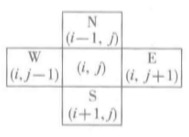
表示当前位置的可行方向。假设用一个二元组表示元素位置(i,j)。i和j分别元素是在矩阵中的下标。那么它的四个方向通过上图就可以表示出来。

此外，还应确定一个位置可探查方向的顺序，在这里规定为‘东南西北’。

2、求解迷宫的算法

迷宫的递归求解

dirs = [(0,1), (1,0), (0,-1), (-1,0)]  #按照东南西北的顺序，给出它与四个方向的差距值。
def mark(maze, pos):
    '''
    用来标记走过的路径。
    '''
    maze[pos[0]][pos[1]] = 2

def passable(maze, pos):
    '''
    检查是否可行
    '''
    return maze[pos[0]][pos[1]] == 0

def find_path(maze, pos, end):
    mark(maze, pos)
    if pos == end:
        print(pos, end=' ')
        return True
    for i in range(4):
        nextp = pos[0]+dirs[i][0], pos[1]+dirs[i][1]
        if passable(maze, nextp):
            if find_path(maze, nextp, end):
                print(pos, end=' ')
                return True
    return False

栈和回溯法

回溯法在工作中执行两种基本动作：前进和后退。

前进：

• 条件：当前位置存在尚未探查的四邻位置。
• 操作：选定下一个位置并向前探查。如果还存在其他可能未探查的分支，就记录相关的信息，以便将来使用。
• 如果找到出口，成功结束。

后退：

• 条件：遇到死路，不存在尚未探查的四邻位置。
• 操作：退回最近记录的那个分支点，检查那里是否有分支，如果有，就取下一个未探查邻位置作为当前位置并前进，没有就将其删除并继续回溯。

def maze_solver(maze, start, end):
    if start == end:
        print(start)
        return 
    st = SStack()
    mark(maze, start)
    st.push((start, 0))  # 0指的是需要从哪个方向开始探索。
    while not st.is_empty():
        pos, nxt = st.pop()
        for i in range(nxt, 4):
            nextp = pos[0] + dirs[i][0], pos[1] + dirs[i][1]
            if nextp == end:
                print(end, pos, st)
                return 
            if passable(maze, nextp):
                st.push((pos, i+1)) # 将原位置和下一个方向存入栈中。
                mark(maze, nextp)
                st.push((nextp, 0))
                break

关于这个算法，有两点说明：

• 发现一个新位置之后，先标记它，然后再将其压入栈中。保证不会兜圈子。
• 一个栈的下一个元素总是到达它路径上的前一个位置，这是搜索中的一个不变性质，保证了栈里的元素构成一条路径。

3、迷宫问题和搜索

其实迷宫问题，是一类问题的代表，这类问题称为状态空间搜索问题。基本特征：

• 存在一集可能状态。
• 有一个初始状态s0，一个或多个结束状态，或者右判断成功结束的方法。
• 对于每个状态s，都有表示与s相邻的一组状态。
• 有一个判断函数valid判断s是否是可行状态。
• 问题:找出从s0触发到达某个结束状态的路径，或者从s0出发，设法找到一个或者全部解。

状态空间搜索:栈和队列

用计算的方法解决问题，根据人们对于问题的认识深度，存在两种不同的处理方法：

• 如果对问题研究比较深入，可以做出一个专门的算法用来解决问题。
• 但更多的情况是对问题认识不够全面，这样就有可能把该问题转化成一个状态空间的搜索问题。

搜索法就是一种通用问题的求解方法。但是在搜索的过程中需要缓存一些已知信息，原则上栈跟队列都可以使用，但是不同的选择，会对搜索进展方式有不同的影响。

在前面的迷宫算法里使用的是栈，它的特点是后进先出，因此会产生回溯。

如果使用队列作为缓存，那么实际上是一种从各种可能齐头并进的搜索。这个过程中没有回溯，只是一种逐步扩张的过程。

基于队列的迷宫求解算法

def maze_solver_queue(maze, start, end):
    if start == end:
        return 
    
    qu = SQueue()
    mark(maze, start)
    qu.enqueue(start)
    while not qu.is_empty():
        pos = qu.dequeue()
        for i in range(4):
            nextp = pos[0] + dirs[i][0], pos[1] + dirs[i][1]
            
            if passable(maze, nextp):
                if nextp == end:
                    print('Path find')
                    return
                mark(maze, nextp)
                qu.enqueue(nextp)

上面的算法有一个问题没有解决，就是找到的路径没有存储。如果想只要找到一条路径，必须另行记录与路径有关的信息。可以考虑使用字典结构实现

def maze_solver_queue(maze, start, end):
    if start == end:
        return 
    
    qu = SQueue()
    mark(maze, start)
    dic = {}
    qu.enqueue(start)
    while not qu.is_empty():
        pos = qu.dequeue()
        for i in range(4):
            nextp = pos[0] + dirs[i][0], pos[1] + dirs[i][1]
            
            if passable(maze, nextp):
                dic[nextp] = pos  # 记录搜索过程中的对象关系key是后一元素，value是前一个元素
                if nextp == end:
                    # 根据记录关系，从后往前推，找到路径
                    p = end
                    while p != start:
                        p = dic[p]
                        print(p)
                    return
                mark(maze, nextp)
                qu.enqueue(nextp)

基于栈和队列的搜索过程

上图中分别是迷宫示例中基于栈和队列的两种不同的搜索路径图。其中栈的特点是，先找一个方向，直到不能再继续的时候，返回最近的那个分叉处，继续探索。因此它是深度优先的搜索。

队列的特点是一步一步搜索，如果有通路就进行前一步探索，不会出现回溯现象。因此它是宽度优先的搜索。

深度和宽度优先搜索的性质

• 假设搜索问题有解，能否保证找到解。深度优先总是沿着一条路径前行，如果存在无穷多的状态无解区域，那么即是其他地方有解，深度优先算法也有可能找不到。宽度优先的算法是这样的，它是从近到远进行扫荡，只要存在到达解的有穷长路径，这种算法就能找到最优解(一定是最短路径的)。
• 如果找到解，如何得到相应路径。深度优先遍历出栈中的路线即可。宽度优先需要借助其他方法记录相关信息。
• 搜索所有可能的解和最优解。深度优先在找到一个解之后可以回溯，找到所有解，直到遍历完整个状态找到所有的解。然后再选出最有解。宽度优先找到的第一个解就是最优解，当然也可以继续搜索，找到其他解。
• 搜索的时间开销。求解搜索问题的时间代价受限于状态空间的规模，实际求解的代价正比于找到解之前访问的状态个数。
• 搜索的空间开销。对于深度优先搜索，所需要的栈空间由找到一个解之前遇到过的最长的那一条搜索路径确定。对于宽度优先搜索，所需的队列空间由搜索过程中可能路径分支最多的那一层确定。

如果一个问题可使用空间搜索方法解决，那是用深度优先还是宽度优先，需要根据具体情况，也就是上面的性质来进行选择。

六、补充

1、与栈和队列相关的结构

双端队列

deque,它允许在两端插入和删除元素。
双端队列的实现方式

• 双链表可以支持在两端都是O(1)时间的插入和删除元素。
• 循环表。也可以支持O(1)时间的两端插入和删除。

python的deque类

python标准库中collections定义的deque类型，提供了一种双端队列的操作，它是采用双链表的技术实现的，但是其中每个链接结点里顺序存储一组元素。

2、问题讨论

问题：对于栈和队列，既然链表能实现统一的O(1)，那么为什么还要考虑顺序实现呢？

答：因为计算机的分级缓存结构(参考csapp第1章的存储管理)。如果连续进行一批内存访问是局部的，操作速度就会很快。因此，在考虑程序的效率时，一个重要线索就是对计算机内存使用的局部化。而链接结构的一个特点是，其中结点在内存中是任意分散的，因此，对链表元素的访问是在很多位置的内存单元跳来跳去的，因此它的效率没有顺序表实现的高。