DDT： deep descriptor transform 论文解析

论文参考链接：https://arxiv.org/abs/1705.02758

主要思想

提出了一种利用预训练模型(Imagenet Pretrained)来做解决目标共定位（object co-localization）问题。目标共定位即给定一个图像集，这个图像集中大部分图像区域都是某一个物体如飞机，则将所有飞机的区域定位出来（bounding box）。如下图所示为该论文的pipeline，整个过程是无监督的，即随便给定一个图像集，它主要包含某一类物体，算法可以将图像集中该类目标全部进行定位出来。

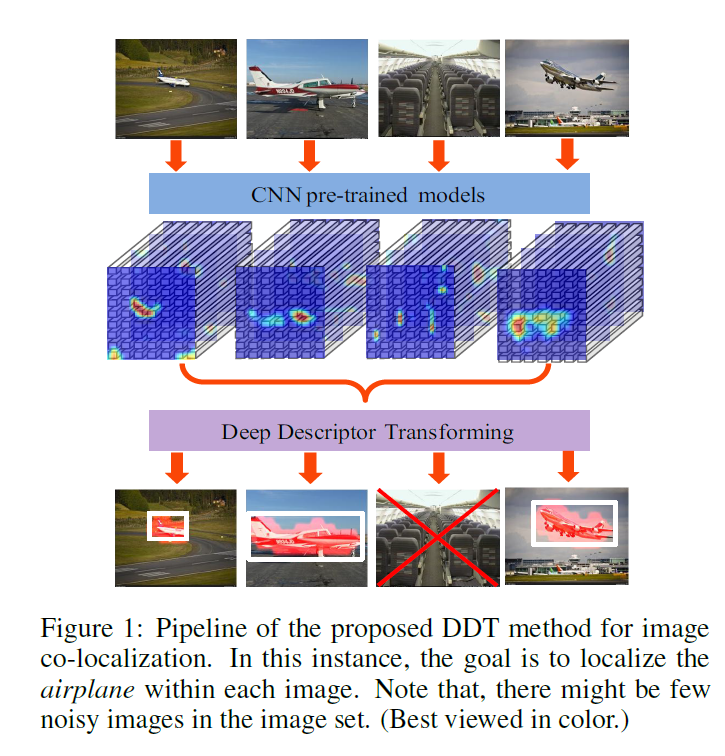
论文的主要贡献是提出了DDT模块，利用该模块可以实现无监督的目标共定位。

DDT模块

图像集{({ I_1, I_2, ... , I_n })}，经过CNN后得到该集合的特征向量(D_{set})，其shape: ((n, w, h, c))，这里我们假设图像集的所有图像大小相同，n代表图像集的图像数量，(w)，(h)分别代表特征图的宽和高，(c)代表特征图的通道维数。将(D_{set}) reshape 成 ((n*w*h, c))的张量并对其进行均值归0处理，得到(D_{reshpae})，表示具有(n*w*h)个长度为(n)的特征向量。

对(D_{reshape})进行PCA降维, 取最大特征值对应的特征向量作为基向量(xi_{1})，(xi_{1} in R^c)。
计算整个图像集在(xi_{1})上的投影：

[P_{set} = D_{reshape} * xi_{1} ]

将(P_{set}) reshape回单张图像得到{(P_1, P_2, ... , P_n)}，则(P_i)大于0的区域即为co-location，在进行后续的postprocessing就可以得到最终的bounding box了。

理解

PCA找出最大的特征值对应的特征向量，将图像的特征投影到该方向，如果值为正说明是正相关的，即图像集的共性被找到了，这个共性的区域就是co-location。PCA的理解可以参考这个博客，这里不再赘述。

实验结果

评价指标CorLoc

we take the correct localization (CorLoc) metric for evaluating the proposed method. CorLoc is defined as the percentage of images correctly localized according to the PASCAL-criterion.
即根据PASCAL的IOU标准（IOU>0.5）正确定位的图像数量占总共的图像数量的百分比。

数据集

作者在三个数据即上进行了实验以下给出三个数据集的基本信息：

1. Object Discovery dataset 连接：有三个类别,car, plane, horse; 每张图一个目标，有部分图是没有目标的； 每次处理的图像集大小为100.
2. PASCAL VOC (07，12)：使用trainval上的数据。对于大目标如飞机，基本上是一个目标一个图，背景简单；但是小目标如cup，背景复杂可能有多个不同类别目标同时出现一个图。
3. ImageNet Subsets：不包含Imagenet训练集中的类别，用此来说明模型的泛化能力。

实验结果

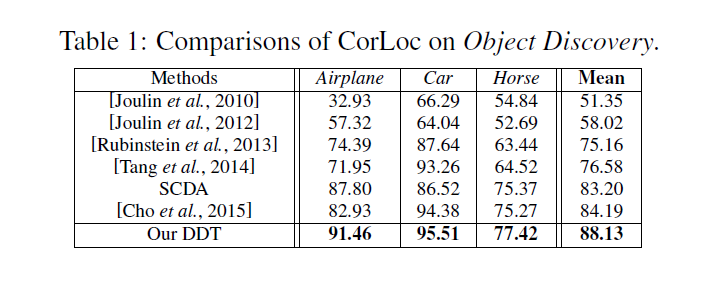
可以看到SCDA的方法结果也不错，因为该数据集是一个目标一张图，所以这种方法也取得了不错结果

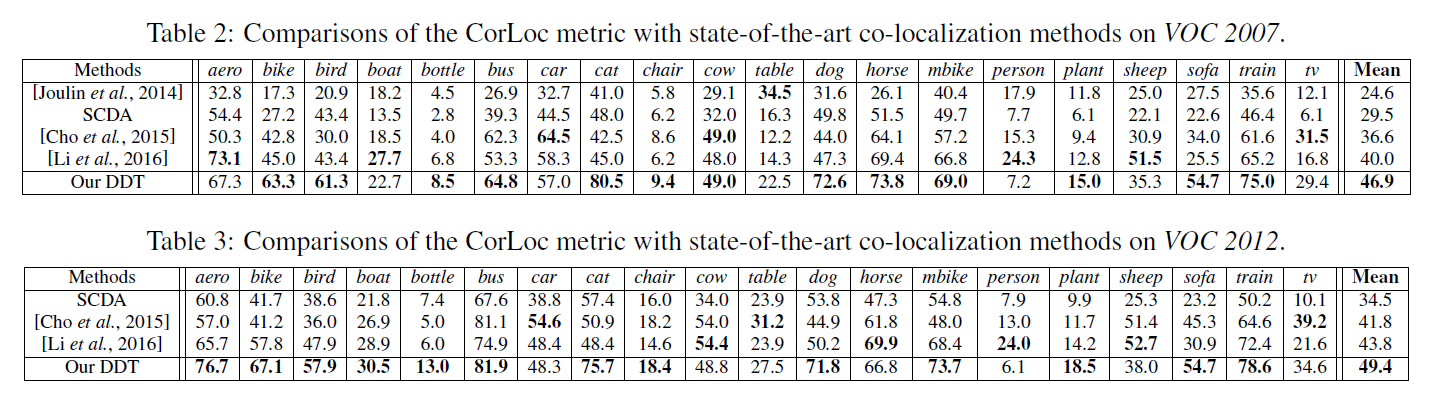
两个VOC数据集上的结果，可以看到大物体的结果较好，而小物体如cup的结果较差。

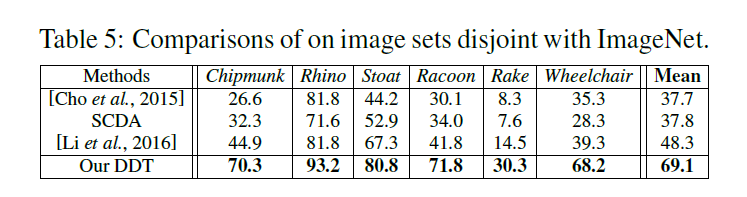
这是在ImaeNet Subsets上的结果，算法也取得了比较不错的结果。

这是与半监督学习算法的结果的对比，算法也获得了 competitive 的结果。

量化结果

---