java实现十大排序算法

参考：

https://www.cnblogs.com/onepixel/articles/7674659.html

这个博客写的很好，而且还有每个排序算法的动画，非常值得一看。

一、概览

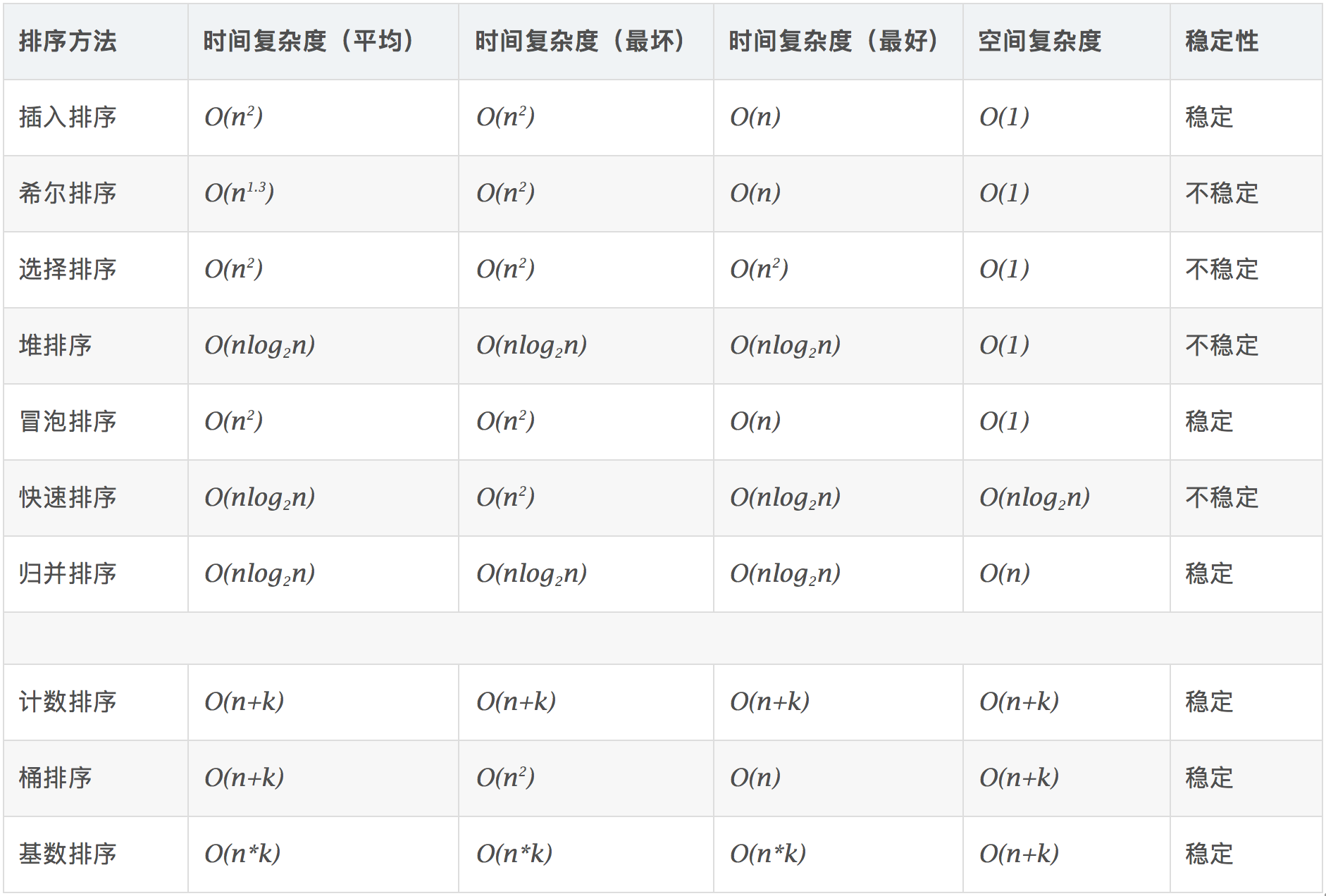
二、java实现

public class SortUtils {
    /**
     * 1.插入排序
     * 从第二个元素开始和前面的有序序列进行比较，
     * 如果小于有序元素的最后一个，则向前再向前，一直找到合适的位置插入
     * 然后插入位置的元素和它之后的元素统一向后移动一位
     * 插入排序理解起来不难，难点在于边界的确定
     */

    public static void insertSort(Integer[] arr) {
        //第一个数据肯定有序，所以从第二个数据开始跟有序序列做比较
        for (int i = 1; i < arr.length; i++) {
            Integer data = arr[i];
            int j = i - 1;
            //从后向前寻找arr[i]的插入位置
            while (data < arr[j] && j > 0) {
                j--;
            }
            //把j+1~i的所有数据统一向后移动一位，移动是逆序从后向前进行的
            for (int k = i; k > j; k--) {
                arr[k] = arr[k - 1];
            }
            arr[j + 1] = data;
        }
    }

    /**
     * 2.冒泡排序，最好理解
     * 一趟排序就可以把最大元素交换到队尾，然后下一次对前n-1个元素继续冒泡排序
     * @param arr
     */
    public static void bubbleSort(Integer[] arr) {
        int length = arr.length;
        for (int i = 0; i < length; i++) {
            for (int j = 0; j < length - i - 1; j++) {
                if (arr[j] > arr[j + 1]) {
                    exchange(arr, j, j + 1);
                }
            }
        }
    }

    /**
     * 3.选择排序
     * 始终选择未排序序列中的最小元素，插入到已排序序列的最后
     *
     * @param arr
     */
    public static void selectSort(Integer[] arr) {
        int length = arr.length;
        for (int j = 0; j < length; j++) {
            Integer minD = Integer.MAX_VALUE;
            int index = 0;
            for (int i = j; i < length; i++) {
                if (arr[i] < minD) {
                    minD = arr[i];
                    index = i;
                }
            }
            //循环结束，找到了最小元素和最小元素的下标
            Integer old = arr[j];
            arr[j] = minD;
            arr[index] = old;

        }
    }

    /**
     * 4.希尔排序
     * 可以认为是插入排序的改进版
     * 通过将原数组分解成不同步长的子序列，对子序列进行插入排序
     * 不断缩短步长，直到步长为一
     *
     * @param arr
     */
    public static void shellSort(Integer[] arr) {
        //初始步长为数组长度的一半
        int step = arr.length / 2;
        //while循环内部还是一个插入排序,与基本插入排序相比多了下标越界的校验
        while (step > 0) {
            for (int i = step; i < arr.length; i++) {
                Integer data = arr[i];
                int j = i - step;
                //从后向前寻找arr[i]的插入位置
                while (j >= 0 && data < arr[j]) {
                    j = j - step;
                }
                //把j+1~i的所有数据统一向后移动一位，移动是逆序从后向前进行的
                for (int k = i; k > j && k - step >= 0; k = k - step) {
                    arr[k] = arr[k - step];
                }
                arr[j + step] = data;
            }
            step = step / 2;
        }
    }

    /**
     * 5.归并排序
     * 对数组进行递归的拆分，直到每个数组只有一个元素，此时一定是有序的
     * 然后将这两个最小的有序数组进行合并再合并
     *
     * @param arr
     */
    public static void mergeSort(Integer[] arr, int start, int end) {
        if (start < end) {
            int q = (start + end) / 2;
            mergeSort(arr, start, q);
            mergeSort(arr, q + 1, end);
            merge(arr, start, q, end);
        }
    }

    private static void merge(Integer[] arr, int start, int q, int end) {
        //新建两个辅助数组,n1,n2是实际存放元素的长度
        int n1 = q - start + 1;
        int n2 = end - q;
        //每个数组多一个哨兵元素空间
        Integer[] left = new Integer[n1 + 1];
        Integer[] right = new Integer[n2 + 1];
        //将原数组的元素复制到辅助数组
        for (int i = 0; i < n1; i++) {
            left[i] = arr[start + i];
        }
        for (int j = 0; j < n2; j++) {
            right[j] = arr[q + 1 + j];
        }
        //哨兵元素
        left[n1] = Integer.MAX_VALUE;
        right[n2] = Integer.MAX_VALUE;
        int m = 0;
        int n = 0;
        for (int k = start; k <= end; k++) {
            if (left[m] < right[n]) {
                arr[k] = left[m];
                m++;
            } else {
                arr[k] = right[n];
                n++;
            }
        }
    }

    /**
     * 6.快速排序
     * 通过一趟排序将待排记录分隔成独立的两部分，
     * 其中一部分记录的关键字均比另一部分的关键字小，
     * 则可分别对这两部分记录继续进行排序，以达到整个序列有序。
     *
     * @param arr
     */

    public static void quickSort(Integer[] arr, int start, int end) {
        if (start < end) {
            int q = partition(arr, start, end);
            quickSort(arr, start, q - 1);
            quickSort(arr, q + 1, end);
        }
    }

    /**
     * 分区是快速排序的关键
     * 将一个数组根据基准分成小于基准值和大于基准值的两部分
     * 特点：需要两个游标
     *
     * @param arr
     * @param start
     * @param end
     * @return
     */
    private static int partition(Integer[] arr, int start, int end) {
        //默认以最后一个元素为基准
        Integer base = arr[end];
        //i代表较小值的最大索引,j代表未知元素最小索引
        int i = start - 1;
        for (int j = start; j < end; j++) {
            if (arr[j] <= base) {
                i++;
                exchange(arr, i, j);
            }
        }
        exchange(arr, i + 1, end);
        return i + 1;

    }

    public static void exchange(Integer[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    /**
     * 7.堆排序:需要借助堆数据结构
     *
     * @param arr
     */
    public static void heapSort(Integer[] arr) {
        MHeap<Integer> heap = new MHeap<>();
        for (Integer integer : arr) {
            heap.insert(integer);
        }
        for (int i = 0; i < arr.length; i++) {
            arr[i] = heap.pop();
        }
    }

    /**
     * 8.计数排序
     * 统计数组中小于一个元素所有元素的个数，这个个数正好就是它在新数组中的下标
     *
     * @param arr
     */
    public static Integer[] countSort(Integer[] arr) {
        Integer[] result = new Integer[arr.length];
        Integer[] c = new Integer[100];
        Arrays.fill(c, 0);
        for (int i = 0; i < arr.length; i++) {
            c[arr[i]] = c[arr[i]] + 1;
        }

        for (int i = 1; i < c.length; i++) {
            c[i] = c[i] + c[i - 1];
        }
        for (int i = 0; i < arr.length; i++) {
            Integer index = c[arr[i]];
            result[index - 1] = arr[i];
        }
        return result;
    }

    /**
     * 9.基数排序
     * 按照从低位到高位的顺序依次对数组进行排序
     * 基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。
     *
     * @param arr
     */
    public static void radixSort(Integer[] arr, int d) {
        //从个位到十位再到百位
        for (int i = 1; i <= d; i++) {
            doRadixSort(arr, i);
        }
    }

    /**
     * 借用临时数组存放每次基数排序的结果
     *
     * @param arr
     * @param degree
     */
    private static void doRadixSort(Integer[] arr, int degree) {
        //临时数组
        Integer[][] tempArray = new Integer[10][10];
        Integer[] indexArray = new Integer[10];
        Arrays.fill(indexArray, 0);
        for (Integer integer : arr) {
            int intByDegree = getIntByDegree(integer, degree);
            Integer idx = indexArray[intByDegree];
            tempArray[intByDegree][idx] = integer;
            indexArray[intByDegree] = indexArray[intByDegree] + 1;
        }

        int nd = 0;
        for (int i = 0; i < tempArray.length; i++) {
            Integer len = indexArray[i];
            for (int j = 0; j < len; j++) {
                arr[nd] = tempArray[i][j];
                nd++;
            }
        }

    }

    /**
     * 获取最大数的位
     *
     * @param maxVal
     * @return
     */
    private static int getDegree(Integer maxVal) {
        int i = 0;
        while (maxVal != 0) {
            i++;
            maxVal = maxVal / 10;
        }
        return i;
    }

    /**
     * 1-个位，2=10位
     * 获取当前位的值
     *
     * @param data
     * @param degree
     * @return
     */
    private static int getIntByDegree(Integer data, int degree) {
        return (int) ((data / Math.pow(10, degree - 1)) % 10);
    }

    /**
     * 10.桶排序
     * 桶是有序的，对桶内数据再排序，然后合并
     * 关键是如何进行分桶，使得每个桶的元素相差不大
     *
     * @param arr
     */
    public static void bucketSort(Integer[] arr) {
        int bucketNum = 0;
        //获取最大数的位数，即为桶数
        for (Integer integer : arr) {
            if (bucketNum < getDegree(integer)) {
                bucketNum = getDegree(integer);
            }
        }
        Integer[] indexArray = new Integer[bucketNum];
        Arrays.fill(indexArray, 0);
        //构造m*n的二维数组，m是桶数
        Integer[][] buckets = new Integer[bucketNum][arr.length];
        //遍历原数组，根据特征把数放入不同的桶
        for (Integer integer : arr) {
            //不同位的数放入不同桶
            int degree = getDegree(integer);
            int idx = degree - 1;
            //indexArray存放二级索引
            Integer index = indexArray[idx];
            buckets[idx][index] = integer;
            indexArray[idx] = indexArray[idx] + 1;
        }
        //对每个桶分别排序
        for (int i = 0; i < bucketNum; i++) {
            Integer[] bucket1 = buckets[i];
            Integer length = indexArray[i];
            quickSort(bucket1, 0, length - 1);
        }
        int newIndex = 0;
        //将桶的数据重新放回数组
        for (int i = 0; i < bucketNum; i++) {
            Integer len = indexArray[i];
            for (int j = 0; j < len; j++) {
                arr[newIndex] = buckets[i][j];
                newIndex++;
            }
        }
    }

    public static void main(String[] args) {
        Integer[] array = {76, 1, 43, 22, 5, 34, 547, 17, 18, 9};
//        insertSort(array);
//        bubbleSort(array);
//        selectSort(array);
//        heapSort(array);
//        quickSort(array,0,array.length-1);
//        mergeSort(array, 0, array.length - 1);
//        shellSort(array);
//        Integer[] array1 = countSort(array);
//        bucketSort(array);
        radixSort(array, 3);
        System.out.println(Arrays.toString(array));
    }
}