计算圆的包含（两两圆不相交）

问题

给出(n)个圆，求每个圆被哪个圆直接包含（两两圆不相交），如果(A)直接包含(B)，就是不存在(C)使得(A)包含(C)，(C)包含(B)。

算法1

lzhorz。

直接用K-D树，暴力解决此问题。

算法2

利用扫描线是一个很好的思路，下面我用的都是垂直的扫描线。

一开始我想把一个圆覆盖(Y)轴的部分堆加，当加入一个圆时判断它的圆心是被哪个最上面的部分覆盖。不过这样很容易画出反例：

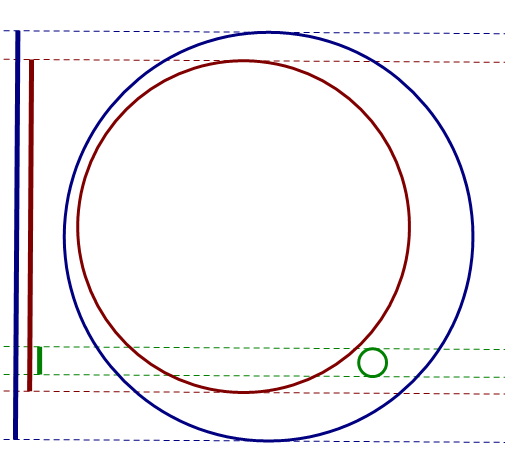
按照上面判断的方法，绿色的圆会被误判为被褐色的圆覆盖。

新的方法

lhorz。

把圆拆成两个部分，一个上弧，一个下弧。

判断一个新加入的圆(A)被哪个圆直接包含，可以找到离这个圆最近（但必须在这个圆的上面）一个弧，然后我们就得到了这个弧的“主人”圆(B)，如果这个弧是上弧，说明圆(B)包含圆(A)；如果是下弧，则说明直接包含圆(B)的圆(C) 直接包含了圆(A)。

代码非常好写，但是我调试了近半小时QAQ。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <set>
#include <assert.h>
#include <vector>
using namespace std;

typedef long long i64;

const int MAXN = (int) 1e5 + 3;
const double EPS = 1e-8;

template <class T>
T sqr(const T &x) {
	return x * x;
}

struct Circle {
	int x, y, r;

	void read() {
		scanf("%d%d%d", &x, &y, &r);
	}
};

int n;
Circle A[MAXN];
int fa[MAXN];

int globalX;

double calc(const pair<int, int> &a) {
	return (double) A[a.first].y +
		sqrt(sqr((i64) A[a.first].r) - sqr((i64) A[a.first].x - globalX)) *
		a.second;
}

struct cmp {
	bool operator () (const pair<int, int> &a, const pair<int, int> &b) {
		double tmp = calc(a) - calc(b);
		if (fabs(tmp) > EPS) return tmp < 0;
		return a < b;
	}
};

int main() {
	freopen("kendo.in", "r", stdin);
	freopen("kendo.out", "w", stdout);

	scanf("%d", &n);
	vector< pair<pair<int, int>, int> > key;
	for (int i = 0; i < n; i ++) {
		A[i].read();
		key.push_back(make_pair(make_pair(A[i].x - A[i].r, 1), i));
		key.push_back(make_pair(make_pair(A[i].x + A[i].r, -1), i));
	}
	sort(key.begin(), key.end());

	set< pair<int, int>, cmp> mySet;
	fill(fa, fa + n, -1);
	for (int i = 0, _i = key.size(); i < _i; i ++) {
		int j = key[i].second;
		globalX = key[i].first.first;
		if (key[i].first.second == 1) {
			set< pair<int, int> >::iterator tmp = mySet.lower_bound(make_pair(j, 1));
			if (tmp != mySet.end()) {
				if (tmp->second == -1) fa[j] = fa[tmp->first];
				else fa[j] = tmp->first;
			}
			mySet.insert(make_pair(j, 1));
			mySet.insert(make_pair(j, -1));
		}
		else {
			mySet.erase(make_pair(j, 1));
			mySet.erase(make_pair(j, -1));
		}
	}
	
	return 0;
}

注：答案存放在fa数组。