总结对比下(L_1) 损失函数,(L_2) 损失函数以及( ext{Smooth} L_1) 损失函数的优缺点。
均方误差MSE ((L_2) Loss)
均方误差(Mean Square Error,MSE)是模型预测值(f(x)) 与真实样本值(y) 之间差值平方的平均值,其公式如下
其中,(y_i)和(f(x_i))分别表示第(i)个样本的真实值及其对应的预测值,(n)为样本的个数。
忽略下标(i) ,设(n=1),以(f(x) - y)为横轴,MSE的值为纵轴,得到函数的图形如下:
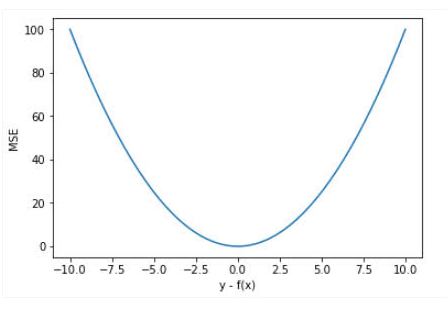
MSE的函数曲线光滑、连续,处处可导,便于使用梯度下降算法,是一种常用的损失函数。 而且,随着误差的减小,梯度也在减小,这有利于收敛,即使使用固定的学习速率,也能较快的收敛到最小值。
当(y)和(f(x))也就是真实值和预测值的差值大于1时,会放大误差;而当差值小于1时,则会缩小误差,这是平方运算决定的。MSE对于较大的误差((>1))给予较大的惩罚,较小的误差((<1))给予较小的惩罚。也就是说,对离群点比较敏感,受其影响较大。
如果样本中存在离群点,MSE会给离群点更高的权重,这就会牺牲其他正常点数据的预测效果,最终降低整体的模型性能。 如下图:
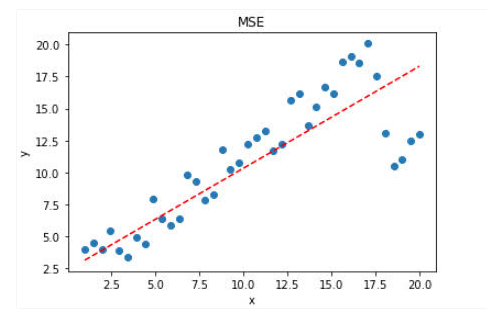
可见,使用 MSE 损失函数,受离群点的影响较大,虽然样本中只有 5 个离群点,但是拟合的直线还是比较偏向于离群点。
平均绝对误差((L_1) Loss)
平均绝对误差(Mean Absolute Error,MAE) 是指模型预测值(f(x))和真实值(y)之间距离的平均值,其公式如下:
忽略下标(i) ,设(n=1),以(f(x) - y)为横轴,MAE的值为纵轴,得到函数的图形如下:
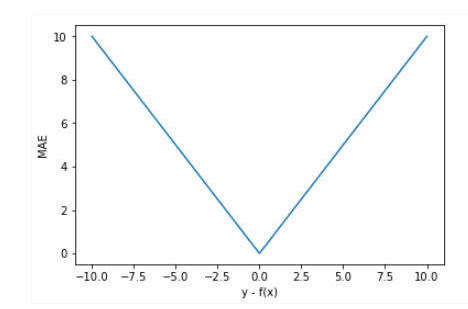
MAE曲线连续,但是在(y-f(x)=0)处不可导。而且 MAE 大部分情况下梯度都是相等的,这意味着即使对于小的损失值,其梯度也是大的。这不利于函数的收敛和模型的学习。但是,无论对于什么样的输入值,都有着稳定的梯度,不会导致梯度爆炸问题,具有较为稳健性的解。
相比于MSE,MAE有个优点就是,对于离群点不那么敏感。因为MAE计算的是误差(y-f(x))的绝对值,对于任意大小的差值,其惩罚都是固定的。
针对上面带有离群点的数据,MAE的效果要好于MSE。
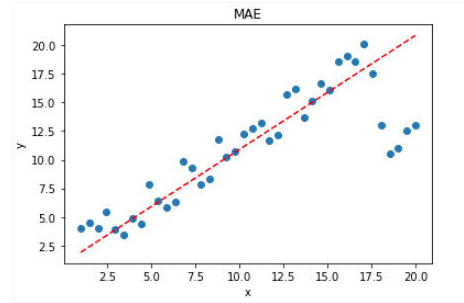
显然,使用 MAE 损失函数,受离群点的影响较小,拟合直线能够较好地表征正常数据的分布情况。
MSE和MAE的选择
-
从梯度的求解以及收敛上,MSE是由于MAE的。MSE处处可导,而且梯度值也是动态变化的,能够快速的收敛;而MAE在0点处不可导,且其梯度保持不变。对于很小的损失值其梯度也很大,在深度学习中,就需要使用变化的学习率,在损失值很小时降低学习率。
-
对离群(异常)值得处理上,MAE要明显好于MSE。
如果离群点(异常值)需要被检测出来,则可以选择MSE作为损失函数;如果离群点只是当做受损的数据处理,则可以选择MAE作为损失函数。
总之,MAE作为损失函数更稳定,并且对离群值不敏感,但是其导数不连续,求解效率低。另外,在深度学习中,收敛较慢。MSE导数求解速度高,但是其对离群值敏感,不过可以将离群值的导数设为0(导数值大于某个阈值)来避免这种情况。
在某些情况下,上述两种损失函数都不能满足需求。例如,若数据中90%的样本对应的目标值为150,剩下10%在0到30之间。那么使用MAE作为损失函数的模型可能会忽视10%的异常点,而对所有样本的预测值都为150。这是因为模型会按中位数来预测。而使用MSE的模型则会给出很多介于0到30的预测值,因为模型会向异常点偏移。
这种情况下,MSE和MAE都是不可取的,简单的办法是对目标变量进行变换,或者使用别的损失函数,例如:Huber,Log-Cosh以及分位数损失等。
Smooth (L_1) Loss
在Faster R-CNN以及SSD中对边框的回归使用的损失函数都是Smooth (L_1) 作为损失函数,
其中,(x = f(x_i) - y_i) 为真实值和预测值的差值。
Smooth (L_1) 能从两个方面限制梯度:
- 当预测框与 ground truth 差别过大时,梯度值不至于过大;
- 当预测框与 ground truth 差别很小时,梯度值足够小。
对比(L_1) Loss 和 (L_2) Loss
其中(x)为预测框与groud truth之间的差异:
上面损失函数对(x)的导数为:
上面导数可以看出:
-
根据公式-4,当(x)增大时,(L_2)的损失也增大。 这就导致在训练初期,预测值与 groud truth 差异过于大时,损失函数对预测值的梯度十分大,训练不稳定。
-
根据公式-5,(L_1)对(x)的导数为常数,在训练的后期,预测值与ground truth差异很小时,(L_1)的导数的绝对值仍然为1,而 learning rate 如果不变,损失函数将在稳定值附近波动,难以继续收敛以达到更高精度。
-
根据公式-6,( ext{Smotth } L_1)在(x)较小时,对(x)的梯度也会变小。 而当(x)较大时,对(x)的梯度的上限为1,也不会太大以至于破坏网络参数。(Smooth L_1)完美的避开了(L_1)和(L_2)作为损失函数的缺陷。
(L_1) Loss ,(L_2) Loss以及(Smooth L_1) 放在一起的函数曲线对比
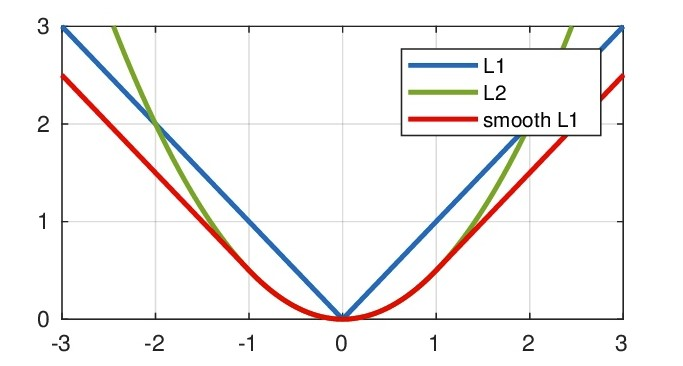
从上面可以看出,该函数实际上就是一个分段函数,在[-1,1]之间实际上就是L2损失,这样解决了L1的不光滑问题,在[-1,1]区间外,实际上就是L1损失,这样就解决了离群点梯度爆炸的问题
实现 (PyTorch)
def _smooth_l1_loss(input, target, reduction='none'):
# type: (Tensor, Tensor) -> Tensor
t = torch.abs(input - target)
ret = torch.where(t < 1, 0.5 * t ** 2, t - 0.5)
if reduction != 'none':
ret = torch.mean(ret) if reduction == 'mean' else torch.sum(ret)
return ret
也可以添加个参数beta 这样就可以控制,什么范围的误差使用MSE,什么范围内的误差使用MAE了。
def smooth_l1_loss(input, target, beta=1. / 9, reduction = 'none'):
"""
very similar to the smooth_l1_loss from pytorch, but with
the extra beta parameter
"""
n = torch.abs(input - target)
cond = n < beta
ret = torch.where(cond, 0.5 * n ** 2 / beta, n - 0.5 * beta)
if reduction != 'none':
ret = torch.mean(ret) if reduction == 'mean' else torch.sum(ret)
return ret
总结
对于大多数CNN网络,我们一般是使用L2-loss而不是L1-loss,因为L2-loss的收敛速度要比L1-loss要快得多。
对于边框预测回归问题,通常也可以选择平方损失函数(L2损失),但L2范数的缺点是当存在离群点(outliers)的时候,这些点会占loss的主要组成部分。比如说真实值为1,预测10次,有一次预测值为1000,其余次的预测值为1左右,显然loss值主要由1000决定。所以FastRCNN采用稍微缓和一点绝对损失函数(smooth L1损失),它是随着误差线性增长,而不是平方增长。
Smooth L1 和 L1 Loss 函数的区别在于,L1 Loss 在0点处导数不唯一,可能影响收敛。Smooth L1的解决办法是在 0 点附近使用平方函数使得它更加平滑。
Smooth L1的优点
- 相比于L1损失函数,可以收敛得更快。
- 相比于L2损失函数,对离群点、异常值不敏感,梯度变化相对更小,训练时不容易跑飞。