三角函数解题中周期的选择技巧

前言

三角函数是高中阶段比较常见的周期函数，研究其性质或者解有关三角函数不等式时，肯定少不了周期性的考量。一般情况下基本周期我们都选([0，2pi])来研究，但不是所有问题都这样选取周期就简单，以下举例说明。

研究单调

例1 研究函数(y=2sin(3x+cfrac{pi}{4})+1)的单调区间。(整体思想：(X=3x+cfrac{pi}{4}))

分析：由于函数(y=2sin(3x+cfrac{pi}{4}[X])+1)的单调区间和函数(y=sinX)的单调区间相同，原因是函数(y=sinx)在纵轴方向上平移和伸缩时并不影响原函数的单调区间

故只需要研究(y=sinX)的单调性，就可以仿照完成问题的求解。

函数(y=sinX)在区间([2kpi-cfrac{pi}{2}，2kpi-cfrac{pi}{2}](kin Z))上单调递增，

在区间([2kpi+cfrac{pi}{2}，2kpi+cfrac{3pi}{2}](kin Z))上单调递减，

故令(3x+cfrac{pi}{4}in [2kpi-cfrac{pi}{2}，2kpi+cfrac{pi}{2}](kin Z))，

即得到原函数的单调递增区间；

令(3x+cfrac{pi}{4}in [2kpi+cfrac{pi}{2}，2kpi+cfrac{3pi}{2}](kin Z))，

即得到原函数的单调递减区间；

小结：本类问题中，基本周期的选择是([-cfrac{pi}{2}，cfrac{3pi}{2}])，原因是这样选用的周期，得到的单调区间是连续的。如果选取基本周期为([0，2pi])，后续的表达由于不连续，反倒很不方便。

解不等式

例2 解不等式(2sin(x+cfrac{pi}{4})-1>0)。

分析：先转化为(sin(x+cfrac{pi}{4})>cfrac{1}{2})，此时基本周期选([0，2pi])，

可以看到，当(sinx>cfrac{1}{2})时，在基本周期内的解集为((cfrac{pi}{6}，cfrac{5pi}{6}))，

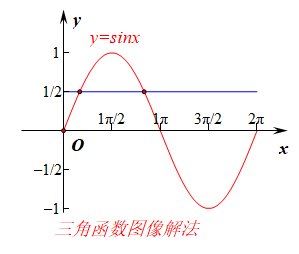
故先令(x+cfrac{pi}{4}in (cfrac{pi}{6}，cfrac{5pi}{6}))，解得(xin (-cfrac{pi}{12}，cfrac{7pi}{12}))

故在(R)上的原不等式的解集为(xin (2kpi-cfrac{pi}{12}，2kpi+cfrac{7pi}{12})(kin Z))。

例-变式 解不等式(2sin(x+cfrac{pi}{4})-1<0)。

这时候我们如果选基本周期为([0，2pi])，就很不方便，

原因是(sinx<cfrac{1}{2})的解集为([0，cfrac{pi}{6}))和((cfrac{5pi}{6}，2pi))是不连续的，表达很不方便，

那么怎么样作能更好些呢？

此时我们可以选基本周期为([cfrac{pi}{6}，cfrac{13pi}{6}])，就很方便[当然也可选基本周期为([cfrac{pi}{2}，cfrac{5pi}{2}])，不再赘述]；

则先得到(sin(x+cfrac{pi}{4})<cfrac{1}{2})在基本周期内的解为(x+cfrac{pi}{4}in (cfrac{5pi}{6}，cfrac{13pi}{6}))，

从而解得在基本周期内的解(x in (cfrac{7pi}{12}，cfrac{23pi}{12}))，

然后拓展[就是给不等式的两边同时添加(2kpi(kin Z))]，得到(R)上的原不等式的

解集为(xin (2kpi+cfrac{7pi}{12}，2kpi+cfrac{23pi}{12})(kin Z))。