前言
一、计数策略
-
注意三个维度;
-
利用类比思维;
-
注意剔除重复情形;
二、典例剖析
分析:先做出正方体,以及六个面的中心,如下图所示,
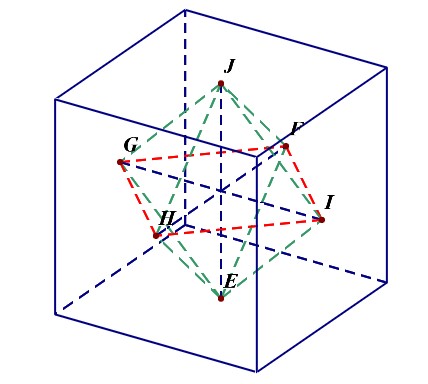
然后将这六个中心两两相连,得到线段为(C_6^2=15)条,如下图所示,外观是个正八面体。
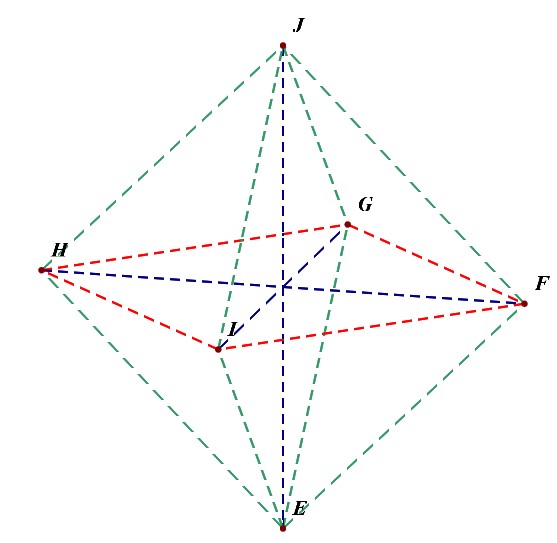
接下来,我们先考虑(l_1perp l_2)的所有情形,为便于计数,我们对线段依次编号①②③④⑤⑥⑦⑧⑨⑩⑪⑫⑬⑭⑮;
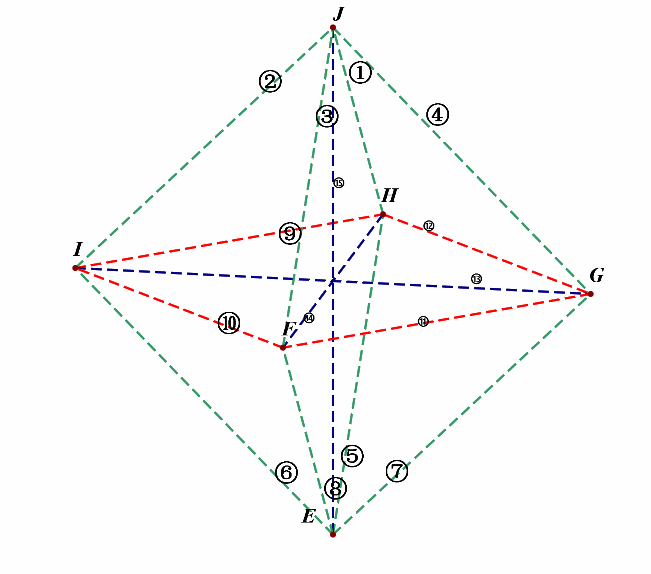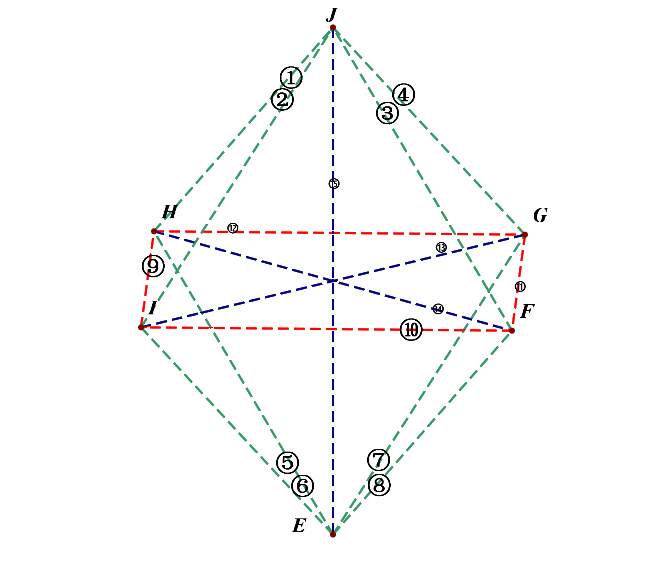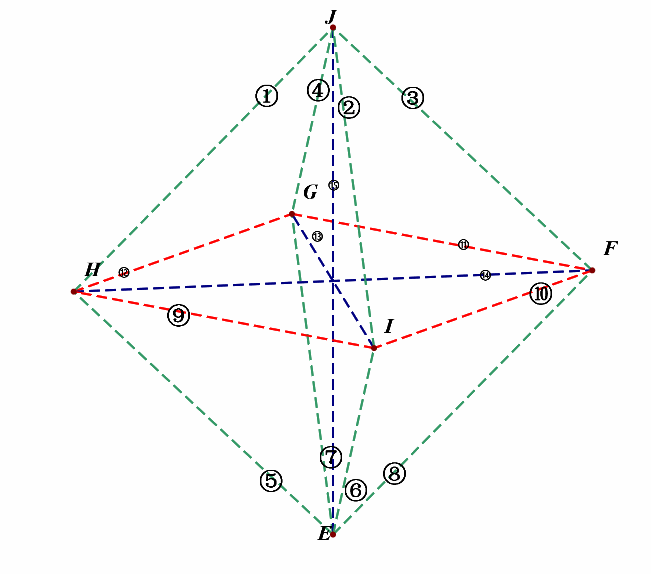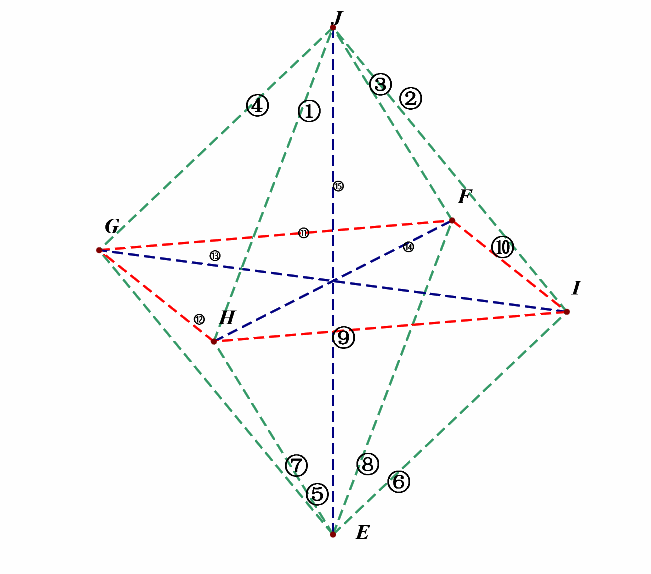
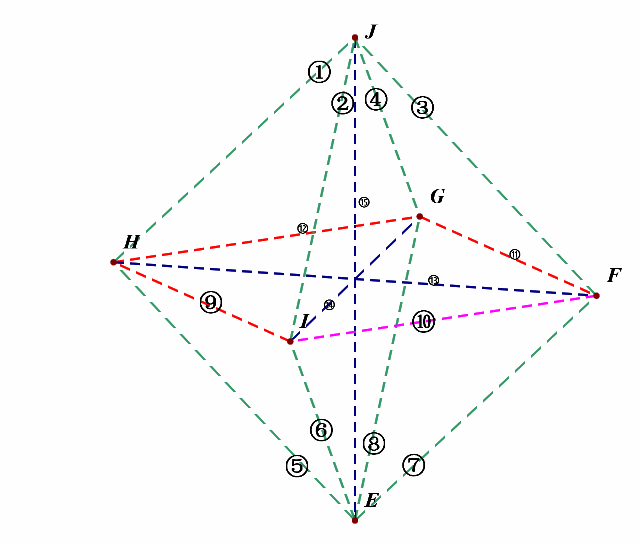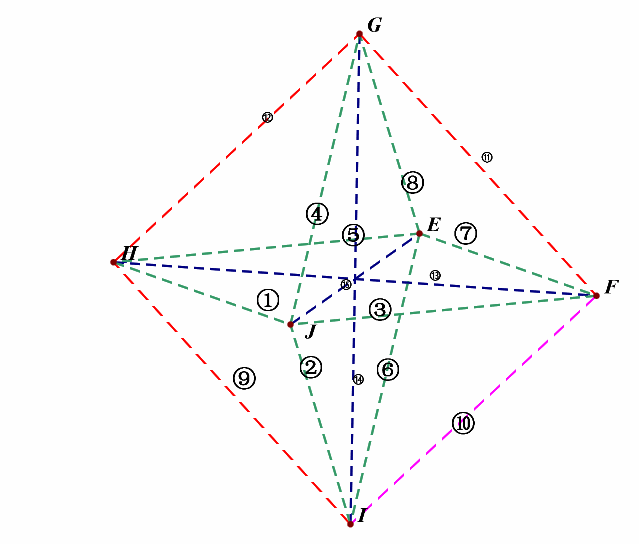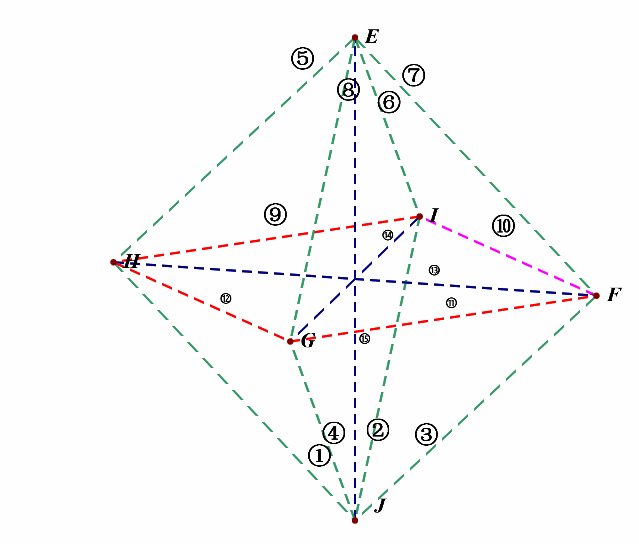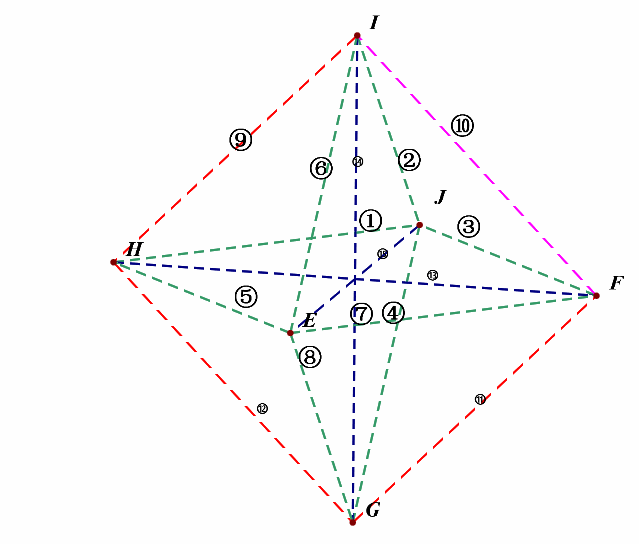
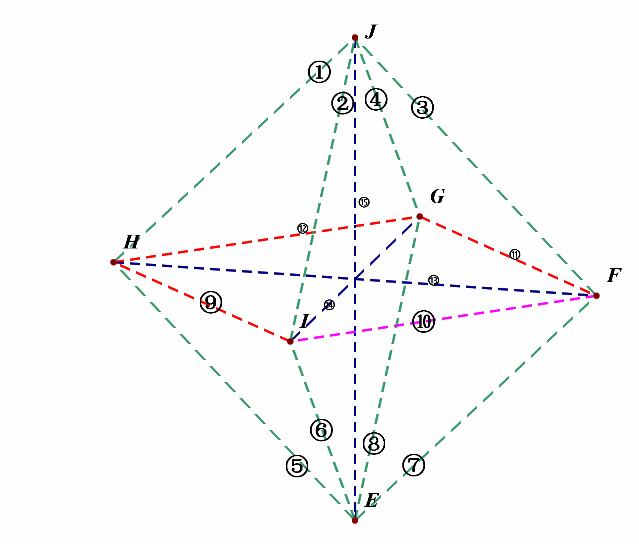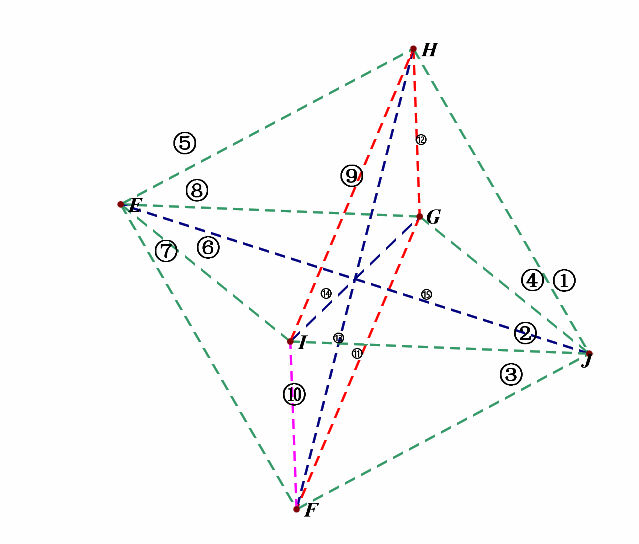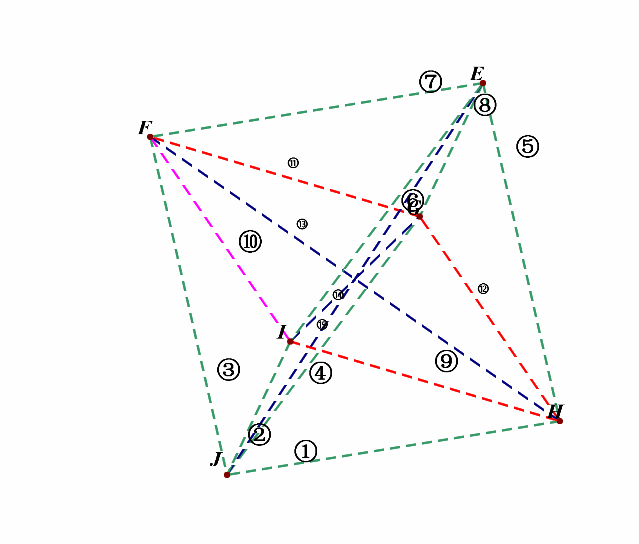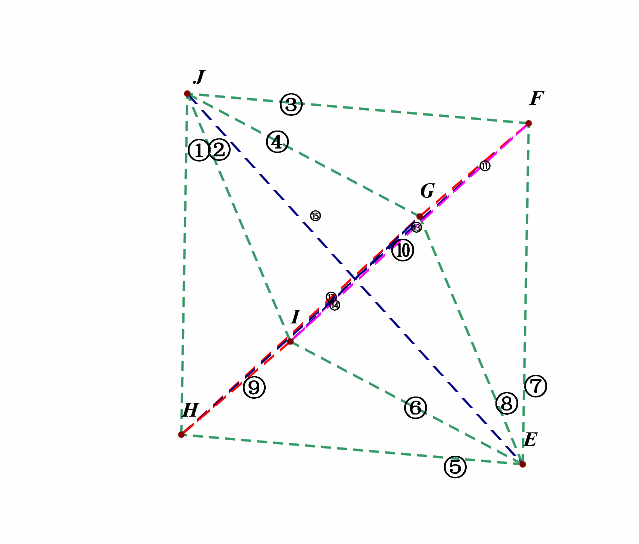
(1^{circ}),绕(z)轴方向,即上下方向的维度上,相互垂直的直线有:
和⑮垂直的直线有:⑨,⑩,⑪,⑫,⑬,⑭,共有6对;
以及在(yoz)平面中,相互垂直的直线有①③;③⑤;⑤⑦;①⑦,共有4对;
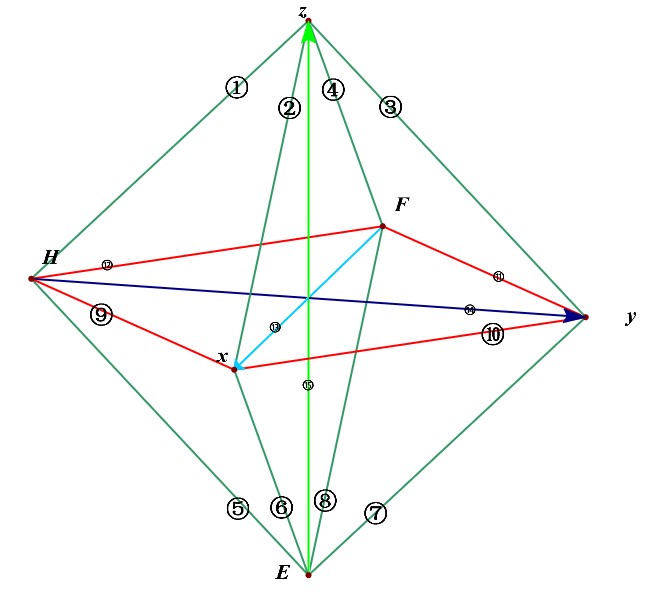
(2^{circ}),绕(x)轴方向,即前后方向的维度上,相互垂直的直线有:
和⑬垂直的直线有:①,③,⑤,⑦,⑭,共有5对;
以及在(xoz)平面中,相互垂直的直线有②④;④⑧;⑥⑧;②⑥;共有4对;

(3^{circ}),绕(y)轴方向,即左右方向的维度上,相互垂直的直线有:
和⑭垂直的直线有:②,④,⑥,⑧,共有4对;
以及在(xoy)平面中,相互垂直的直线有⑨⑩;⑩⑪;⑪⑫;⑨⑫;共有4对;
故所有情形有(6+5+4+3 imes 4=27),其中属于异面垂直的直线有:每个维度上有4对,三个维度,共有12对,
故所求概率为(P=cfrac{12}{27}=cfrac{4}{9})。
分析:我们容易判断该问题是古典概型,分母是(C_8^4),难点是分子的确定。如图所示,我们选其中一个顶点,比如选(A),
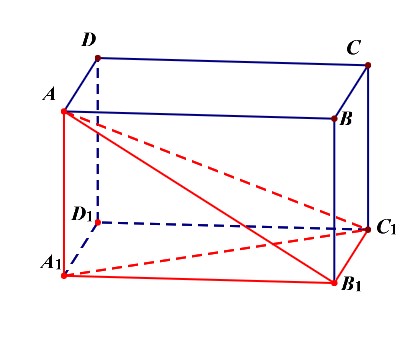
则过点(A)有三个维度,上下,左右,前后,先选定一个维度,比如上下,由于点(A)在上底面,故我们在下底面中寻找,自然先找到点(A'),再找到点(B'),最后找到点(C'),这样一个“三节棍体”的四面体就得到了,我们先判断一下为什么四面体(A-A_1B_1C_1)称为“三节棍体”的四面体,然后回头思考其中的三节棍是哪些线段?(AA_1),(A_1B_1),(B_1C_1),这三条线段的特点为两两垂直。
当选了点(A)后,在下底面就不会选(B_1)、(C_1)、(D_1)三个点,而会接着选(A1)、(D_1)、(C_1)三个点,得到“三节棍体”的四面体(A-A_1D_1C_1),于是在一个维度上有2个符合题意的“三节棍体”,那么在三个维度上共有(3 imes2=6)个“三节棍体”;同理,类似点(A)的顶点共有8个,故共有“三节棍体”的个数为(6 imes 8=48)个;
接下来考虑是否有重复的情形,其实上述的情形刚好重复了一倍,比如当顶点为(C_1)时,得到的“三节棍体”(C_1-A_1D_1A)和(A-A_1D_1C_1)是相同的,这样应该有(cfrac{1}{2} imes 48=24),
故所求概率为(P=cfrac{24}{C_8^4}=cfrac{12}{35})。