因式分解法

前言

高中阶段使用到因式分解的数学内容有解不等式(尤其是解含参不等式)、导数、解三角形或判断三角形形状等；

• 因式分解的主要方法有：提取公因式法；公式法；拆添项法；十字相乘法；分组分解法；多项式除法；待定系数法；

常用方法

• 提取公因式法；

引例，已知(f(x)=(x-2)e^x+a(x-1)^2)．求(f'(x))；

分析：(f'(x)=1cdot e^x+(x-2)cdot e^x+2a(x-1))(=e^x(x-1)+2a(x-1))(=(x-1)(e^x+2a))，

引例，涉及提取公因式法的常用变形

$4^n=(2^2)^n=(2^n)^2;$

$2^n+2^n=2^{n+1};$

$2^{n+1}-2^n=2^n;$

$2^{n}-2^{n-1}=2^{n-1}$；

$2^{n+1}+2^n=3cdot 2^n$；

$2^{-(n+1)}cdot 2=2^{-n}$；

$2^ncdot 2^n=2^{2n}$；

$3^{n-1}-3^n=-2cdot 3^{n-1}$；

$2^{n+1}÷2^n=2;$

$frac{1}{2^n}+frac{1}{2^{n+1}}=frac{3}{2^{n+1}}$；

$3^{n-1}cdot 3^n=3^{2n-1}$；

$2^{n+1}cdot 2^n=2^{2n+1};$

• 拆添项法；

已知(3t^3-7t^2+4=0)，求(t)的值；

分析：先将方程拆项变形为(3t^3-3t^2-4t^2+4=0)，然后分组分解得到，(3t^2(t-1)-4(t-1)(t+1)) (=(t-1)(3t^2-4t-4)) (=(t-1)(t-2)(3t+2)=0)，

• 公式法；

(a^3pm b^3=(apm b)(a^2mp ab+b^2))；(a^2pm 2ab+b^2=(apm b)^2)；

• 十字相乘法，使用最为广泛。实际高三数学教学和考试中的解不等式常常是这样的，熟练掌握对你的数学学习会有帮助的。

①(x^2-5sqrt{2}x+8ge 0)，即((x-sqrt{2})(x-4sqrt{2})ge 0)；

②(x^2-(2m+1)x+m^2+m-2leq 0)，即([x-(m+2)][x-(m-1)]leq 0)；

③(x^2-3mx+(m-1)(2m+1)ge 0)；即([x-(m-1)][x-(2m+1)]ge 0)；

④(x^2-(a+a^2)x+a^3leq 0)，即((x-a)(x-a^2)leq 0)；

⑤(x^2-(a+1)x+aleq 0)，即((x-1)(x-a)leq 0)；

⑥(x^2-(2a+1)x+a(a+1)leq 0)；即((x-1)[x-(a+1)]leq 0)；

⑦(cfrac{x-2a}{x-(a^2+1)}<0(a eq 1))；即((x-2a)[x-(a^2+1)]<0)，解集为((2a，a^2+1))；

⑧(x^2+(m+4)x+m+3<0)，即((x+1)[x+(m+3)]<0)；

⑨(x^2-(a+cfrac{1}{a})x+1<0)，即((x-a)(x-cfrac{1}{a})<0)；

⑩(f'(x)=x+(a-e)-cfrac{ae}{x}=cfrac{x^2+(a-e)x-ae}{x}=cfrac{(x+a)(x-e)}{x})；

(2e^{2x}-e^xa-a^2=(e^x-a)cdot (2e^x+a))，

(g(x)=[f(x)]^2-2mcdot f(x)+m^2-1=0)，即([f(x)-(m-1)][f(x)-(m+1)]=0)

⑾(x^2-2ax+a^2-4=x^2-2ax+(a+2)(a-2)=[x-(a-2)][x-(a+2)]leq0)，即(a-2leq xleq a+2) ；

(a^2x^2+ax-2=0)，即((ax+2)(ax-1)=0)；

• 分组分解法，也能使用于高次式的分解，难点是不容易发现分组的思路。

比如(3x^3-7x^2+4=0)，可以分解为(3x^3-3x^3-4x^3+4=3x^2(x-1)-4(x^2-1)=(x-1)(3x^2-4x-4)=(x-1)(x-2)(3x+2))；

那么，上式的分解中怎么会想到将(-7x^2)分解为(-3x^2-4x^2)的呢？

• 试商法，原理：若(f(x)=0)，则(f(x))中至少含有一个因子(x)，即(f(x)=xcdot g(x))或(f(x)=xcdot a)((a)为常数)

对于上式(3x^3-7x^2+4=0)，先尝试令(x=0)，不满足方程，说明三次三项式(3x^3-7x^2+4)中不能分解出因式(x)；

再尝试令(x=1)，发现方程成立，说明三次三项式(3x^3-7x^2+4)中应该能分解出因式(x-1)，这样另外一个因式的最高次必然会降低为(2)次；

如果还不行再尝试(x=-1)，依次类推，(x=0)，(x=pm 1)，(x=pm 2)，等等如此；

那么用试商法得到其中一个因式后，如何得到剩余的因式呢，这可以用多项式除法来解释说明。

• 多项式除法，多用于三次式或高次式的分解

引例解方程，(x_0^3-3x_0^2+4=0)；

分析：先用试商法，令(x_0=0)，如果上述方程成立，说明方程能分解出因子(x_0)，本题目中显然不成立；

再令(x_0=1),上述方程不成立，说明方程不能分解出因子(x_0-1)；再令(x_0=-1),上述方程成立，

说明方程能分解出因子(x_0+1)；这样(x_0^3-3x_0^2+4=(x_0+1)(x_0^2+bx_0+c)(b，c是常数，待定))，这样做的目的是为了降次；

以下用多项式除法探求另一个因式，多项式除法如下图所示；

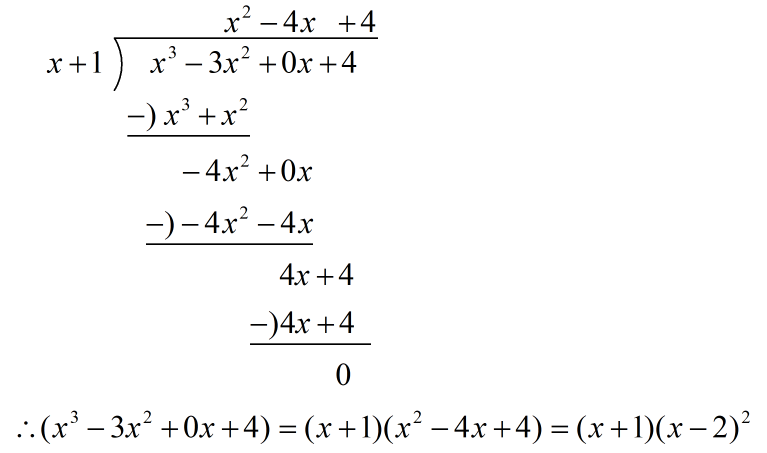
看完这个除法，你可能会有这样的想法：其一，多项式的除法和数字的除法本质做法是一样的；其二，这个做法还是比较麻烦；

能不能改进一下呢，回答是肯定的。

• 组合使用法

我们可以用试商法先确定一个因式，从而能确定分组分解的方向，即试商法和分组分解法组合使用。 接上例说明，由于我们知道必定有一个因式为((x_0+1))，故和(x_0^3)分组的只能是(1)，从而想到将(4)拆分为(1+3)，然后将(-3x_0^2)和(3)分组，如下所示：

如(x_0^3-3x_0^2+4=(x_0^3+1)-3x_0^2+3=(x_0^3+1)-3(x_0^2-1)) (=(x_0+1)(x_0^2-x_0+1)-3(x_0+1)(x_0-1)) (=(x_0+1)(x_0^2-x_0+1-3x_0+3)=(x_0+1)(x_0-2)^2)；

典例剖析

例1【2019届高三理科数学第三轮模拟训练题】【难点题目，综合程度高，对学生的运算能力要求很高】

已知正项等比数列({a_n})的前(n)项和为(S_n)，若(7S_6=3S_9)，(a_4=2)，则数列({a_{3n-2}+log_2a_n})的前(10)项的和(T_{10})=____________。

分析：先由条件容易判定，$q eq 1 $，由(7S_6=3S_9)，得到(7 imes cfrac{a_1(1-q^6)}{1-q}=3 imes cfrac{a_1(1-q^9)}{1-q})

转化得到(3q^9-7q^6+4=0)，令(q^3=t)，变形为(3t^3-7t^2+4=0)，

即(3t^3-3t^2-4t^2+4=0)，即(3t^2(t-1)-4(t-1)(t+1)=)((t-1)(3t^2-4t-4))(=(t-1)(t-2)(3t+2)=0)，

解得(t=1)(舍去)，(t=-cfrac{2}{3})(舍去)，(t=2)；

即(t=q^3=2)，则(a_n=a_4cdot q^{n-4}=2q^{n-4})，

则(a_{3n-2}=2cdot q^{3n-6}=2cdot (q^3)^{n-2}=2cdot 2^{n-2}=2^{n-1})；

(log_2a_n=log_22cdot q^{n-4}=1+(n-4)log_2q=1+(n-4)cdot cfrac{1}{3}log_2q^3)

(=1+(n-4)cdot cfrac{1}{3}log_22=1+cfrac{n-4}{3})；

则(T_{10}=(2^0+2^1+cdots+2^9)+[(1+cfrac{-3}{3})+(1+cfrac{-2}{3})+cdots+(1+cfrac{6}{3}))

(=cfrac{1(2^{10}-1)}{2-1}+10+cfrac{1}{3} imescfrac{(-3+6)10}{2}=1023+15=1038);

解后反思：巧妙利用指数幂的运算性质，可以大大简化本题目的运算过程，降低运算难度。

• 上次编辑时间：2019-07-20