争鸣|深层次理解几何概型的概念和求解

前言

一家之言，难免有挂一漏万之嫌，欢迎各位批评雅正，谢谢合作。

案例剖析

案例已知圆(M：x^2+y^2=4)，在圆(M)上随机取两个点(A)、(B)，使(|AB|leqslant 2sqrt{3})的概率是【(quad)】

$A.cfrac{1}{2}$ $B.cfrac{1}{3}$ $C.cfrac{2}{3}$ $D.cfrac{1}{5}$

【法1】[我的理解]：如图所示，在圆(M)上分别任意取两个点(A、B)，占满了圆上的任意两点，

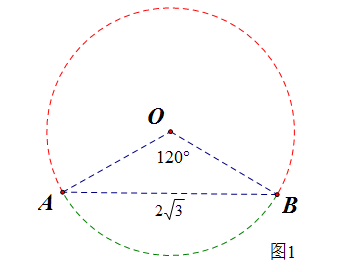
则所有情形应有无穷多种，且是等可能的，因此所有的样本空间应该用圆的周长(2picdot R=4pi)来度量，

令“(|AB| leq 2sqrt{3})”为事件(N)，则事件(N)的所有结果应该是：任取的两个点(A、B)应该都落在劣弧(overset{frown}{AB})上，

事件(N)的所有结果应该用劣弧(overset{frown}{AB})的弧长来度量，由于劣弧(overset{frown}{AB})对应的圆心角为(120^{circ}=cfrac{2pi}{3})，则弧长为(cfrac{4pi}{3})，

所以按照长度型几何概型得，所求的概率为(P(N)=cfrac{frac{4pi}{3}}{4pi}=cfrac{1}{3})。故选(B)

[思考1]：也可以按照角度型几何概型得到(P=cfrac{120^{circ}}{360^{circ}}=cfrac{1}{3})。

[思考2]：之所以可以用角度型也可以用长度型来理解和计算，是因为半径(OA)绕着点(O)旋转时的每一个角度都唯一对应圆周上的一个点，是一一对应的。

【法2】[化曲为直]：把圆剪开，就是一条长度为(4pi)的线段，任取点(A、B)相当于用圆规的两个脚落在线段上，那么所有的样本空间数有无穷多个，所有结果用线段的长度来度量，应该为(4pi)；原来在圆上任取的两个点使(|AB|leqslant 2sqrt{3})相当于在直线段上任取的两个点必须满足(|AB|leqslant cfrac{4pi}{3})，所有结果应该用(cfrac{4pi}{3})的长度来度量，

所以按照长度型几何概型得，所求的概率为(P(N)=cfrac{frac{4pi}{3}}{4pi}=cfrac{1}{3})。故选(B)

【法3】[有的资料给出的解法]：如图2所示，用先确定点(A)后确定点(B)的思路可知，

满足(|AB|leqslant 2sqrt{3})的情形有劣弧 (overset{frown}{AB})和劣弧 (overset{frown}{AB'})，

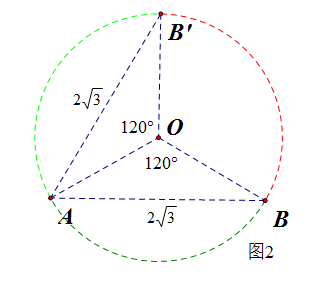
所以满足的情形应该是优弧(overset{frown}{BB'})，所以(P=cfrac{240^{circ}}{360^{circ}}=cfrac{2}{3})。

这种解法的算理是有错误的，当点(A、B)在优弧(overset{frown}{BB'})上任意取点时，是不满足条件(|AB| leq 2sqrt{3})的。

解后反思：点(A)，(B)位置确定是没有关联的，

【法4】[有的资料给出的解法]：如图3所示，满足(|AB| leq 2sqrt{3})的情形有劣弧 (overset{frown}{AB})和劣弧(overset{frown}{A'B'})，

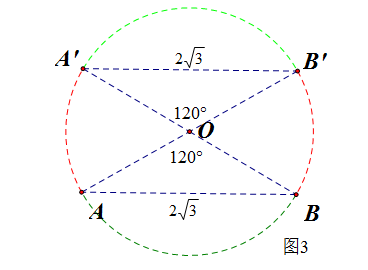
所以满足的情形应该是两段之和，所以(P=cfrac{240^{circ}}{360^{circ}}=cfrac{2}{3})。

这种解法也是有错误的，当点(A、B)分别在两个劣弧上任意取点时，是不满足条件(|AB| leq 2sqrt{3})的。

解后反思：这种错误的起源和我们写函数(y=cfrac{1}{x})的单调区间的错误是一样的。如我们写成单调减区间为((-infty，0)cup (0，+infty))，那么我们用定义验证时，当自变量(x_1， x_2)同时取在区间((-infty，0))或区间((0，+infty))时，都满足单调递减的定义，但是若(x_1in (-infty，0))且$x_2in(0，+infty) $时，验证是错误的。