前言
二者关系
- 函数的单调性与其导函数的正负间的关系:
设函数(y=f(x))在区间((a, b))内可导,[导数(Rightarrow)单调性]
若(f'(x)>0),函数(y=f(x))在区间((a, b))上单调递增;
若(f'(x)<0),函数(y=f(x))在区间((a, b))上单调递减;
设函数(y=f(x))在区间((a, b))内可导,[单调性(Rightarrow)导数]
若函数(y=f(x))在区间((a, b))上单调递增,则(f'(x)geqslant 0)且在其任一子区间内恒有(f'(x) eq 0);
若函数(y=f(x))在区间((a, b))上单调递减,则(f'(x)leqslant 0)且在其任一子区间内恒有(f'(x) eq 0);
提示:不一定成立。比如(y=x^{3})在(R)上为增函数,但其在(x=0)处的导数等于零。也就是说(f^{prime}(x)>0)是(y=f(x))在某个区间上递增的充分不必要条件,(f^{prime}(x)geqslant 0)是(y=f(x))在某个区间上递增的必要不充分条件。
-
一般地,如果一个函数在某一范围内的导数的绝对值较大,说明函数在这个范围内变化得快,这时,函数的图象就比较“陡峭”;反之,函数的图象就比较“平缓”。
-
利用导数求函数单调区间的基本步骤
(1).确定函数(f(x))的定义域;
(2).求导函数(f^{prime}(x));
(3).由(f'(x)>0)或(f^{prime}(x)<0),解出相应的(x)的取值范围。
当(f'(x)>0)时,(f(x))在相应的区间上是增函数;此时不能用(f'(x)geqslant 0)来求解,原因是(f'(x)>0)是(f(x))单调递增的充分不必要条件,而(f'(x)geqslant 0)是(f(x))单调递增的必要不充分条件;此时我们需要寻求的是充分条件。
当 (f'(x)<0)时,(f(x))在相应区间上是减函数。
法1:导数法,由于函数在区间((cfrac{1}{2},+infty))上单调递减,
故(f'(x)=cfrac{2a-1}{(2x-1)^2}leq 0)在区间((cfrac{1}{2},+infty))上恒成立,
即(2a-1leq 0)恒成立,得到(aleq cfrac{1}{2}),
但是当(a=cfrac{1}{2})时
代入原函数得到(f(x)=cfrac{1}{2}),为常函数,
则要舍去,故(a<cfrac{1}{2})。
法2:图像法,将函数变形为(f(x)=cfrac{-a+cfrac{1}{2}}{2x-1}+cfrac{1}{2}),
即函数的对称中心是((cfrac{1}{2},cfrac{1}{2})),
如果要函数在区间((cfrac{1}{2},+infty))上单调递减,
只需要(-a+cfrac{1}{2}>0)即可,故(a<cfrac{1}{2})。
(1).讨论函数(f(x))的单调性;
分析:用导数法求解,(f'(x)=3x^2-a) ,作出导函数的简图(三种代表情形),
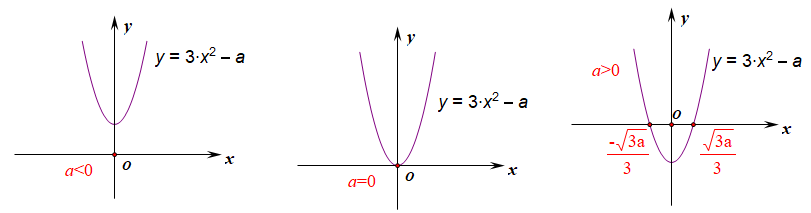
当(aleq 0)时,(f'(x)ge 0),故在((-infty,+infty))上单调递增;
当(a>0)时,令(f'(x)=0),得到(x=pm cfrac{sqrt{3a}}{3}),故(xin (-infty, -cfrac{sqrt{3a}}{3}))时,(f'(x)>0),(f(x) earrow);
(xin (-cfrac{sqrt{3a}}{3},cfrac{sqrt{3a}}{3}))时,(f'(x)<0),(f(x)searrow);(xin (cfrac{sqrt{3a}}{3},+infty))时,(f'(x)>0),(f(x) earrow);
(2).若函数(f(x))在(R)上是增函数,求(a)的取值范围。
分析:由于函数(f(x))在(R)上是增函数,即(f'(x)geqslant 0)在(R)上恒成立,且恒满足(f'(x) eq 0),即(f(x))不为常函数;
则(f'(x)=3x^2-ageqslant 0)恒成立,分离参数得到,
(aleqslant 3x^2)在(R)上恒成立,而((3x^2)_{min}=0),
则(aleqslant 0),又因为当(a=0)时,函数不为常函数,故参数(a)的取值范围是(ain (-infty,0])。