圆锥曲线题目中的运算训练

前言

在高中的教学实际中，涉及到圆锥曲线的定值、定点等问题的运算，难度都是相当高的，更不用说在初次接触题目时，我们对其运算的方向都可能是模糊不清的。不过本博文旨在重点练习与之相关的运算，探讨如何突破难点运算；

运算案例

【2017宝鸡中学高三理科第一次月考第22题】已知右焦点为(F)的椭圆(M：cfrac{x^2}{a^2}+cfrac{y^2}{3}=1(a>sqrt{3}))与直线(y=cfrac{3}{sqrt{7}})相交于(P)、(Q)两点，且(PFperp QF)。

(1). 求椭圆(M)的方程。（略）

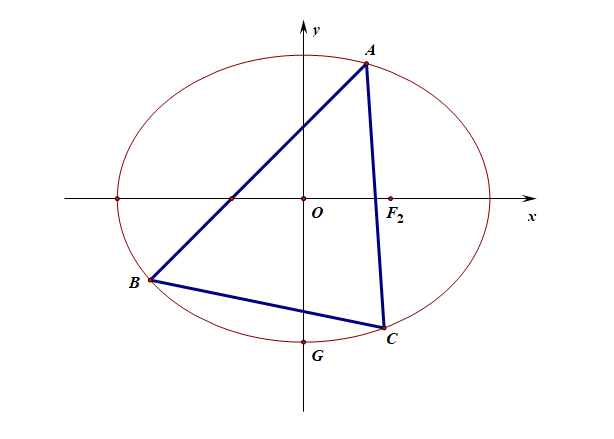
(2). (O)为坐标原点，(A)、(B)、(C)是椭圆(M)上不同三点，并且(O)是(Delta ABC)的重心，试探究(Delta ABC)的面积是否为定值，若是，求出这个定值；若不是，说明理由。

解析： (有斜率时)设直线 (AB) 的方程为 (y=kx+m)，即(kx-y+m=0)，

代入椭圆方程 (3x^{2}+4y^{2}=12)，

可得 ((3+4k^{2})x^{2}+8kmx+4m^{2}-12=0)，

设(A(x_{1}, y_{1}))， (B(x_{2}, y_{2}))，则(overrightarrow{OA}=(x_1,y_1))，(overrightarrow{OB}=(x_2,y_2))，

由韦达定理得到，则 (x_{1}x_{2}=cfrac{4m^{2}-12}{3+4k^{2}})， (x_{1}+x_{2}=-cfrac{8km}{3+4k^{2}})，

(y_{1}+y_{2}=k(x_{1}+x_{2})+2m=cfrac{6m}{3+4k^{2}})，

由 (O) 为 ( riangle ABC) 的重心， 则(overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}=overrightarrow{0})

可得 (overrightarrow{OC}=-(overrightarrow{OA}+overrightarrow{OB}))，又由于(overrightarrow{OA}+overrightarrow{OB}=(x_1+x_2,y_1+y_2))，

故有(overrightarrow{OC}=(cfrac{8km}{3+4k^{2}},-cfrac{6m}{3+4k^{2}}))，即点(C(cfrac{8km}{3+4k^{2}},-cfrac{6m}{3+4k^{2}}))

由于点(C)在椭圆上， 则有 (3(cfrac{8km}{3+4k^{2}})^{2}+4(-cfrac{6m}{3+4k^{2}})^{2}=12)，

化简上式，可得 4(m^{2}=3+4k^{2})，

又由弦长公式可得，(|AB|=sqrt{1+k^{2}}cdotsqrt{(x_{1}+x_{2})^{2}-4x_{1}x_{2}})

(=sqrt{1+k^{2}}cdotsqrt{(-cfrac{8km}{3+4k^{2}})^{2}-4cdotcfrac{4m^{2}-12}{3+4 k^{2}}})

(=cfrac{4 sqrt{1+k^{2}}}{3+4k^{2}}cdotsqrt{9+12k^{2}-3m^{2}})

再者，由点(C) 到直线 (AB) 的距离 (d=cfrac{|kx_{_C}+m-y_{_C}|}{sqrt{1+k^{2}}})

(=cfrac{left|kcdot cfrac{8km}{3+4k^{2}}+m-(-cfrac{6m}{3+4k^{2}}) ight|}{sqrt{1+k^{2}}}=cfrac{|3m|}{sqrt{1+k^{2}}})，

(S_{ riangle ABC}=cfrac{1}{2}|AB| cdot d=cfrac{1}{2}cdotcfrac{4sqrt{1+k^{2}}}{3+4k^{2}}cdotsqrt{9+12k^{2}-3m^{2}}cdot cfrac{|3m|}{sqrt{1+k^{2}}})

(=cfrac{6|m|}{3+4k^{2}}cdotsqrt{9+12k^{2}-3m^{2}})(=cfrac{6|m|}{4m^{2}}cdotsqrt{12m^{2}-3m^{2}})

(=cfrac{6|m|}{4m^{2}}cdot |3m|=cfrac{9}{2})，

当直线 (AB) 的斜率不存在时，要满足条件(overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}=overrightarrow{0})，

则直线为 (x=-1)，此时(A(-1,cfrac{3}{2}))，(B(-1,-cfrac{3}{2}))，(C(2,0))，

故 (|AB|=3)， (d=2+1=3)， (S_{ riangle ABC}=cfrac{1}{2}|AB|cdot d=cfrac{9}{2}).

综上可得， ( riangle ABC) 的面积为定值 (cfrac{9}{2}).

运算片段

将直线 (y=kx+m) 代入椭圆方程 (3x^{2}+4y^{2}=12)的化简；

化简过程：(3x^2+4(kx+m)^2=12)，

即(3x^2+4(k^2x^2+2kxm+m^2)-12=0)，

即(3x^2+4k^2x^2+8kxm + 4m^2- 12=0)，

即 ((3+4k^{2})x^{2}+8kmx+4m^{2}-12=0)；

化简 (3(cfrac{8km}{3+4k^{2}})^{2}+4(-cfrac{6m}{3+4k^{2}})^{2}=12)；

化简过程：(3cdotcfrac{64k^2m^2}{(3+4k^{2})^2}+4cdot cfrac{36m^2}{(3+4k^{2})^2}=12)

即(3cdot 64k^2m^2+4cdot 36m^2=12(3+4k^2)^2)

即(16k^2m^2+12m^2=(3+4k^2)^2)

即(4m^2(4k^2+3)=(3+4k^2)^2)

化简，可得 (4m^{2}=3+4k^{2})，

化简(|AB|=sqrt{1+k^{2}}cdotsqrt{(x_{1}+x_{2})^{2}-4x_{1}x_{2}})；

化简过程：上式(=sqrt{1+k^{2}}cdotsqrt{(-cfrac{8km}{3+4k^{2}})^{2}-4cdotcfrac{4m^{2}-12}{3+4 k^{2}}})

(=sqrt{1+k^{2}}cdotsqrt{cfrac{64k^2m^2}{(3+4k^{2})^2}-cfrac{4(4m^{2}-12)(3+4k^2)}{(3+4k^{2})^2}})

(=sqrt{1+k^{2}}cdotsqrt{cfrac{64k^2m^2-4(12m^2+16k^2m^2-36-48k^2)}{(3+4k^2)^2}})

(=cfrac{sqrt{1+k^2}}{3+4k^2}sqrt{-48m^2+4 imes36+48 imes4k^2})

(=cfrac{sqrt{1+k^2}}{3+4k^2}sqrt{-3 imes 16 m^2+4 imes4 imes9+4 imes4 imes3 imes4k^2})

(=cfrac{4sqrt{1+k^{2}}}{3+4k^{2}}cdotsqrt{9+12k^{2}-3m^{2}})

化简点线距；

点线距公式：(d=cfrac{|Ax_0+By_0+C|}{sqrt{A^2+B^2}})

则点(C) 到直线 (AB) 的距离(d=cfrac{|kx_{_C}+m-y_{_C}|}{sqrt{1+k^{2}}})

(=cfrac{left|kcdot cfrac{8km}{3+4k^{2}}+m-(-cfrac{6m}{3+4k^{2}}) ight|}{sqrt{1+k^{2}}})

(=cfrac{left|cfrac{8k^2m}{3+4k^{2}}+cfrac{3m+4k^{2}m}{3+4k^{2}}+cfrac{6m}{3+4k^{2}} ight|}{sqrt{1+k^{2}}})

(=cfrac{cfrac{|12k^2m+9m|}{3+4k^{2}}}{sqrt{1+k^2}}=cfrac{cfrac{|3m|(3+4k^{2})}{3+4k^{2}}}{sqrt{1+k^2}})

(=cfrac{|3m|}{sqrt{1+k^{2}}})，

化简面积公式的计算结果；

由前面可知， (4m^{2}=3+4k^{2})，故(9+12k^2=12m^2)，

故(S_{ riangle ABC}=cfrac{1}{2}|AB| cdot d)

(=cfrac{1}{2}cdotcfrac{4sqrt{1+k^{2}}}{3+4k^{2}}cdotsqrt{9+12k^{2}-3m^{2}}cdot cfrac{|3m|}{sqrt{1+k^{2}}})

(=cfrac{6|m|}{3+4k^{2}}cdotsqrt{9+12k^{2}-3m^{2}})(=cfrac{6|m|}{4m^{2}}cdotsqrt{12m^{2}-3m^{2}})

(=cfrac{6|m|}{4m^{2}}cdot sqrt{9m^2}=cfrac{6|m|}{4m^{2}}cdot |3m|=cfrac{9}{2})，

思维沉淀

如上例，探究(S_{ riangle ABC}=cfrac{1}{2} imes |AB| imes d)是否为定值，可能(|AB|=f(m,k))，或(d=g(m,k))，一开始别太担心引入的参数多，由题目中的某个条件，往往就能将其中的一个参数转化为用另一个参数表达，如本题中，(4m^2=3+4k^2)，这样，就可以将上述的(|AB|=f(m,k)=h(m))，(d=g(m,k)=l(m))，最后(S_{ riangle ABC}=cfrac{1}{2} imes h(m) imes l(m))，而由于乘法和分式的共同作用，导致包含参数的部分就整体约分，从而没有参数 (m)，这样整个结果就是个定值了。

当提炼出上述的思路模型，相应的我们对自己的运算也就有信心了。

新年快乐！