前言
两条共面直线所成的角的范围是: ([0,cfrac{pi}{2}]) ,两条异面直线所成的角的范围是 ((0,cfrac{pi}{2}]) .
求解思路
一般来说,常见的求解思路有两个。其一,转化法,具体做法,将两条异面直线中的一条平移到和另一条直线相交的位置,找到这两条相交直线所成的角或者其补角(必须保证其范围在 ((0,cfrac{pi}{2}]) 内),然后利用其所在的三角形来求解,此时可能用到余弦定理;其二,利用空间向量法求解。这一方法一般是理科学生要求掌握的,此时需要熟练掌握直线的方向向量,向量的内积公式,向量的坐标运算等 .
典例剖析
解析: 由于 (AD_{1}//BC_{1}), 所以 (angle PBC_{1}) 是直线 (PB) 与 (AD_{1}) 所成的角[或所成角的补角]准确的说法还需要添加这句话,或所成角的补角,原因是两条直线所成的角的范围是 ([0,cfrac{pi}{2}]) ,而图形中的角 (angle PBC_{1}) 的大小不一定在此范围内,
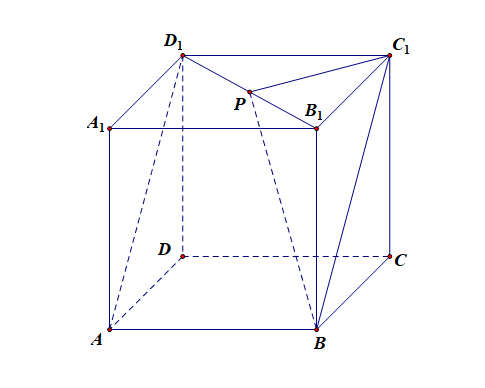
设正方体 (ABCD-A_{1}B_{1}C_{1}D_{1}) 的棱长为 (2),
则 (PB_{1}=PC_{1}=cfrac{1}{2}sqrt{2^{2}+2^{2}}=sqrt{2}),
(BC_{1}=sqrt{2^{2}+2^{2}}=2sqrt{2}), (BP=sqrt{2^{2}+(sqrt{2})^{2}}=sqrt{6}),
所以 (cosangle PBC_{1}=cfrac{PB^{2}+BC_{1}^{2}-PC_{1}^{2}}{2 imes PB imes BC_{1}}=cfrac{6+8-2}{2 imessqrt{6} imes2sqrt{2}}=cfrac{sqrt{3}}{2}),
所以,(angle PBC_{1}=cfrac{pi}{6}), 则直线 (PB) 与 (AD_{1}) 所成的角为 (cfrac{pi}{6}), 故选: (D) .
法1:立体几何法,基本求解步骤:①作:作出所要求的角;②证:证明所作的角即为所求的角;③算:计算所作角的某种三角值;
思路:将两条异面直线平移至一个三角形中,然后解三角形得到。
将(BC_1)平移到(AD_1),联结(CD_1),则(angle CAD_1)为两条异面直线所成的角,
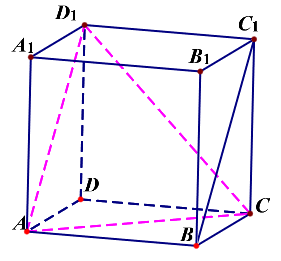
在(Delta ACD_1)中,可知(AC=sqrt{5}),(AD_1=sqrt{5}),(CD_1=2sqrt{2}),
由余弦定理可知(cosangle CAD_1=cfrac{(sqrt{5})^2+(sqrt{5})^2-(2sqrt{2})^2}{2cdot sqrt{5}cdot sqrt{5}}=cfrac{1}{5});
法2:空间向量法,
以点(D)为坐标原点,分别以(DA、DC、DD_1)所在的直线为(x、y、z)轴建立如图所示的直角坐标系,
则点(D(0,0,0)),(A(1,0,0)),(C(0,2,0)),(B(1,2,0)),(D_1(0,0,2)),(A_1(1,0,2)),(B_1(1,2,2)),(C_1(0,2,2)),
故(overrightarrow{BC_1}=(-1,0,2)),(overrightarrow{AC}=(-1,2,0)),
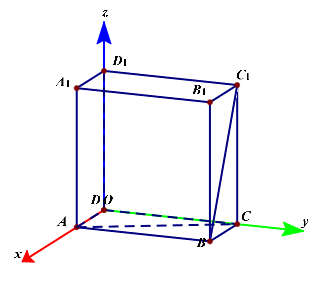
设两条异面直线所成的角为( heta),则(cos heta=|cos<overrightarrow{BC_1},overrightarrow{AC}>|=cfrac{(-1) imes(-1)+0 imes2+2 imes 0}{sqrt{(-1)^2+0^2+2^2} imessqrt{(-1)^2+2^2+0^2}}=cfrac{1}{5})。
备注:两条异面直线所成角的范围([0,cfrac{pi}{2}]),两个向量所成角的范围([0,pi])。
【法1-1】空间向量法,第一种建系方式;以点(A)为坐标原点,以(AC),(AA_1)分别为(y)、(z)轴,以和(AC)垂直的直线为(x)轴,建立如图所示的空间直角坐标系,
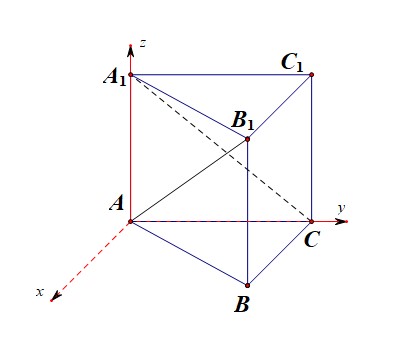
则(A(0,0,0)),(B(sqrt{3},1,0)),(A_1(0,0,2)),(B_1(sqrt{3},1,2)),(C(0,2,0)),
(overrightarrow{AB_1}=(sqrt{3},1,2)),(overrightarrow{A_1C}=(0,2,-2)),且线线角的范围是([0,cfrac{pi}{2}]),
故所求角的余弦值为(|cos<overrightarrow{AB_1},overrightarrow{A_1C}>|=cfrac{|1 imes 2+2 imes(-2)|}{sqrt{8} imessqrt{8}}=cfrac{1}{4})。故选(C)。
【法1-2】空间向量法,第二种建系方式;以(BN)的中点为坐标原点建立如图所示的空间直角坐标系,
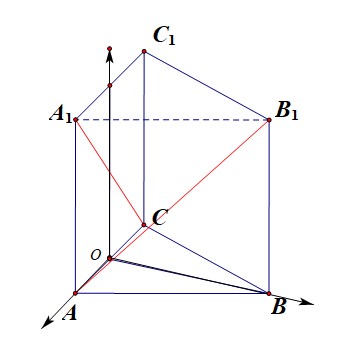
则(A(1,0,0)),(B(0,sqrt{3},0)),(C(-1,0,0)),(A_1(1,0,2)),(B_1(0,sqrt{3},2)),(C_1(-1,0,2)),
(overrightarrow{AB_1}=(-1,sqrt{3},2)),(overrightarrow{A_1C}=(-2,0,-2)),且线线角的范围是([0,cfrac{pi}{2}]),
故所求角的余弦值为(|cos<overrightarrow{AB_1},overrightarrow{A_1C}>|=cfrac{|-1 imes (-2)+sqrt{3} imes 0+2 imes(-2)|}{sqrt{8} imessqrt{8}}=cfrac{1}{4})。故选(C)。
【法2】:立体几何法,补体平移法,将正三棱柱补体为一个底面为菱形的直四棱柱,连结(B_1D),则(B_1D//A_1C),

故异面直线(AB_1)与(CA_1)所成角,即转化为共面直线(AB_1)与(B_1D)所成的角(angle AB_1D),连结(AD),
在(Delta AB_1D)中,(AB=AA_1=2),可得(AB_1=B_1D=2sqrt{2}),(AD=2sqrt{3}),
由余弦定理可知,(cosangle AB_1D=cfrac{(2sqrt{2})^2+(2sqrt{2})^2-(2sqrt{3})^2}{2 imes 2sqrt{2} imes 2sqrt{3}}=cfrac{1}{4}),
故所求为(cfrac{1}{4}),故选(C)。
分析:如图所示,直线(BD)与平面(ADD_1A_1)所成角的为(angle BDA),则由(tanangle BDA=2),可以设(AB=2k),(AD=k),则(BD=sqrt{5}k),直线(BD_1)与平面(ABCD)所成角的为(angle D_1BD),则由(sinangle D_1BD=cfrac{2}{3}),可以设(DD_1=2m),(BD_1=3m),则(BD=sqrt{5}m),
故可以令(m=k=1),则长方体的三维(AB=2),(AD=1),(DD_1=2),接下来的思路可以有两个:
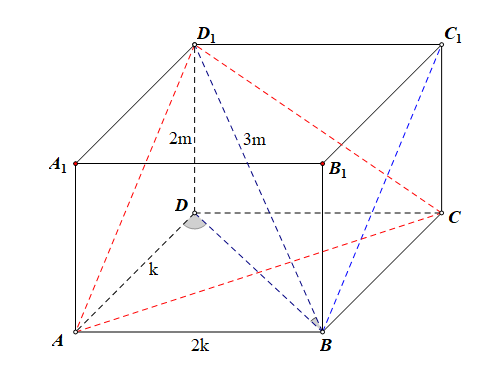
思路1:平移法,将异面直线(CD_1)与(BD_1)通过平移放置到同一个三角形( riangle AVD_1)中,这样(AC=sqrt{5}),(AD_1=sqrt{5}),(CD_1=2sqrt{2}),则异面直线(CD_1)与(BD_1)所成的角即为(angle AD_1C),由余弦定理可知(cos angle AD_1C=cfrac{sqrt{10}}{5}).故选(A).
思路2:空间向量法,不作平移,直接利用直线的方向向量的夹角来求解;
法1:空间向量法,如图所示,(PFperp)面(ABC),(F)为(Delta ABC)的中心,
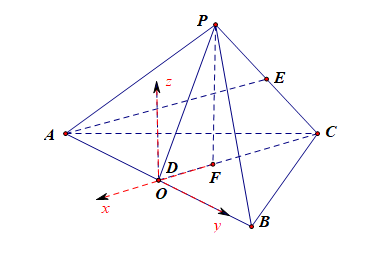
以点(D)为坐标原点,以(DF)、(DB)以及与(FP)平行的直线分别为(x),(y),(z)轴建立如图所示的空间直角坐标系,
令正四面体的棱长为(2),则得到以下点的空间坐标
(D(0,0,0)),(A(0,-1,0)),(B(0,1,0)),
(C(-sqrt{3},0,0)),(P(-cfrac{sqrt{3}}{3},0,cfrac{2sqrt{6}}{3})),(E(-cfrac{2sqrt{3}}{3},0,cfrac{sqrt{6}}{3})),
则有(overrightarrow{PD}=(cfrac{sqrt{3}}{3},0,-cfrac{2sqrt{6}}{3}));(overrightarrow{AE}=(-cfrac{2sqrt{3}}{3},1,cfrac{sqrt{6}}{3}));
令异面直线(PD)和(AE)的夹角为( heta),则有(cos heta)
(=cfrac{|cfrac{sqrt{3}}{3}cdot (-cfrac{2sqrt{3}}{3})+0cdot 1+(-cfrac{2sqrt{6}}{3}cdot cfrac{sqrt{6}}{3})|}{sqrt{(cfrac{sqrt{3}}{3})^2+(-cfrac{2sqrt{6}}{3})^2}cdot sqrt{(-cfrac{2sqrt{3}}{3})^2+1^2+(cfrac{sqrt{6}}{3})^2}}=cfrac{2}{3})。
说明:向量的夹角范围为([0,pi]),两异面直线的夹角范围([0,cfrac{pi}{2}])。
法2:立体几何法,先作再证后算。
思路:异面直线所成的角,一般是经过平移,使其相交,构建三角形来计算。
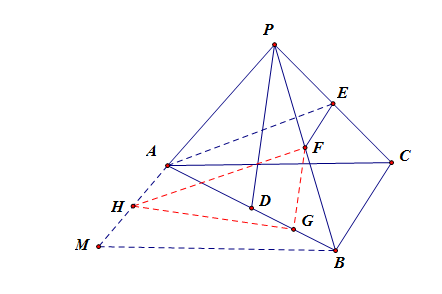
过点(A)做(AM//BC),过点(B)做(BM//AC)交(AM)于点(M),
点(F)、(H)、(G)分别是线段(PB)、(AM)、(BD)的中点,连接(HF)、(FG)、(HG),
则有 (EF;;{}_{=}^{//}AH) ,则(AE//FH),又(PD//FG),故(angle HFG)为两条异面直线所成的角。
设正四面体的棱长为(2),则(AE=FH=PD=sqrt{3}),(FG=cfrac{sqrt{3}}{2});
又在(Delta AHG)中,(AH=1),(AG=cfrac{3}{2}),(angle HAG=60^circ),
由余弦定理可知,(HG=cfrac{sqrt{7}}{2}),
在(Delta HFG)中,(HF=sqrt{3}),(FG=cfrac{sqrt{3}}{2}),(HG=cfrac{sqrt{7}}{2}),
由余弦定理可知(cosangle HFG=cfrac{2}{3})。
高阶例题
分析:由于求异面直线所成角的范围,故需要先明确其允许的最大范围,是((0,cfrac{pi}{2}]),怎么理解呢?采用简单原则,当同一平面内的两条直线相交时形成两对对顶角,其中的邻角互补,这样我们刻画其位置关系时,仅仅只需要([0,cfrac{pi}{2}])范围内的角就足够了,不需要范围为([0,pi]),那么异面直线所成角的范围就成了((0,cfrac{pi}{2}]),
再者我们需要将已知的直线安放在空间,最好的依托就是正方体和长方体等模型,如下图所示,

当异面直线(a),(b)所成的角为(cfrac{pi}{6}),直线(aperp c),那么异面直线(b)和(c)所成角的范围最小是(cfrac{pi}{2}-cfrac{pi}{6}=cfrac{pi}{3}),最大是(cfrac{pi}{2}+cfrac{pi}{6}=cfrac{2pi}{3}),又由于刻画异面直线所成角的范围限制,故只能是([cfrac{pi}{3},cfrac{pi}{2}]),故选(A)。

法1:理科学生可以使用建立空间直角坐标系的思路求解;
法2:平移构造三角形法,取(BC)的中点(F),连接(EF)和(AF),
则由(EF//PB),可知(angle AEF)即为两条异面直线(AE)与(PB)所成的角,
在( riangle AEF)中,容易知道(AE=EF=sqrt{2}),(AF=sqrt{3}),
由余弦定理可知,(cosangle AEF=cfrac{1}{4});

法1:几何法,通过作---证---算的步骤完成。
如图所示,取(AC)的中点(O),由于(AB=BC=3),故(BOperp AC),
在(Rt riangle ACD')中,(AC=sqrt{1^{2}+(sqrt{5})^{2}}=sqrt{6}),
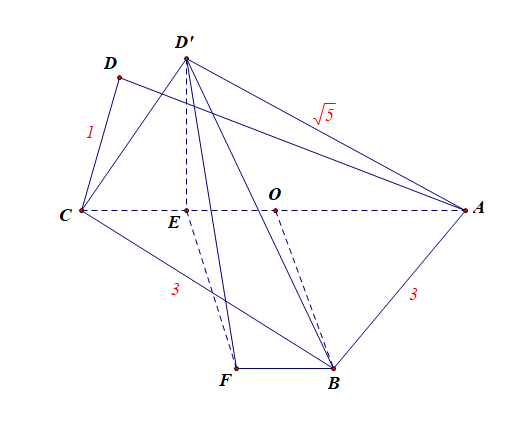
作 (D'Eperp AC),垂足为(E),(D'E=cfrac{1 imessqrt{5}}{sqrt{6}}=cfrac{sqrt{30}}{6}),
(CO=cfrac{sqrt{6}}{2}),(CE=cfrac{DC^{2}}{CA}=cfrac{1}{sqrt{6}}=cfrac{sqrt{6}}{6}),故(EO=CO-CE=cfrac{sqrt{6}}{3}),
过点(B)作(BF//AC),过点(E)作(EF//BO)交(BF)于点(F),则(EFperp AC),
连接(D'F),(angle FBD')为异面直线(AC)与(BD')所成的角求作异面直线所成的角,常用的方法是将其中的一条直线平移和另一条共面,此时这两条共面直线所成的角,即两异面直线所成的角。故两异面直线所成的角的范围为((0,cfrac{pi}{2}]),此题目中,由于(AC)//(BF),故(angle FBD')即异面直线(AC)与(BD')所成的角(quad),
则四边形(BOEF)为矩形,所以(BF=EO=cfrac{sqrt{6}}{3}),
(EF=BO=sqrt{3^{2}-(cfrac{sqrt{6}}{2})^{2}}=cfrac{sqrt{30}}{2}),
则(angle FED')为二面角 (D'-CA-B)的平面角,设为( heta),
则(D'F^{2}=(cfrac{sqrt{30}}{6})^{2}+(cfrac{sqrt{30}}{2})^{2}-2 imescfrac{sqrt{30}}{6} imescfrac{sqrt{30}}{2} imescos heta)
(=cfrac{25}{3}-5cos heta geqslant cfrac{10}{3}),当(cos heta=1) 时取等号,
故(BD')的最小值 (BD'_{min}=sqrt{cfrac{10}{3}+(cfrac{sqrt{6}}{3})^{2}}=2),
故直线(AC)与(BD')所成角(alpha)的余弦在(Rt riangle BFD')中,(cos)(alpha)(=)(cfrac{邻}{斜}),由于邻边(BF)长度不变,故斜边(BD')最小时,(cosalpha)的值最大;(quad)的最大值([cosalpha]_{max}=cfrac{BF}{BD'}=cfrac{frac{sqrt{6}}{3}}{2}=cfrac{sqrt{6}}{6})
法2: 也可以考虑使用空间向量法;