前言
高考中在压轴题中考查的函数有千千万,但是总能从其中找到一些比较核心的函数来;
常用函数
比如基本初等函数(f(x)=x)和(g(x)=e^x)做四则运算得到的这些函数:
(h(x)=xpm e^x);

(m(x)=xcdot e^x);(n(x)=cfrac{e^x}{x});(r(n)=cfrac{x}{e^x});
分析:若熟知上图的图像,分离参数,数形结合可得正确选项为(D)。

比如基本初等函数(f(x)=x)和(g(x)=lnx)做四则运算得到的这些函数:
(h(x)=xpm lnx);

(h(x)=xcdot ln^x);(h(x)=cfrac{lnx}{x});
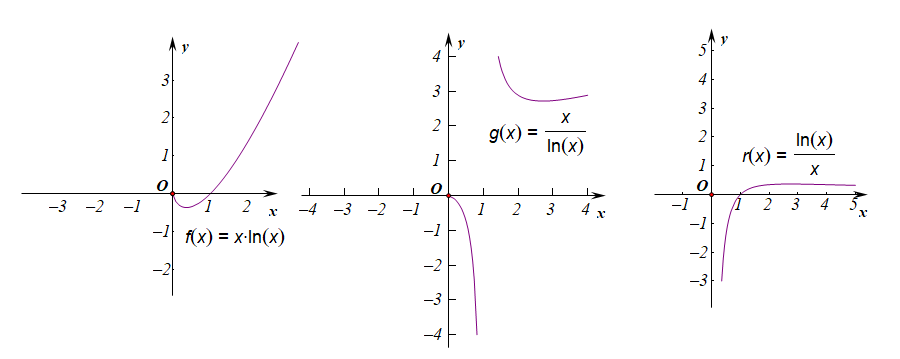
可以将他们作为导数工具的练习对象,熟练掌握他们的函数图像,有助于我们快速判断解题思路,作图时要注意因子(e^x)和(lnx);
常用不等式
- ①、(e^x>x+1(x eq 0))
证明思路:
【法1】数形结合法,令(f(x)=e^x),(g(x)=x+1),在同一个坐标系中作出这两个函数的图像,

由图像可知,当(x eq 0)时,都满足关系(e^x>x+1)。
补充:至于函数(f(x)=e^x)和函数(g(x)=x+1)为什么会相切与点((0,1)),
我们可以用导数方法来解答。
【法2】作差构造函数法,令(h(x)=e^x-x-1),则(h'(x)=e^x-1) ,
当(x<0)时,(h'(x)<0);当(x>0)时,(h'(x)>0);
即函数(h(x))在((-infty,0))上单调递减,在((0,+infty))上单调递增,
故函数(h(x)_{min}=h(0)=0),故(h(x)ge 0),当且仅当(x=0)时取到等号,
故(x eq 0)时,总有(h(x)>0),即(e^x>x+1)。
-
②、(e^xge x+1),注意没有(x eq 0)的条件限制。
-
③、(lnxleq x-1(x>0))
证明思路:【法1】数形结合法,令(f(x)=lnx),(g(x)=x-1),
在同一个坐标系中作出这两个函数的图像,
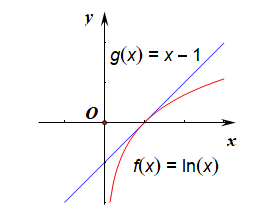
由图像可知,当(x> 0)时,都满足关系(lnxleq x-1)。
【法2】:作差构造函数法,令(h(x)=lnx-x+1(x>0)),则(h'(x)=cfrac{1}{x}-1),
当(0<x<1)时,(h'(x)>0);当(x>1)时,(h'(x)<0);
即函数(h(x))在((0,1))上单调递增,在((1,+infty))上单调递减,
故函数(h(x)_{max}=h(1)=0),故(h(x)leq 0),当且仅当(x=1)时取到等号,
故(x> 0)时,总有(h(x)leq 0),即(lnxleq >x-1)。
【法3】利用反函数法,此法主要基于(e^xge x+1)的结论,
由于函数(y=e^x)以及函数(y=x+1)关于直线(y=x)的对称函数
分别是(y=lnx)和函数(y=x-1),故得到(lnxleq x-1)。
【法4】:利用代数变换,由(e^xge x+1),两边取自然对数得到(lne^xge ln(x+1)),
即(xge ln(x+1)),再用(x-1)替换(x),得到(x-1ge lnx),即(lnxleq x-1)。
不等式的变形
- (e^xge x+1)的常见变形:
$e^xge x+1xrightarrow{用x+1替换x} e^{x+1}ge x+2 $
$Rightarrow e^{x+2}ge x+3 Rightarrow e^{x+n}ge x+n+1(nin N^*) $
(e^{frac{1}{3n}}>cfrac{1}{3n}+1(等号取不到))。
-
(e^x+2x-1ge 0)的解集,利用图像求解。转化为(e^xge 1-2x),做两个图像就能看出,解集为([0,+infty))
-
(e^x+kx-1ge 0(k>0))的解集,利用图像求解。转化为(e^xge 1-kx),做两个图像就能看出,解集为([0,+infty))
-
(lnxleq x-1(x>0))的常见变形:
(x+nge ln(x+n+1)(x eq 1))
(x-1> lnx xrightarrow{用cfrac{1}{x}替换x} cfrac{1}{x}-1> lncfrac{1}{x})
(Leftrightarrow cfrac{1-x}{x}>-lnx Leftrightarrow lnx>cfrac{x-1}{x}=1-cfrac{1}{x})。
(lncfrac{1}{x+1}leq cfrac{1}{1+x}-1(x>-1) Leftrightarrow (1+x)ln(1+x)ge x)
当(x>0)时,(ln(x+1)<x),故(cfrac{1}{x}ln(x+1)<1),
故(ln(x+1)^{cfrac{1}{x}}<1=lne),故((x+1)^{frac{1}{x}}<e),
将此结论应用到自然数得到((n+1)^{cfrac{1}{n}}<e),或者((1+cfrac{1}{n})^n<e)。
用(xRightarrow lnx),得到(xgeqslant lnx+1).
典例剖析
(1).对于(xin(0,1)),(f'(x)>0)恒成立,求实数(a)的取值范围。
分析:利用(cosx-a>0)在(xin(0,1))恒成立,可以求得(a<cos1)。
(2).当(a=1)时,令(h(x)=f(x)-sinx+lnx+1),求(h(x))的最大值。
分析:此时(h(x)=lnx-x+1),如果能知道结论(lnxleq x-1),
即可知(h(x)_{max}=h(1)=0)。或利用导数也可以求得(h(x)_{max}=h(1)=0)。
(3).求证:(ln(n+1)<1+cfrac{1}{2}+cfrac{1}{3}+cdots+cfrac{1}{n}(nin N^*))。
分析:看到这样的不等式关系,我们应该想到的有裂项相消法、数学归纳法,
法1: 由(2)的结论(lnx leq x-1)得到(ln(x+1)leq x(x eq 0)),
若将其延伸到自然数,则有(ln(n+1)<n),再做代换,
用(cfrac{1}{n})替换(n),变形得到(ln(cfrac{1}{n}+1)<cfrac{1}{n}),
即(ln(cfrac{n+1}{n})=ln(n+1)-lnn<cfrac{1}{n}),
令此式中的(n)分别取(1,2,3,cdots,n),即得到以下(n)个表达式:
(lncfrac{2}{1}<1);即(ln2-ln1<1)
(lncfrac{3}{2}<cfrac{1}{2});即(ln3-ln2<cfrac{1}{2});
(lncfrac{4}{3}<cfrac{1}{3});即(ln4-ln3<cfrac{1}{3});
(cdots);(cdots);
(lncfrac{1+n}{n}<cfrac{1}{n});即(ln(n+1)-lnn<cfrac{1}{n});以上式子累加,得到
(ln(n+1)-ln1<1+cfrac{1}{2}+cfrac{1}{3}+cdots+cfrac{1}{n}),
即(ln(n+1)<1+cfrac{1}{2}+cfrac{1}{3}+cdots+cfrac{1}{n}(nin N^*))。
法2:可以考虑用数学归纳法,待后思考。
证明:先用导数证明(e^xge x+1),再做代换,用(cfrac{1}{3^n})替换(x),
得到(e^{frac{1}{3^n}}>cfrac{1}{3^n}+1);即(1+cfrac{1}{3^n}<e^{cfrac{1}{3^n}});
故((1+cfrac{1}{3})cdot (1+cfrac{1}{3^2})cdot(1+cfrac{1}{3^3})cdots (1+cfrac{1}{3^n}))
(<e^{frac{1}{3}+frac{1}{3^2}+frac{1}{3^3}+dots+frac{1}{3^n}})
(=e^{cfrac{frac{1}{3}cdot[1-(frac{1}{3})^n]}{1-frac{1}{3}}})
(=e^{cfrac{1}{2}(1-cfrac{1}{3^n})}<e^{cfrac{1}{2}}=sqrt{e}<sqrt{4}=2),
故得证。