用导函数的图像判断原函数的单调性

前言

用导函数的图像判断原函数的单调性，其本质就是利用(f'(x))的正负，判断(f(x))的增减； 回顾：符号法则

典例剖析

• 给定(f'(x))的图像，确定(f(x))的单调性，最简单层次

如图是函数(y=f(x))的导函数(y=f^{prime}(x))的图像，则下面判断正确的是【 (quad)】

$A.$在区间$(一2,1)$上$f(x)$是增函数;

$B.$在区间$(1,3)$上$f(x)$是减函数;

$C.$在区间$(4,5)$上$f(x)$是增函数;

$D.$当$x=2$时，$f(x)$取到极小值

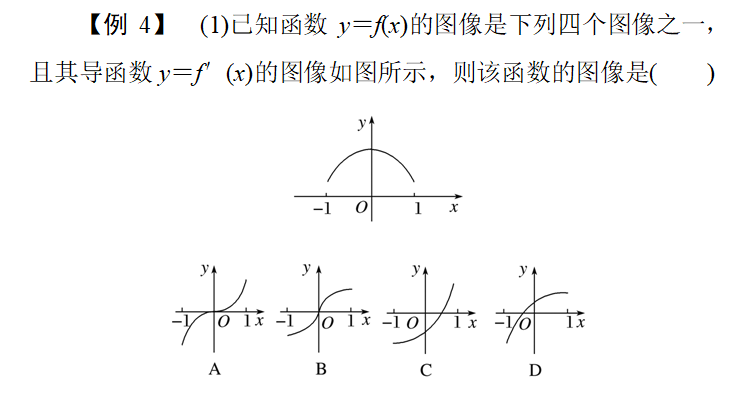
分析：本题目考查对导函数的图像的解读能力，和应用图像的意识；

由于在((4,5))上，有(f^{prime}(x)>0)恒成立，故(f(x))是增函数，故选(C).

• 用图像确定(f'(x))的正负，确定(f(x))的单调性，

【2017聊城模拟】已知函数(y=xf'(x))的图像如图所示(其中(f'(x))是函数(f(x))的导函数)，则下面四个图像中，(y=f(x))的图像大致是【】

分析：由图可知，

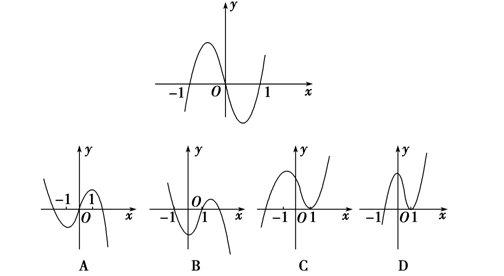
当(x<-1)时，(y<0)，故由符号法则可知(f'(x)>0)；

当(-1<x<0)时，(y>0)，故由符号法则可知(f'(x)<0)；

当(0<x<1)时，(y<0)，故由符号法则可知(f'(x)<0)；

当(x>1)时，(y>0)，故由符号法则可知(f'(x)>0)；

从而可知当(x<-1)时，(f'(x)>0)，(f(x) earrow)；

当(-1<x<1)时，(f'(x)<0)，(f(x)searrow)；

当(x>1)时，(f'(x)>0)，(f(x) earrow)；故选C。

【2017滨州模拟】设R上的可导函数(f(x))的导函数为(f'(x))，且函数(y=(1-x)f'(x))的图像如图所示，则下列结论一定成立的是【】

$A.$函数$f(x)$有极大值$f(2)$和极小值$f(1)$

$B.$函数$f(x)$有极大值$f(-2)$和极小值$f(1)$

$C.$函数$f(x)$有极大值$f(2)$和极小值$f(-2)$

$D.$函数$f(x)$有极大值$f(-2)$和极小值$f(2)$

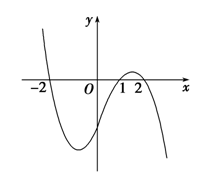
分析：当(x<-2)时，则有(1-x>0)，又(y>0)，故由符号法则可知(f'(x)>0)；

当(-2<x<1)时，则有(1-x>0)，又(y<0)，故由符号法则可知(f'(x)<0)；

当(1<x<2)时，则有(1-x<0)，又(y>0)，故由符号法则可知(f'(x)<0)；

当(x>2)时，则有(1-x<0)，又(y<0)，故由符号法则可知(f'(x)>0)；

从而可知当(x<-2)时，(f'(x)>0)，(f(x) earrow)；

当(-2<x<2)时，(f'(x)<0)，(f(x)searrow)；

当(x>2)时，(f'(x)>0)，(f(x) earrow)；故选(D)。

• 解不等式确定(f^{prime}(x))的正负，确定(f(x))的单调性，

【2017•合肥模拟】定义在(R)上的可导函数(f(x))的导函数为(f^{prime}(x))，已知函数(y=2^{f^{prime}(x)})的图像如图所示，则函数(y=f(x))的单调递减区间为【 】

$A.(1，+infty)$ $B.(1，2)$ $C.(-infty，2)$ $D.(2，+infty)$

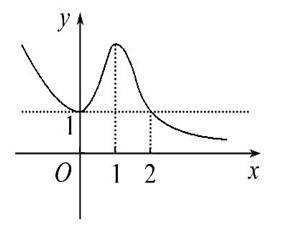
分析：结合图像可知，

当(xin(-infty，2])时，(2^{f^{prime}(x)}≥1)， 即(f^{prime}(x)≥0)；当(xin (2,+infty))时， (2^{f^{prime}(x)}<1)， 即(f^{prime}(x)<0)；

故函数(y=f(x))的递减区间为((2,+infty))。故选(D)。

(用不等式确定(f^{prime}(x))的正负，确定(f(x))的单调性)(2017•合肥模拟)

1、给定函数(y=(x^2-3x+2)cdot f'(x))的图像，先推断(f'(x))的正负，再确定(f(x))的单调性；

2、已知((x^2-3x+2)cdot f'(x)>0)，判断(f(x))的单调性；