scipy.stats.multivariate_normal的使用

参考：https://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.multivariate_normal.html

一个多元正态随机变量。
mean关键字指定平均值，cov关键字指定协方差矩阵。
新版本0.14.0。

补充：高斯分布

Gaussian Distribution(Normal Distribution)其图形特点为中间高，两头低，是钟形曲线(bell-shaped curve)。在高斯分布中，以数学期望μ(即mean)表示钟型的中心位置（也即曲线的位置），而标准差（standard deviation）σ表征曲线的离散程度。

协方差矩阵，参考百度百科：

协方差矩阵的每个元素是各个向量元素之间的协方差

协方差矩阵可用来表示多维随机变量的概率密度，从而可通过协方差矩阵达到对多维随机变量的研究

1）参数：

• x ： 数组，分位数，最后一个x轴标记组件。
• mean：数组，可选的。分布的均值（默认为0）
• cov ：数组，可选的。分布的协方差矩阵(默认为1)

可以该multivariate_normal对象可以被调用(作为函数)来固定均值和协方差参数，返回一个“frozen”的多元正态随机变量rv:

rv = multivariate_normal(mean=None, scale=1)

冻结对象采用相同的方法，但保持给定的均值和协方差不变。

2）注意：

将参数均值mean设为None等价于将均值mean设为零向量。参数cov可以是一个标量，在这种情况下，协方差矩阵是该值的单位乘、协方差矩阵的对角项向量，或者二维数组。

协方差矩阵cov必须是一个(对称的)正半定矩阵。将cov的行列式和逆分别计算为伪行列式和伪逆，使cov不需要满秩。

multivariate_normal的概率密度函数是：

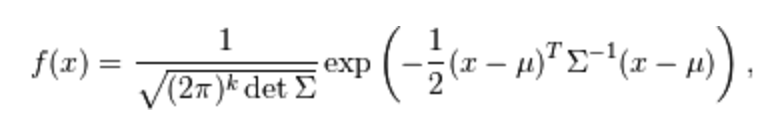
μ是平均值mean，默认为0；∑即cov是协方差矩阵，默认为1；k是x获取值的空间的维度

3）举例：

from scipy.stats import multivariate_normal
x = np.linspace(0, 5, 10, endpoint=False)
y = multivariate_normal.pdf(x, mean=2.5, cov=0.5);
x,y

返回，y得到的值x的值在mean=2.5取值点附近的可能性：

(array([0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5]),
 array([0.00108914, 0.01033349, 0.05946514, 0.20755375, 0.43939129,
        0.56418958, 0.43939129, 0.20755375, 0.05946514, 0.01033349]))

画图：

plt.plot(x, y)

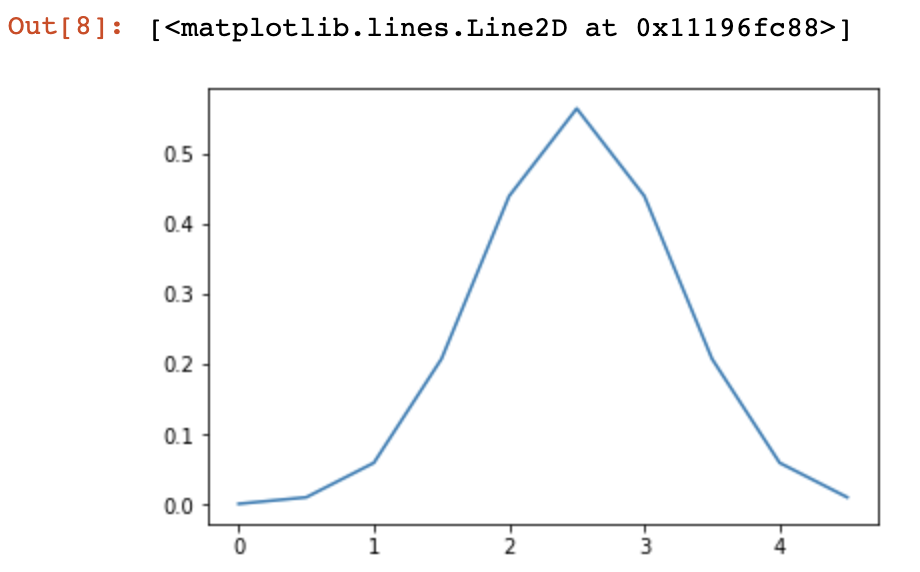
输入分位数x可以是任何形状的数组，只要最后一个轴标记组件。这使得我们可以在二维中显示非各向同性随机变量的冻结pdf,如下:

补充np.mgrid的用法

x, y = np.mgrid[-1:1:.01, -1:1:.01]
pos = np.empty(x.shape + (2,)) #从x.shape=(200,200)变为(200,200,2)
pos[:, :, 0] = x
pos[:, :, 1] = y
#mean=[0.5, -0.2],cov=[[2.0, 0.3], [0.3, 0.5]]，声明一个带着指定mean和cov的rv对象
rv = multivariate_normal([0.5, -0.2], [[2.0, 0.3], [0.3, 0.5]])
#将f(X,Y)=rv.pdf(pos)的值对应到color map的暖色组中寻找(X,Y)对应的点对应的颜色
plt.contourf(x, y, rv.pdf(pos))

返回：

可见使用概率密度函数pdf对数据pos，即(x,y)值进行处理后得到满足设置的mean和cov的值,使其分布满足高斯分布。rv.pdf(pos).shape为(200,200)

4)可使用方法：

• pdf(x, mean=None, cov=1) ：概率密度函数
• logpdf(x, mean=None, cov=1) ：概率密度函数日志
• rvs(mean=None, cov=1) ：从多元正态分布中随机抽取样本
• entropy() ：计算多元法线的微分熵