论文下载:http://openaccess.thecvf.com/content_cvpr_2017/papers/Liu_SphereFace_Deep_Hypersphere_CVPR_2017_paper.pdf
SphereFace: Deep Hypersphere Embedding for Face Recognition
softmax损失仅仅能够学到分辨性不够强的特征,除此之外,还有contrastive loss,center loss,triplet loss。
但是它们都在一定程度上存在弊端:
- center loss仅能使得类内紧凑,无法使得类间可分。
- contrastive loss和triplet loss需要pair/triplet 挖掘过程,增加时间的损耗。
- 除此之外,还有一个更关键之处:以上的损失函数都使用了欧式距离,而softmax损失学习到的特征有角度上的分布特性。
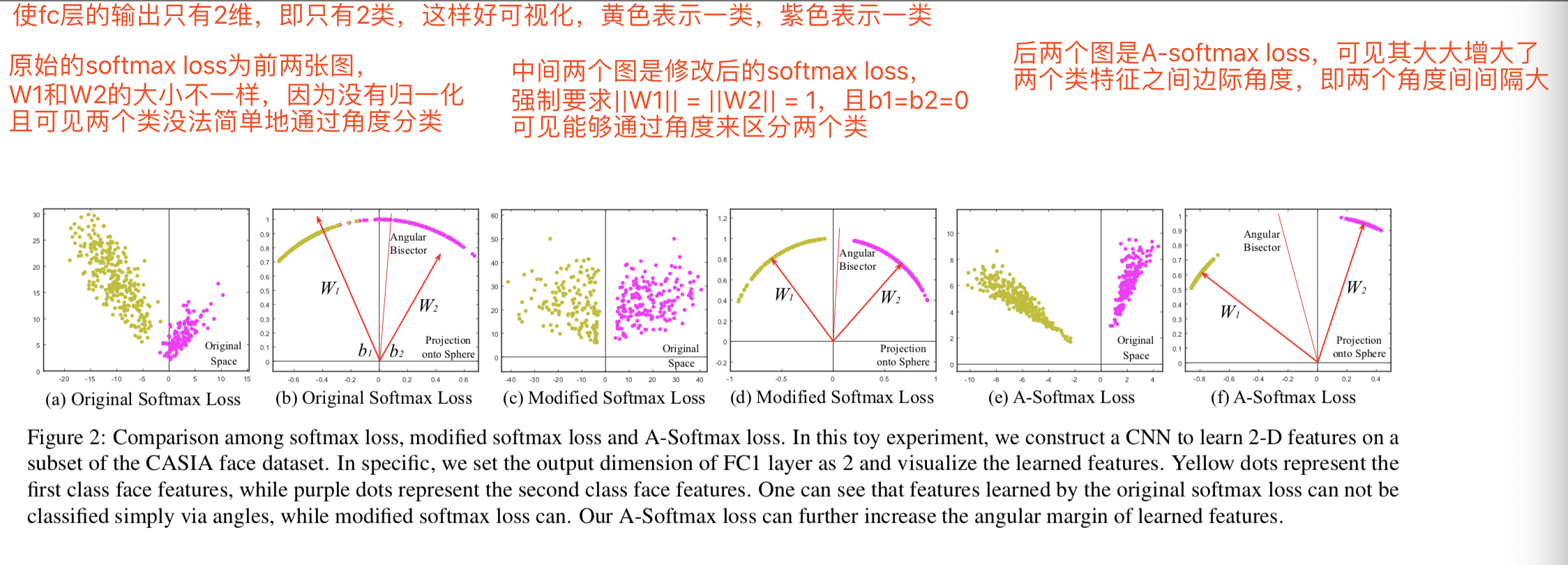
证明了softmax损失学习到的特征有角度上的分布特性,因此在这种意义上,欧式距离与softmax损失是不兼容的,所以作者认为结合softmax损失和欧式距离效果可能不是最佳的。
一步步修改损失:
1)modified softmax loss
传统softmax loss损失函数为:
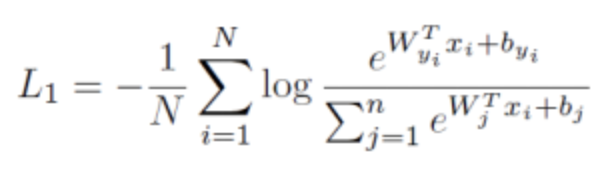
为了简化计算,把偏置b设置为0,,然后权重和输入的内积用下面式子表示:
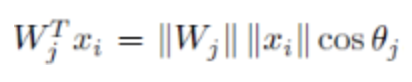
因此为了将损失函数变换成仅受角度影响的公式,需要经过下面的几个变换:
1》决策边界
首先softmax loss的决策边界(decision boundary)为:
(W1 −W2)x + b1 − b2 =0
其中W1、W2表示的是对应的权重矩阵中1、2对应的类的那一行;b1、b2同理;x即整个input输入的特征向量
这个公式是因为其决策边界是线性的。
证明:
假设决策边界是线性的,那么会有:

1.首先在决策边界上softmax对任意两类的输出概率是相等的。即对如上图的任一边界上的一点,softmax输出的概率向量上,该点被判断为边界两侧的类的对应分量是相等的
这样,通过计算可知:
zi = Wi*x + bi = zj = Wj*x + bj (这里Wi和Wj是权重矩阵第i,j行,i、j即边界两侧的两个类)
2.边界是线性的等价于边界上的任意两个点X1、X2,他们的线形组合X0=t*X1+s*X2 仍然在决策边界上,这里t+s=1
根据上面这两个条件证明:
从softmax的决策边界上任取两点X1,X2
由上面的叙述1可知,W1*x+b1=W2*x+b2,即(W1-W2)*x=b2-b1
再任取一点X0 = t*X1 + s*X2,s+t = 1
则softmax对X0的计算得z1 = W1*X0 + b1, z2 = W2*X0 + b2, 下面证明z1=z2:
z1 - z2 = W1*X0 + b1 - (W2*X0 + b2) ,(代入X0 = t*X1 + s*X2)
= t*(W1 - W2)*X1 + s*(W1 - W2)*X2 + (b1 - b2) ,(代入(W1-W2)*x=b2-b1)
= t*(b2-b1) + s*(b2-b1) + (b1-b2)
= 0
所以,z1=z2,即证明X0也在决策边界上
2》约束条件
然后使用L2正则化处理Wj使得||Wj||=1,L2正则化就是将Wj向量中的每个值都分别除以Wj的模,从而得到新的Wj,新的Wj的模就是1:
说明该方法只归一化了权重,而没有归一化特征向量

这样根据式子:
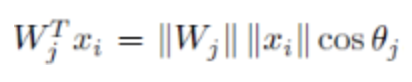
可以将softmax loss损失函数变换为只与角度相关的公式:
||x|| (cos(θi) - cos(θj)) = 0
这里的θi是Wi和x之间的角度
通过这样的损失函数学习,可以使得学习到的特征具有更明显的角分布,因为决策边界只与角有关
这样修改后的损失函数modified softmax loss为:

xi表示第i个训练样本,yi为第i个训练样本的类别,Wj表示W的第j列,Wyi表示W的第yi列,表示列是因为进行了转置
2)A-softmax loss(angular softmax)
1》添加定量控制参数m
添加一个定量控制参数m(m>=1)到决策边界上,这样类1和类2的决策边界为:
||x|| (cos(mθ1) - cos(θ2)) = 0, 对于类1来说
和 ||x|| (cos(θ1) - cos(mθ2)) = 0, 对于类2来说
m参数用来定量控制角度边际
在modified softmax loss,对于一个来自类别1 的可学习特征向量x,θi是该x和Wi之间的角度,可知如果我们希望网络能够分类得到该x属于类别1,那么就需要cos(θ1) > cos(θ2), 因为θi范围为[0,Π],在这个范围内cos()函数是递减的,所以要求(θ1) < (θ2)
所以如果增加一个参数m,变为cos(mθ1) > cos(θ2) , m >= 2 ,那么就希望训练得到的θ1更小,该类1的决策边界为cos(mθ1) = cos(θ2);同理cos(θ1) < cos(mθ2),也是希望训练得到的θ2更小,该类2的决策边界为cos(θ1) = cos(mθ2)。这样两个类的分布中间就会隔着一个比较大的角度边际,因为各自的角度都要乘以m才能到达边界
假设所有训练样本都正确分类了,那么决策边界将生成一个角度边际为(m−1/m+1)θ,即两个类的类间角度特征距离, θ是表示两个类的权值W1,W2之间的夹角。证明:
对于类别1,cos(mθ1) = cos(θ2), θ = θ1 + θ2
所以cos(mθ1) = cos(θ - θ1)
所以 mθ1 = θ - θ1
所以 θ1 = (1/m+1) θ
同理,对于类别2,cos(θ1) = cos(mθ2), θ = θ1 + θ2
所以cos(mθ2) = cos(θ - θ2)
所以 mθ2 = θ - θ2
所以 θ2 = (1/m+1) θ
所以最后计算两个类边界的角度为 θ - θ1 - θ2 = (m−1/m+1)θ
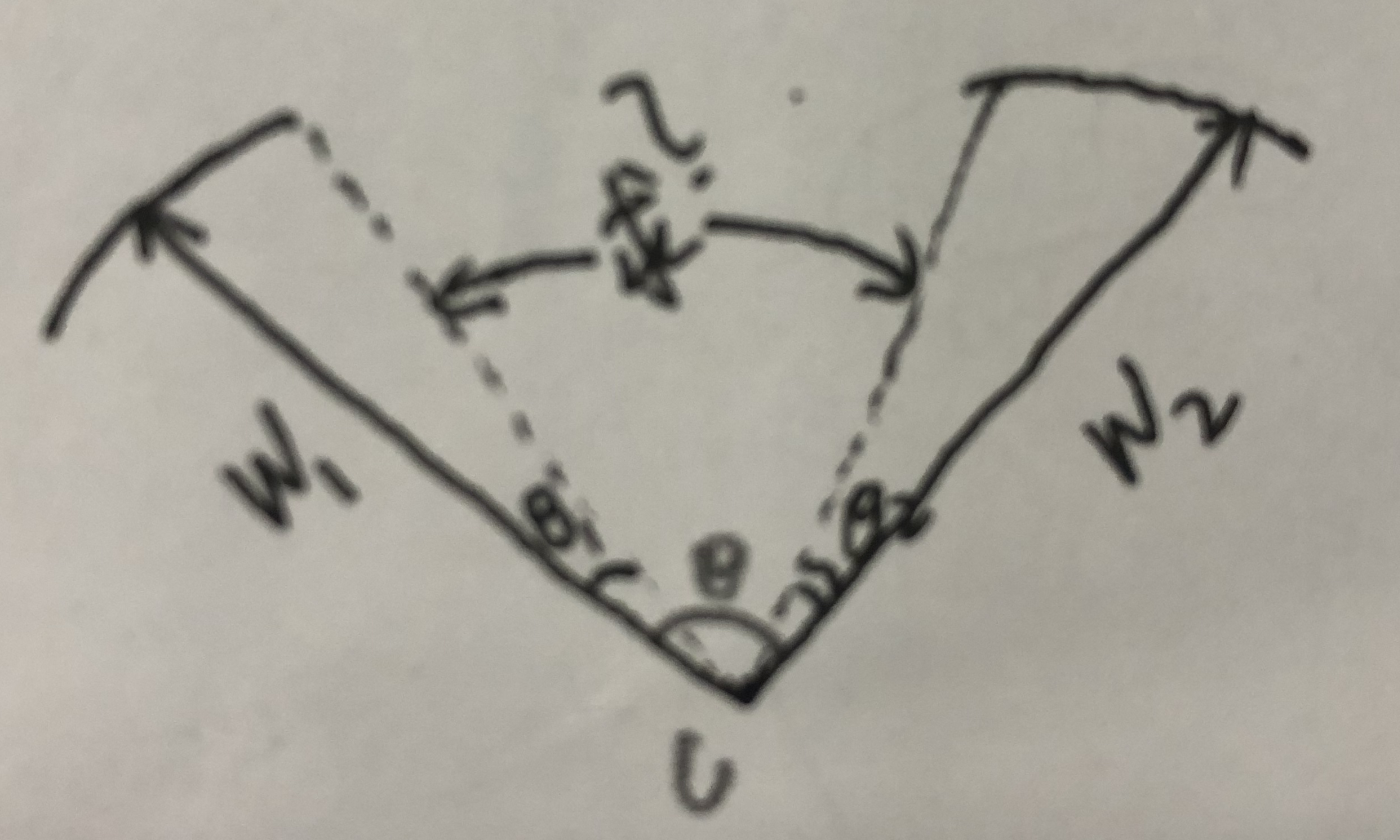
这样对于类型1,需要训练θ1< θ2/m;这样对于类型2,需要训练θ2 < θ1/m。这样肯定是比原始softmax loss的训练θ1< θ2和θ2 < θ1要难的
现在的损失函数为:
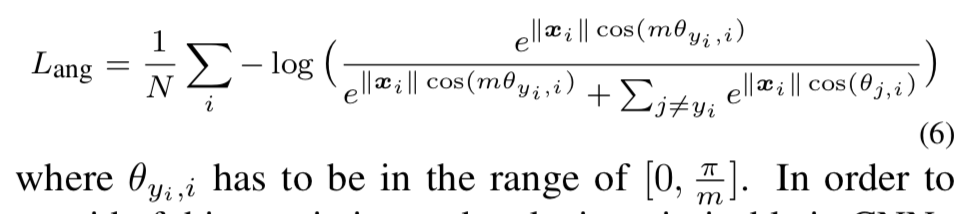
2》 定义新角度函数
为了摆脱这个角度的限制,通过概括一个单调递减的角度函数ψ(θyi,i)来扩展cos(θyi,i)的定义范围,在[0,π/m]的范围中两个函数是等价的,这样最终的损失为:

其中将 ψ(θyi,i)函数定义为:

![]()
m >= 1是用来控制角度边际大小的。当m=1时,该损失函数就等价与了modified softmax loss
可见

根据上面的式子画图:
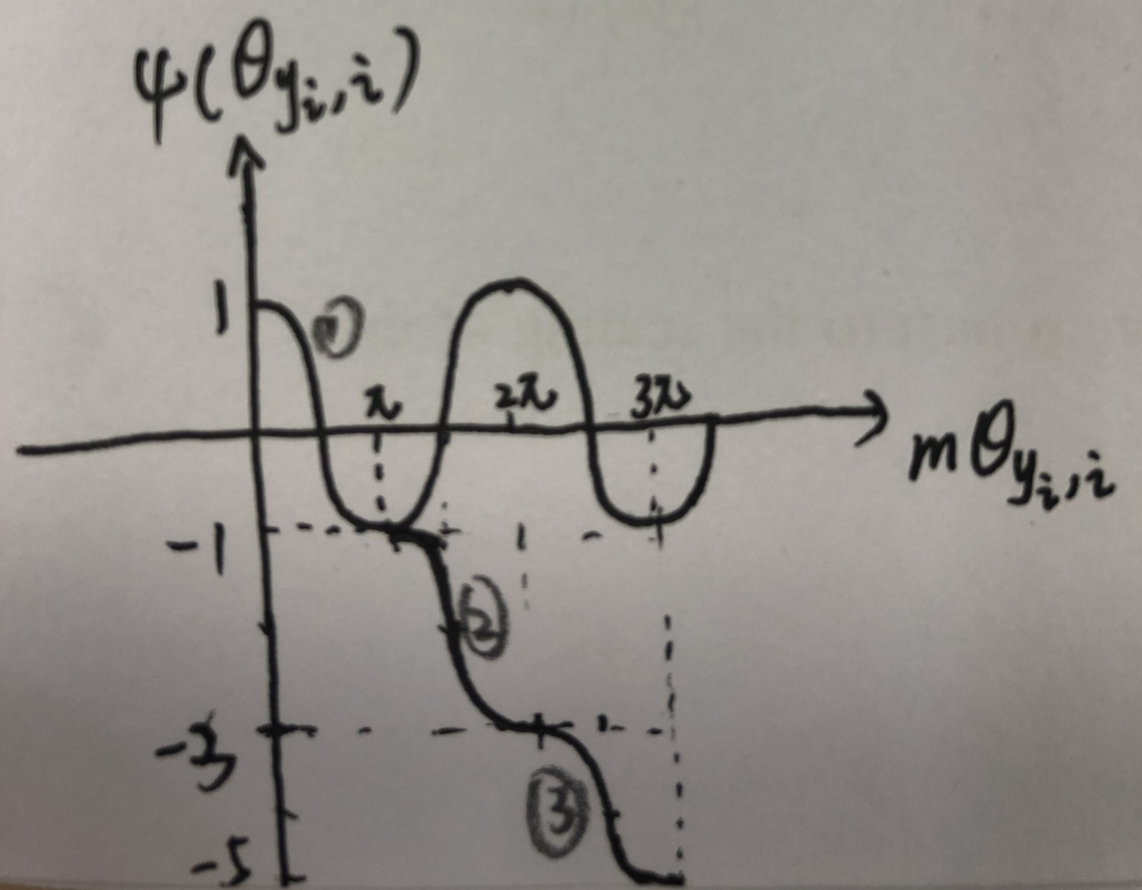
可见该函数是单调递减的
然而, SphereFace 的实现中整合了 Softmax 监督以保证训练的收敛,并且权重由动态超参数 λ
λ 控制。加入额外的 Softmax 损失,所以ψ(θyi,i)实际上是:
其中 λ是一个额外的超参数,以利于 SphereFace 的训练。λ在开始时设置为1,000,并且减少到5以使每个类的角度空间更紧凑。这个额外的动态超参数 λ使得 SphereFace 的训练相对棘手。
3》 该A-softmax loss的属性
属性1 :A-Softmax Loss定义了一个大角度间隔的学习方法,m越大这个间隔的角度(m−1/m+1)θ也就越大,相应区域流形的大小(θ1和θ2)就越小,这就导致了训练的任务也越困难。
定义1:定义mmin, 即当m>mmin时,类内的最大角度特征距离小于类间的最小角度特征距离
属性2 :在2分类问题中,mmin > 2 + √3
属性3: 在多分类问题中,mmin >= 3