算法笔记-贪心算法

贪心算法：保证每一步都是最优，最终结果肯定是最优的（简化了很多问题，不需要你有大局观）

场景：求集合的极限值（最多，最短，最便宜等等等...）

（1）会议安排

　　说明：在有限的时间内召开更多的会议，任何两个会议不能有时间冲突。下图是会议详情：

 　　思路：下一个会议要取结束时间最早的（更优的会议持续时间最短，相当于动态的改变开始时间）

 　　代码：

<?php
$meetings = [
    '1' => [3, 6], '2' => [1, 4], '3' => [5, 7], '4' => [2, 5], '5' => [5, 9],
    '6' => [3, 8], '7' => [8, 11], '8' => [6, 10], '9' => [8, 12], '10' => [12, 14],
    ];

//根据结束时间排序
uasort($meetings, function($p1, $p2){
    if ($p1[1] == $p2[1]) return 0;
    return $p1[1] > $p2[1] ? 1 : -1;
});

//取不冲突
$last = null;
foreach ($meetings as $k => $meet) {
    if (($last === null) || ($last !== null && $meet[0] >= $last))
        list($res[], $last) = [$k, $meet[1]];   
}

（2）最短路径

　　说明：景区有五个点，求第1个点到其他所有点的最短距离。地图如下：

 　　思路：依次找最近的点。大致过程如下：

　　　　　当前在1：得知1-2路程为2；1-3路程为5 。下面去2和3（因为1的两个出度分别是2和3）

　　　　　然后去2：得知2-4路程为6；2-3路程为1；  结合上面新得出的路程：1-3路程为4（1-2-3，要比上面的5小，这里要刷新一下），1-4路程为6（这个分支下面要去3和4）

　　　　   然后去3：得知 3-4路程为7；3-5路程为1； 结合上面新得出的路程：1-4路程还是4,1-5路程为5（1-2-3-5）（这个分支下面要去4和5）

　　　　  依次类推...

　　代码：

<?php
$map = [                                                                        //这里用矩阵表示地图
    [null, 2, 5, null, null],
    [null, null, 2, 6, null],
    [null, null, null, 7, 1],
    [null, null, 2, null, 4],
    [null, null, null, null, null],
];
$position = $start = 0;
$been = [];     //去过的点

function minPath($position)
{
    global $map, $start, $been;
    static $res = [];                                                           //结果
    $been[] = $position;                                                        //记录走过的点
    $next = [];
    foreach ($map[$position] as $k => $v) {
        if ($v !== null) {
            if (! isset($res[$start . $k]) || ($res[$start . $k] > $res[$start . $position] + $v)) {
                $res[$start . $k] = $res[$start . $position] + $v;              //记录最短的距离
                if (in_array($k, $been)) $next[] = $k;                          //这里放在后面解释
            }
            ! in_array($k, $been) && $next[] = $k;                              //记录接下来要走的点
        }
    } 
    
    foreach ($next as $v) {                                                     //接着找下个点
        minPath($v);
    }
    return $res;
}
$res = minPath($position);

　　　补充：代码第22行注释：

　　　　刚开始也没发现这个问题，执行上面的案例也没啥问题。但执行下面这个案例就有问题了（假如没有第22行）。走到第2个点的时候，还判定1-2的距离为8，所以计算1-4为9。等后来走到第3个点，把1-2的距离精确到3，但已经晚了。第2个点已经走过一次，不会再走了。也就是说不会再更新1-4的距离。所以当检测出距离更精确的时候（1-3-2比1-2要近），把那个点（第2个点）从记录走过点的数组中移除，重新在走一次。

　　　　或者可以手动遍历一下结果，将需要精确的精确一下，比如当发现1-3-2要比1-2要近，则更新1-2-4（第2个点的所有出度）。但这里要记录路径（只记录1-4=9不行，要记录1-2-4=9），性能应该要比上一个好很多。

　　

 （4）最小生成树

　　说明：把所有点都连接起来（从一点可以到任意一点），并且所有路径的和最小。地图如下：

　　思路：找到与初始点（管它叫a）最近的点（管它叫b），连接ab；　

　　　　　找到与a或b最近的点（管它叫c），连接bc（假如c和b最近）

　　　　　找到与a或b或c最近的点（管它叫d），连接ad（假如d和a最近）

　　　　　一直找完所有的点.....

　　代码：

<?php
$map = [                                                                        //要保证其是个连通图
    [null, 23, null, null, null, 28, 36],
    [23, null, 20, null, null, null, 1],
    [null, 20, null, 15, null, null, 4],
    [null, null, 15, null, 3, null, 9],
    [null, null, null, 3, null, 17, 16],
    [28, null, null, null, 17, null, 25],
    [36, 1, 4, 9, 16, 25, null],
];

function minTree($position)
{
    global $map;
    $distance = 0; $paths = []; $res[] = $position;
    while(true) {
        $minLink = ['from' => null, 'name' => null, 'value' => INF];
        foreach ($res as $p) {
            foreach ($map[$p] as $k => $v) {
                if ($v && $v < $minLink['value'] && ! in_array($k, $res)) {
                    $minLink = ['from' => $p, 'name' => $k, 'value' => $v];     //所有已知点遍历一遍，找到离已知点最近的点
                }
            }             
        }
        if ($minLink['name'] !== null) {                                        //收录新的已知点，并记录路径和长度
            $res[] = $minLink['name'];
            $paths[] = $minLink['from'] . $minLink['name'];
            $distance += $minLink['value'];
        } else {
            break;                                                              //全部走完可以结束了
        }
    }
    
    return [$paths, $distance];    
}

$position = 0;                                                                  //初始点随便选，路径方法可能答案不唯一，但总长度是唯一的
list($paths, $distance) = minTree($position);                                   //57

 （5）哈夫曼编码

　　说明：根据字母出现的频率，为其分配相应长度的编码（频率越高，编码越短），以下几个字母出现的频率如图：

 　　思路：把这些字母放到二叉树上，然后用01表示，频率较高的字母靠上。过程如下，不停的取出数组中最小的两个元素加和（和是父节点，这两个元素分别为左右叶）之后再放回数组中，直到剩下最后一个元素：

 

 

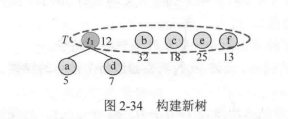
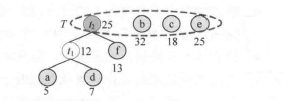
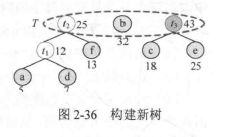
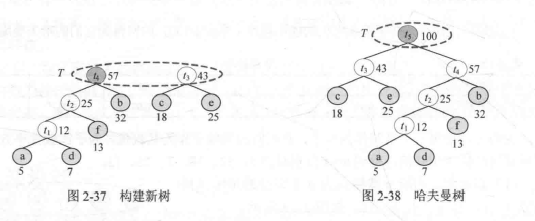
 代码：

<?php
$arr = [5, 32, 18, 7, 25, 13];

function createTree($arr)
{
    sort($arr);
    $arr[] = INF;                                                               //如果加和之后值在数组中最大，就不会插入了
    while (count($arr) > 2) {
        $left = gettype($arr[0]) == 'object' ? $arr[0] : newNode($arr[0]);
        $right = gettype($arr[1]) == 'object' ? $arr[1] : newNode($arr[1]);     //左右叶
        $set = newNode($left->name + $right->name, $left, $right);              //父节点
        unset($arr[0], $arr[1]);                                                //去除前两个元素
        foreach ($arr as $k => $v)
        {
            if ($set->name <= $v) {
                array_splice($arr, $k - 2, 0, [$set]);                          //插入加和的元素(每次会重置键值)
                break;
            }
        }
    }
    return $arr[0];
}

function newNode($name, & $left = null, & $right = null)
{
    $n = new stdClass();
    list($n->name, $n->left, $n->right, $n->parent) = [$name, & $left, & $right, null];
    $left && $left->parent = & $n;
    $right && $right->parent = & $n;
    return $n;
}
createTree($arr);