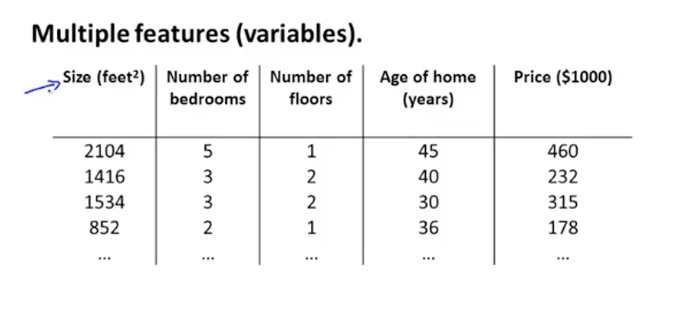
(1)说明:需要预测房屋的价格,除了房屋面积还有其他的特征量,比如层数,年龄,卧室数目等等,如下图。因为有多个特征值,所以称为多变量线性回归。
(2)假设函数:单变量只有一个特征值,所以之前的假设函数将不再适用,下面是多变量的假设函数。其中x0设置为1
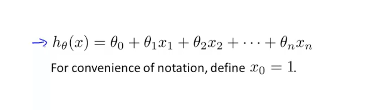
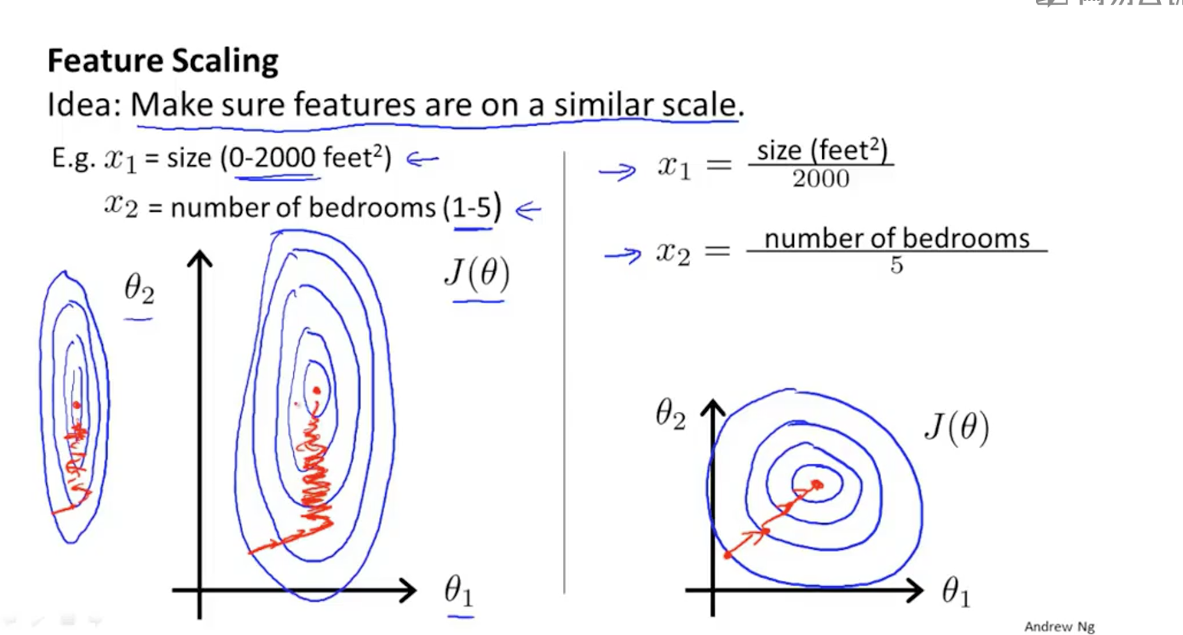
(3)特征缩放:在所有特征值中,size的范围大概在0~2000,而卧室数目的范围在0~5。如果多个参数之间范围跨度相差太大,将导致梯度下降的速度很缓慢。下面是关于这两个特征值的等高线。如图中左图案,红线表示梯度下降的大概路线,最理想的图像应该趋近于一个圆,范围跨度相差越大,图形越扁,梯度下降越慢。所以要进行特征缩放。特征缩放的公式不仅有一个,但目的都是将不同特征值缩放到一个相近的范围。右图是进行特征缩放之后的等高线。他的缩放方式就是将每个特征值除以该特征值的范围
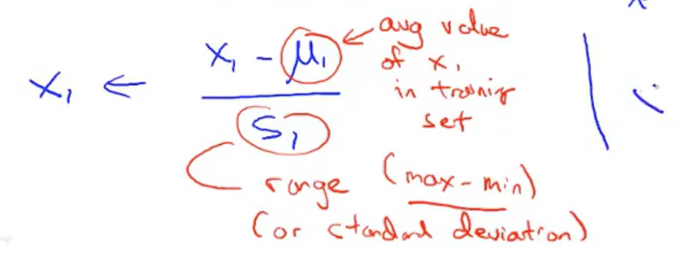
下面是特征缩放公式:u表示平均值,s表示该特征值的范围(max-min),s也可以替换为标准差。在根据特征缩放之后的数据计算出公式之后,用该公式对数据进行预测,数据不能直接适用,需要按照之前特征缩放的方式就行下处理才可以进行预测。或者根据特征缩放的方式对参数就行化简,之后数据可以直接拿来使用。就是下面的build函数
(4)代价函数:因为假设函数不同,代价函数变化如下图:上面是代价函数,下面是求偏导之后。

(5)梯度下降代码:
#coding=utf-8 import numpy as np np.set_printoptions(suppress=True) #特征缩放 def scale(arr): param = [] for i in range(0, arr.shape[1]): col = arr[:,i] mean = np.mean(col) std = np.std(col) param.insert(i, {'mean':mean, 'std':std}) for j in range(0, len(col)): arr[j][i] = (col[j] - mean) / std return arr, param #代价函数 def J(): global p, x_data, y_data, m, a deviation = np.dot(x_data, p).T - y_data return (np.dot(deviation, x_data) / m * a) #整理函数 demo:[(x1 - 10250) / 3269.17] * 13274.7755 + [(x2 - 69.5) / 14.22] * 10568.71 + 55438.25 def build(p, param): f = 0 #常数项 for i in range(1, len(p)): f -= param[i - 1]['mean'] / param[i - 1]['std'] * p[i][0] p[i] = format(p[i][0] / param[i - 1]['std'], '0.2f') p[0] = format(f + p[0][0], '0.2f') return p x_data = np.array([ [6000, 58], [9000, 77], [11000, 89], [15000, 54], ]) y_data = np.array([[30000, 55010, 73542, 63201]]) x_data = x_data.astype(np.float) x_data, param = scale(x_data) #学习率 a = 0.1 #x新增一列全为1 m = len(x_data) x_data = np.c_[np.ones(m), x_data] p = np.ones([3, 1]) #梯度下降 step = 300 for i in range(1, step): j = J() p -= j.T p = build(p, param)
(6)直接使用python函数库
#coding=utf-8 from sklearn.linear_model import LinearRegression x_data = [ [6000, 58], [9000, 77], [11000, 89], [15000, 54] ] y_data = [ 30000, 55010, 73542, 63201 ] lr = LinearRegression() lr.fit(x_data, y_data) p = [round(lr.intercept_, 2), round(lr.coef_[0], 2), round(lr.coef_[1], 2)]
(7)正规方程:相比于梯度下降,正规方程是个更简单的方法,直接套用公式就行。

(8)正规方程与梯度下降的优缺点:①正规方程不需要设置学习率
②正规方程不需要反复迭代
③梯度下降可以在特征量很多的情况下还可以正常工作,但正规方程不可以。大致边界在10000个特征量。

(9)正规方程代码:
#coding=utf-8 import numpy as np np.set_printoptions(suppress=True) x_data = np.array([ [6000, 58], [9000, 77], [11000, 89], [15000, 54], ]) y_data = np.array([[30000, 55010, 73542, 63201]]) m = len(x_data) x_data = np.c_[np.ones(m), x_data] x_data = x_data.astype(np.float) # p = np.linalg.pinv(np.dot(x_data.T, x_data)) p = np.dot(p, x_data.T) p = np.dot(p, y_data.T)
(10)多元多变量线性回归:比如预测一个房屋的价格,有两个特征量为房屋的长和宽。如果假设函数选为y=p0 + p1*x1 + p2*x2就不是很合适。正确的假设函数应为y=p0 + p1 * x1 * x2,实现方式是和特征缩放一样的,根据一定的规则讲原数据集处理下就好了,然后和多变量线性回归是一样的。根据场景不同也可以将x1的2次方或3次方当做新的特征量,或者x1的平方*x2的3次方等等。。。。花式搭配。