今天去智联招聘面试他们数据分析师的时候,部门boss给我出了三道题,前两道暂且不提,第三道很有意思,作文以记之。
题目3:1楼到10楼的每层电梯门口都放着一颗钻石,钻石大小不一(各不相同)。你乘坐电梯从1楼到10楼,每层楼电梯门都会打开一次,只能拿一次钻石且没有掉头向下的机会,问怎样才能拿到「最大」的一颗?
读完题目我第一反应是动态规划问题,之前记得碰到过类似的扔鸡蛋求临界楼层问题,但仔细一看题目,应该是毫不相关,而且这道题看上去是“无解的”。
我当时不确定问题,就问boss这道题看似无法保证最优解,boss笑着告诉我说你告诉我你思路即可,并给我限制了7分钟的解题时间。
我给出了思路,大致如下:
1.肯定不会在一开始就伸手拿钻石,因为最大那颗钻石放在一楼概率是0.1
2.二楼该不该拿?因为二楼有两种可能,钻石比1楼大,也可能比1楼小,同样的最大那颗钻石放在2楼概率也为0.1,但是有了1楼钻石做参照,2楼钻石较大时去拿,显然获取到最大的那颗钻石的概率更大,但是最大的钻石出现在1楼或2楼的概率为0.2,还是太低,不取。
3.根据以上思路,应该会有某个楼层k,我们将k楼层之前的楼层做为训练集,k楼层做为支持向量,凡是在k层之后出现的比之前所有钻石都大的那颗我们就拿下。这样应该能保证取到最大的那颗钻石的概率最大。
时间比较短,想法也很简陋,并未深究,好在部门boss对我的思路表示还算满意,并提示我回去查看37%法则,告诉我有严格数学证明。
====================================================================
根据此题我也专门查看了37%法则,依据法则解题如下
====================================================================
之前思路其实是37%法则的朴素来源,这里假设有n个楼层,n可以趋向于无穷大。
对于某个固定楼层k,如果所有钻石中最大的那颗钻石出现在了第 i 个位置(k < i ≤ n),要想让它正好被我们选中,就必须得满足前 i-1 个钻石中的最大的钻石在前 k 层里面,这有 k/(i-1) 的可能。考虑所有可能的 i,我们便得到了试探前 k 层之后能选中最大钻石的总概率 P(k):
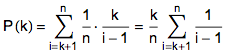 【1】
【1】
用 x 来表示 k/n ,(假设 n 充分大),则公式1可以写成如下变限积分形式:
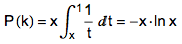 【2】
【2】
对P(k)求导,令其为0(求极大值,x的区间为(0,1)),解得k=n/e
也就是说,在我们这道题目中应该在k=10/e≈3.678=4层
也就是说,我们在4层过后取第一颗出现的,比之前4层都要大的钻石即可保证1/e的概率(约为37%)拿到最大的那颗钻石。
假如没有出现这样的钻石,我们取第十层的那颗即可。
这其实就是机器学习领域常用到的最大似然估计,没事的时候还要多翻翻书才是。