JavaScript 精度问题以及JavaScript 浮点数陷阱及解决方案

阅读完本文可以了解到 0.1 + 0.2 为什么等于 0.30000000000000004 以及 JavaScript 中最大安全数是如何来的。

十进制小数转为二进制小数方法

拿 173.8125 举例如何将之转化为二进制小数。

①. 针对整数部分 173，采取除 2 取余，逆序排列;

173 / 2 = 86 ... 1
86 / 2 = 43 ... 0
43 / 2 = 21 ... 1   ↑
21 / 2 = 10 ... 1   | 逆序排列
10 / 2 = 5 ... 0    |
5 / 2 = 2 ... 1     |
2 / 2 = 1 ... 0
1 / 2 = 0 ... 1

得整数部分的二进制为 10101101。

②. 针对小数部分 0.8125，采用乘 2 取整，顺序排列;

0.8125 * 2 = 1.625  |
0.625 * 2 = 1.25    | 顺序排列
0.25 * 2 = 0.5      |
0.5 * 2 = 1         ↓

得小数部分的二进制为 1101。

③. 将前面两部的结果相加，结果为 10101101.1101;

小心，二进制小数丢失了精度！

根据上面的知识，将十进制小数 0.1 转为二进制：

0.1 * 2 = 0.2
0.2 * 2 = 0.4 // 注意这里
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
0.2 * 2 = 0.4 // 注意这里，循环开始
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
...

可以发现有限十进制小数 0.1 却转化成了无限二进制小数 0.00011001100...，可以看到精度在转化过程中丢失了！

能被转化为有限二进制小数的十进制小数的最后一位必然以 5 结尾(因为只有 0.5 * 2 才能变为整数)。所以十进制中一位小数 0.1 ~ 0.9 当中除了 0.5 之外的值在转化成二进制的过程中都丢失了精度。

推导 0.1 + 0.2 为何等于 0.30000000000000004

在 JavaScript 中所有数值都以 IEEE-754 标准的 64 bit 双精度浮点数进行存储的。先来了解下 IEEE-754 标准下的双精度浮点数。

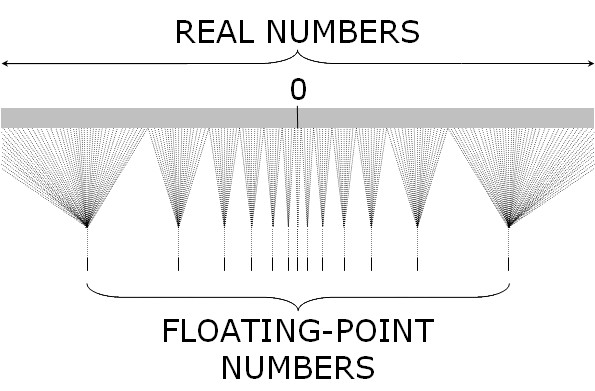
这幅图很关键，可以从图中看到 IEEE-754 标准下双精度浮点数由三部分组成，分别如下：

• sign(符号): 占 1 bit, 表示正负;
• exponent(指数): 占 11 bit，表示范围;
• mantissa(尾数): 占 52 bit，表示精度，多出的末尾如果是 1 需要进位;

　　

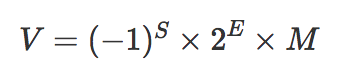
注意以上的公式遵循科学计数法的规范，在十进制是为0<M<10，到二进行就是0<M<2。也就是说整数部分只能是1，所以可以被舍去，只保留后面的小数部分。如 4.5 转换成二进制就是 100.1，科学计数法表示是 1.001*2^2，舍去1后 M = 001。E是一个无符号整数，因为长度是11位，取值范围是 0~2047。但是科学计数法中的指数是可以为负数的，所以再减去一个中间数 1023，[0,1022]表示为负，[1024,2047] 表示为正。如4.5 的指数E = 1025，尾数M为 001。

最终的公式变成：

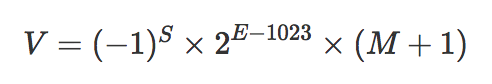
 所以 4.5 最终表示为（M=001、E=1025）：

下面再以 0.1 例解释浮点误差的原因， 0.1 转成二进制表示为 0.0001100110011001100(1100循环)，1.100110011001100x2^-4，所以 E=-4+1023=1019；M 舍去首位的1，得到 100110011...。最终就是：

 转化成十进制后为 0.100000000000000005551115123126，因此就出现了浮点误差。

精度位总共是 53 bit，因为用科学计数法表示，所以首位固定的 1 就没有占用空间。即公式中 (M + 1) 里的 1。另外公式里的 1023 是 2^11 的一半。小于 1023 的用来表示小数，大于 1023 的用来表示整数。

指数可以控制到 2^1024 - 1，而精度最大只达到 2^53 - 1，两者相比可以得出 JavaScript 实际可以精确表示的数字其实很少。

0.1 转化为二进制为 0.0001100110011...，用科学计数法表示为 1.100110011... x 2^(-4)，根据上述公式，S 为 0(1 bit)，E 为 -4 + 1023，对应的二进制为 01111111011(11 bit)，M 为 1001100110011001100110011001100110011001100110011010(52 bit，另外注意末尾的进位)，0.1 的存储示意图如下:

同理，0.2 转化为二进制为 0.001100110011...，用科学计数法表示为 1.100110011... x 2^(-3)，根据上述公式，E 为 -3 + 1023，对应的二进制为 01111111100, M 为 1001100110011001100110011001100110011001100110011010, 0.2 的存储示意图如下:

0.1 + 0.2 即 2^(-4) x 1.1001100110011001100110011001100110011001100110011010 与 2^(-3) x 1.1001100110011001100110011001100110011001100110011010 之和

// 计算过程
0.00011001100110011001100110011001100110011001100110011010
0.0011001100110011001100110011001100110011001100110011010

// 相加得
0.01001100110011001100110011001100110011001100110011001110

0.01001100110011001100110011001100110011001100110011001110 转化为十进制就是 0.30000000000000004。验证完成!

JavaScript 的最大安全数是如何来的

根据双精度浮点数的构成，精度位数是 53 bit。安全数的意思是在 -2^53 ~ 2^53 内的整数(不包括边界)与唯一的双精度浮点数互相对应。举个例子比较好理解：

Math.pow(2, 53) === Math.pow(2, 53) + 1 // true

Math.pow(2, 53) 竟然与 Math.pow(2, 53) + 1 相等！这是因为 Math.pow(2, 53) + 1 已经超过了尾数的精度限制(53 bit)，在这个例子中 Math.pow(2, 53) 和 Math.pow(2, 53) + 1 对应了同一个双精度浮点数。所以 Math.pow(2, 53) 就不是安全数了。

最大的安全数为 Math.pow(2, 53) - 1，即 9007199254740991。

业务中碰到的精度问题以及解决方案

了解 JavaScript 精度问题对我们业务有什么帮助呢？举个业务场景：比如有个订单号后端 Java 同学定义的是 long 类型，但是当这个订单号转换成 JavaScript 的 Number 类型时候精度会丢失了，那没有以上知识铺垫那就理解不了精度为什么会丢失。

为什么 0.1+0.2=0.30000000000000004？

计算步骤为：

// 0.1 和 0.2 都转化成二进制后再进行运算
0.00011001100110011001100110011001100110011001100110011010 +
0.0011001100110011001100110011001100110011001100110011010 =
0.0100110011001100110011001100110011001100110011001100111

// 转成十进制正好是 0.30000000000000004

为什么 x=0.1 能得到 0.1？

恭喜你到了看山不是山的境界。因为 mantissa 固定长度是 52 位，再加上省略的一位，最多可以表示的数是 2^53=9007199254740992，对应科学计数尾数是 9.007199254740992，这也是 JS 最多能表示的精度。它的长度是 16，所以可以使用 toPrecision(16) 来做精度运算，超过的精度会自动做凑整处理。于是就有：

0.10000000000000000555.toPrecision(16)
// 返回 0.1000000000000000，去掉末尾的零后正好为 0.1

// 但你看到的 `0.1` 实际上并不是 `0.1`。不信你可用更高的精度试试：
0.1.toPrecision(21) = 0.100000000000000005551

大数危机

可能你已经隐约感觉到了，如果整数大于 9007199254740992 会出现什么情况呢？
由于 E 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1，这就是能表示的最大整数。但你并不能这样计算这个数字，因为从 2^1024 开始就变成了 Infinity

> Math.pow(2, 1023)
8.98846567431158e+307

> Math.pow(2, 1024)
Infinity

那么对于 (2^53, 2^63) 之间的数会出现什么情况呢？

• (2^53, 2^54) 之间的数会两个选一个，只能精确表示偶数
• (2^54, 2^55) 之间的数会四个选一个，只能精确表示4个倍数
• ... 依次跳过更多2的倍数

下面这张图能很好的表示 JavaScript 中浮点数和实数（Real Number）之间的对应关系。我们常用的 (-2^53, 2^53) 只是最中间非常小的一部分，越往两边越稀疏越不精确。

在淘宝早期的订单系统中把订单号当作数字处理，后来随意订单号暴增，已经超过了
9007199254740992，最终的解法是把订单号改成字符串处理。

要想解决大数的问题你可以引用第三方库 bignumber.js，原理是把所有数字当作字符串，重新实现了计算逻辑，缺点是性能比原生的差很多。所以原生支持大数就很有必要了，现在 TC39 已经有一个 Stage 3 的提案 proposal bigint，大数问题有望彻底解决。在浏览器正式支持前，可以使用 Babel 7.0 来实现，它的内部是自动转换成 big-integer 来计算，要注意的是这样能保持精度但运算效率会降低。

toPrecision vs toFixed

数据处理时，这两个函数很容易混淆。它们的共同点是把数字转成字符串供展示使用。注意在计算的中间过程不要使用，只用于最终结果。

不同点就需要注意一下：

• toPrecision 是处理精度，精度是从左至右第一个不为0的数开始数起。
• toFixed 是小数点后指定位数取整，从小数点开始数起。

两者都能对多余数字做凑整处理，也有些人用 toFixed 来做四舍五入，但一定要知道它是有 Bug 的。

如：1.005.toFixed(2) 返回的是 1.00 而不是 1.01。

原因： 1.005 实际对应的数字是 1.00499999999999989，在四舍五入时全部被舍去！

解法：使用专业的四舍五入函数 Math.round() 来处理。但 Math.round(1.005 * 100) / 100 还是不行，因为 1.005 * 100 = 100.49999999999999。还需要把乘法和除法精度误差都解决后再使用 Math.round。可以使用后面介绍的 number-precision#round 方法来解决。

解决方案

回到最关心的问题：如何解决浮点误差。首先，理论上用有限的空间来存储无限的小数是不可能保证精确的，但我们可以处理一下得到我们期望的结果。

数据展示类

当你拿到 1.4000000000000001 这样的数据要展示时，建议使用 toPrecision 凑整并 parseFloat 转成数字后再显示，如下：

parseFloat(1.4000000000000001.toPrecision(12)) === 1.4  // True

封装成方法就是：

//字符串转换成数字并处理精度问题
function parseNums(ratio) {
　　if(ratio===null)return "";
　　if(ratio==="")return "";
　　return parseFloat((ratio*100).toPrecision(12));
}

为什么选择 12 做为默认精度？这是一个经验的选择，一般选12就能解决掉大部分0001和0009问题，而且大部分情况下也够用了，如果你需要更精确可以调高。

数据运算类

对于运算类操作，如 +-*/，就不能使用 toPrecision 了。正确的做法是把小数转成整数后再运算。以加法为例：

/**
 * 精确加法
 */
function add(num1, num2) {
  const num1Digits = (num1.toString().split('.')[1] || '').length;
  const num2Digits = (num2.toString().split('.')[1] || '').length;
  const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));
  return (num1 * baseNum + num2 * baseNum) / baseNum;
}

以上方法能适用于大部分场景。遇到科学计数法如 2.3e+1（当数字精度大于21时，数字会强制转为科学计数法形式显示）时还需要特别处理一下。