索引原理
B+树索引
查找一个特定值这个树挺好用,但是当你需要查找两个值之间的多个元素时,就会有大麻烦了。你的成本将是 O(N),所以引用一种B+树的结构
如图
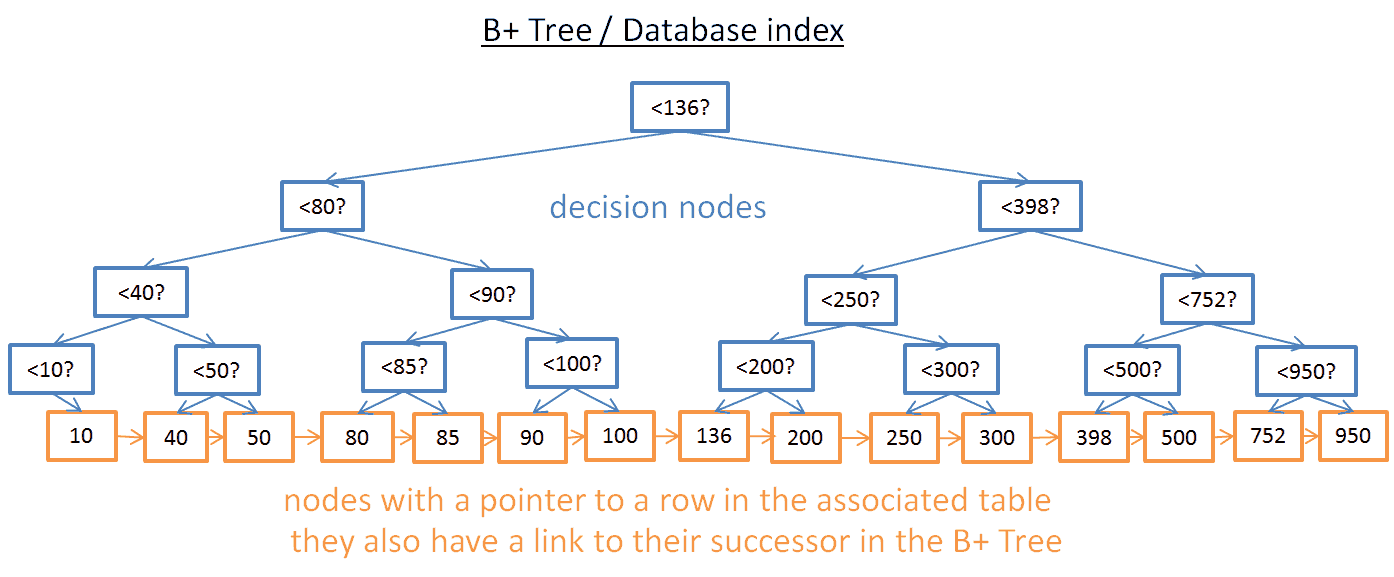
比方说你找到了 M 个后续节点,树总共有 N 个节点。对指定节点的搜索成本是 log(N),跟上一个树相同。但是当你找到这个节点,你得通过后续节点的连接得到 M 个后续节点,这需要 M 次运算。那么这次搜索只消耗了 M+log(N) 次运算,区别于上一个树所用的 N 次运算。此外,你不需要读取整个树(仅需要读 M+log(N) 个节点),这意味着更少的磁盘访问。如果 M 很小(比如 200 行)并且 N 很大(1,000,000),那结果就是天壤之别了
但是有个问题,树的平衡是需要成本的。
在B+树中,插入和删除操作是 O(log(N)) 复杂度。另外索引的增加对于事物管理器也会有负担
这样,就需要引入另一种索引机制
Hash索引
如果数据都存储在同一个数据库块上,并且将HASH索引作为WHERE子句中的确切匹配,Oracle就可以通过执行一个HASH函数和I/O来访问数据,如图:
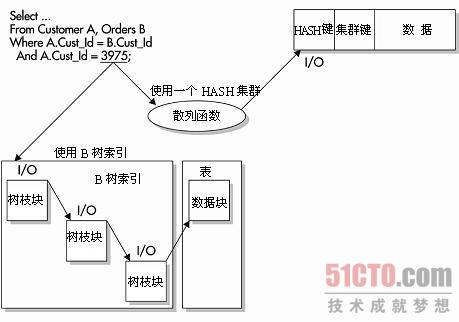
HASH索引可能是访问数据库中数据的最快方法,但它也有自身的缺点
它们只适对等比较,如:= > < ,不适合用于范围查询,同时大规模的Hash带来的Hash冲突也会造成性能的下降。
另外Hash需要在集群上,由于集群存在增长的问题,为Hash索引分配空间也是一个问题