支持向量机（Support Vector Machine / SVM）

支持向量机(Support Vector Machines, SVM)：是一种机器学习算法。

支持向量(Support Vector)就是离分隔超平面最近的那些点。
机(Machine)就是表示一种算法，而不是表示机器。

基于训练集样本在空间中找到一个划分超平面，将不同类别的样本分开。

SVM 工作原理

找到距离距离最近的炸弹，距离它们最远。

1. 寻找最大的分类间距；

2. 转为通过拉格朗日函数求优化的问题。  

 找到离分隔超平面最近的点，确保它们离分隔面的的距离尽可能远。

怎么寻找最大间隔？

点到超平面的距离

• 分隔超平面函数间距: (y(x)=w^Tx+b)
• 分类的结果： (f(x)=sign(w^Tx+b)) (sign表示>0为1，<0为-1，=0为0)
• 点到超平面的几何间距: (d(x)=(w^Tx+b)/||w||) （||w||表示w矩阵的二范式=> (sqrt{w*w^T}), 点到超平面的距离也是类似的）

 

拉格朗日乘子法

类别标签用-1、1，是为了后期方便 (lable(w^Tx+b)) 的标识和距离计算；如果 (lable(w^Tx+b)>0) 表示预测正确，否则预测错误。

现在目标很明确，就是要找到w和b，因此我们必须要找到最小间隔的数据点，也就是前面所说的支持向量。

也就说，让最小的距离取最大.(最小的距离：就是最小间隔的数据点；最大：就是最大间距，为了找出最优超平面--最终就是支持向量)
目标函数：(arg: max_{关于w, b} left( min[lable(w^Tx+b)]frac{1}{||w||} ight) )
如果 (lable*(w^Tx+b)>0) 表示预测正确，也称函数间隔，(||w||) 可以理解为归一化，也称几何间隔。
令 (lable(w^Tx+b)>=1)， 因为0～1之间，得到的点是存在误判的可能性，所以要保障 (min[lable(w^Tx+b)]=1)，才能更好降低噪音数据影响。
所以本质上是求 (arg: max_{关于w, b} frac{1}{||w||} )；也就说，我们约束(前提)条件是: (lable*(w^Tx+b)=1)
新的目标函数求解： (arg: max_{关于w, b} frac{1}{||w||} )

=> 就是求: (arg: min_{关于w, b} ||w|| ) (求矩阵会比较麻烦，如果x只是 (frac{1}{2}*x^2) 的偏导数，那么。。同样是求最小值)
=> 就是求: (arg: min_{关于w, b} (frac{1}{2}*||w||^2)) (二次函数求导，求极值，平方也方便计算)
本质上就是求线性不等式的二次优化问题(求分隔超平面，等价于求解相应的凸二次规划问题)
通过拉格朗日乘子法，求二次优化问题

假设需要求极值的目标函数 (objective function) 为 f(x,y)，限制条件为 φ(x,y)=M # M=1
设g(x,y)=M-φ(x,y) # 临时φ(x,y)表示下文中 (label*(w^Tx+b))
定义一个新函数: F(x,y,λ)=f(x,y)+λg(x,y)
a为λ（a>=0），代表要引入的拉格朗日乘子(Lagrange multiplier)
那么： (L(w,b,alpha)=frac{1}{2} * ||w||^2 + sum_{i=1}^{n} alpha_i * [1 - label * (w^Tx+b)])
因为：(label(w^Tx+b)>=1, alpha>=0) , 所以 (alpha[1-label(w^Tx+b)]<=0) , (sum_{i=1}^{n} alpha_i * [1-label(w^Tx+b)]<=0)
相当于求解： (max_{关于alpha} L(w,b,alpha) = frac{1}{2} *||w||^2)
如果求： (min_{关于w, b} frac{1}{2} *||w||^2) , 也就是要求： (min_{关于w, b} left( max_{关于alpha} L(w,b,alpha) ight))
现在转化到对偶问题的求解

(min_{关于w, b} left(max_{关于alpha} L(w,b,alpha) ight) ) >= (max_{关于alpha} left(min_{关于w, b} L(w,b,alpha) ight) )
现在分2步
先求： (min_{关于w, b} L(w,b,alpha)=frac{1}{2} * ||w||^2 + sum_{i=1}^{n} alpha_i * [1 - label * (w^Tx+b)])
就是求L(w,b,a)关于[w, b]的偏导数, 得到w和b的值，并化简为：L和a的方程。

• 

  

  f(wTx+b),其中u<0时f(u)输出-1,反之则输出+1

  点到超平面的几何间距: (d(x)=(w^Tx+b)/||w||) （||w||表示w矩阵的二范式=> (sqrt{w*w^T}),

  现在的目标就是找出分类器定义中的w和b，我们必须找到具有最小间隔的数据点，而 这些数据点也就是前面提到的支持向量。一旦找到具有最小间隔的数据点，我们就需要对该间隔 最大化。

  

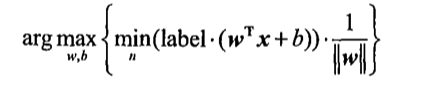
  通过引人拉格朗日乘子，我们就可以基于约束条件来表述原来的问 题。由于这里的约束条件都是基于数据点的，因此我们就可以将超平面写成数据点的形式。于是, 优化目标函数最后可以写成:

  

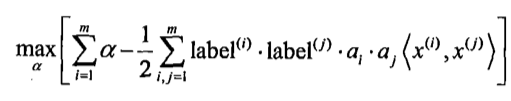
  约束条件：

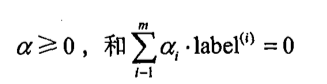
  松弛变量(slack variable)

  
  我们知道几乎所有的数据都不那么干净, 通过引入松弛变量来允许数据点可以处于分隔面错误的一侧。
  约束条件： (C>=a>=0) 并且 (sum_{i=1}^{m} a_i·label_i=0)
  这里常量C用于控制“最大化间隔”和“保证大部分点的函数间隔小于1.0” 这两个目标的权重。
  常量C是一个常数，我们通过调节该参数得到不同的结果。一旦求出了所有的alpha，那么分隔超平面就可以通过这些alpha来表示。
  这一结论十分直接，SVM中的主要工作就是要求解 alpha.

  通过引人所谓松弛变来允 许有些数据点可以处于分隔面的错误一侧。这样我们的优化目标就能保持仍然不变，但是此时新 的约束条件则变为:

   

  常熟C就是用于控制“最大化间隔”和“保证大部分点的函数间隔小于1.0”这两个目标的权重。、

  常熟C是一个参数，通过调参得到不同的结果。

  求出所有的alpha，分隔平面就能通过这些alpha来表达。

  SVM的主要工作就是求解这些alpha。

  SVM有很多种实现，最流行的一种实现是： 序列最小优化(Sequential Minimal Optimization, SMO)算法。

  SMO 伪代码大致如下：

  • SMO用途：用于训练 SVM
  • SMO目标：求出一系列 alpha 和 b,一旦求出 alpha，就很容易计算出权重向量 w 并得到分隔超平面。
  • SMO思想：是将大优化问题分解为多个小优化问题来求解的。
  • SMO原理：每次循环选择两个 alpha 进行优化处理，一旦找出一对合适的 alpha，那么就增大一个同时减少一个。
    • 这里指的合适必须要符合一定的条件
      1. 这两个 alpha 必须要在间隔边界之外
      2. 这两个 alpha 还没有进行过区间化处理或者不在边界上。
    • 之所以要同时改变2个 alpha；原因是我们有一个约束条件： (sum_{i=1}^{m} a_i·label_i=0)；如果只是修改一个 alpha，很可能导致约束条件失效。

  建一个 alpha 向量并将其初始化为0向量
  当迭代次数小于最大迭代次数时(外循环)
      对数据集中的每个数据向量(内循环)：
          如果该数据向量可以被优化
              随机选择另外一个数据向量
              同时优化这两个向量
              如果两个向量都不能被优化，退出内循环
      如果所有向量都没被优化，增加迭代数目，继续下一次循环
  

  核函数(kernel) 使用

  • 对于线性可分的情况，效果明显
  • 对于非线性的情况也一样，此时需要用到一种叫核函数(kernel)的工具将数据转化为分类器易于理解的形式。

  可以将数据从某个特征空间到另一个特征空间的映射。（通常情况下：这种映射会将低维特征空间映射到高维空间。）

  经过空间转换后：低维需要解决的非线性问题，就变成了高维需要解决的线性问题。

  SVM 优化特别好的地方，在于所有的运算都可以写成内积(inner product: 是指2个向量相乘，得到单个标量 或者 数值)；内积替换成核函数的方式被称为核技巧(kernel trick)或者核"变电"(kernel substation)

  核函数并不仅仅应用于支持向量机，很多其他的机器学习算法也都用到核函数。最流行的核函数：径向基函数(radial basis function)

  径向基函数的高斯版本，其具体的公式为：