hdu1710 Binary Tree Traversals(二叉树的遍历)

A binary tree is a finite set of vertices that is either empty or consists of a root r and two disjoint binary trees called the left and right subtrees. There are three most important ways in which the vertices of a binary tree can be systematically traversed or ordered. They are preorder, inorder and postorder. Let T be a binary tree with root r and subtrees T1,T2.

In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.

In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.

In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.

Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.

 

Input

The input contains several test cases. The first line of each test case contains a single integer n (1<=n<=1000), the number of vertices of the binary tree. Followed by two lines, respectively indicating the preorder sequence and inorder sequence. You can assume they are always correspond to a exclusive binary tree.

 

Output

For each test case print a single line specifying the corresponding postorder sequence.

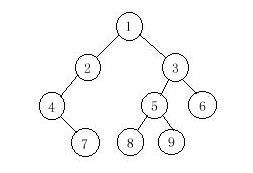
Sample Input

9

1 2 4 7 3 5 8 9 6

4 7 2 1 8 5 9 3 6

 

Sample Output

7 4 2 8 9 5 6 3 1

//根据前序和中序遍历写出后序遍历
#include<iostream>
using namespace std;
int t1[1001],t2[1001];
void sousuo(int a,int b,int n,int flag)
{
    
    if(n==1)//如果存在左子树或右子树就直接输出
    {
        printf("%d ",t1[a]);
        return ;
    }
    else if(n<=0)//如果不存在左子树或右子树就返回上一层
        return ;
    int i;//继续罚分为左子树和右子树
    for(i=0;t1[a]!=t2[b+i];i++) ;//找到罚分点也就是根节点
    sousuo(a+1,b,i,0);//左子树的遍历
    sousuo(a+i+1,b+i+1,n-i-1,0);//右子树的遍历
    if(flag==1)//最原始的跟节点
        printf("%d",t1[a]);
    else//一般的根节点
        printf("%d ",t1[a]);
}
int main()
{
    int n,i;
    while(scanf("%d",&n)!=EOF)
    {
        for(i=1;i<=n;i++)
            scanf("%d",&t1[i]);//t1中存的是前序
        for(i=1;i<=n;i++)//t2中存的中序
            scanf("%d",&t2[i]);
        sousuo(1,1,n,1);
        printf("
");
    }
    return 0;
}