zoukankan html css js c++ java

java-实现平衡二叉树

1，前面一条博客实现了，二叉查找树，但是当二叉树退化成链表后，二叉查找树的时间复杂度优越性就没有了，

再网上学习了一下，啊啊啊，调了一夜bug，5555

主要参考博主的博客：https://www.cnblogs.com/qm-article/p/9349681.html

实现平衡二叉树是基于，二叉查找树的，所以建议先写一遍二叉查找树，再学二叉平衡操作原理，把自己的二叉查找树变成，平衡二叉树。（可以一步一步，先实现添加节点-添加完就是一颗排序树，中序遍历就是排序序列，再实现删除功能，就完成了二叉查找树，再实现平衡功能就是平衡二叉树）
我自己的二叉查找树：上一篇博客，参考了博主的文章后，将Node节点新增了一个指向父节点的指针，这样不用特地去表记preNode,也便于回溯平衡操作，因为先将子树平衡，母树才能平衡。但是增加了一个指针（java里其实是引用，一个意思，只不过用对象代替了），再添加节点和删除节点的时候的指针指向要特别注意，调式bug 也主要在这里，如果父指针没有修改，回溯的时候不知道会回溯到哪
平衡二叉树的核心还是平衡操作，学习：https://www.cnblogs.com/qm-article/p/9349681.html，博主分析的还是挺清晰的，我在bb一遍，加深一下我自己的印象，233

网上搜的在线动态生存二叉树、平衡二叉树的网站：https://visualgo.net/zh/bst

2 原理：

2.1当平衡的树节点变动后（添加删除操作），变得非平衡了，因为平衡状态根节点左右子树高度差为-1、0、1。所以可以枚举一下添加节点失衡前的状态高度差为1（-1与之对称）：即再添加就会失衡，这三种是节点高度差为2（-2的对称一下），即需要右旋才能平衡的状态。

----父节点或者null(A为根节点)

2.2，枚举失衡状态

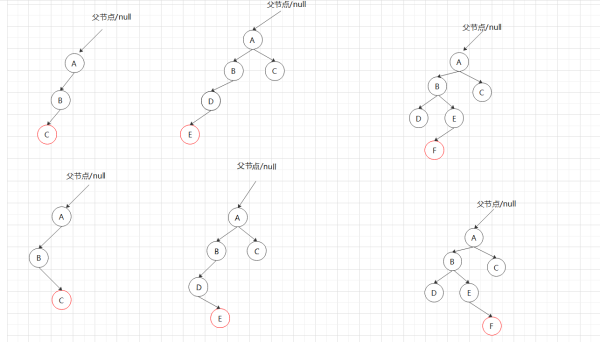
左边4状态其实等于左边两种，中间的两种，不看A节点的话，就是左边两种状态，

①关于左上状态，A节点高度差为2，直接右旋即可，B.father=A.father;B.right=A,A.father=B;A.right=B.left(null);

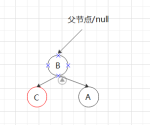
②左下的状态，A的高度差为2，但不能直接右旋，先以B为根节点将子树左旋为后，再进行如左上①右旋

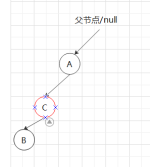
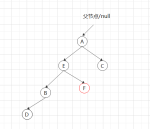
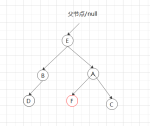
③右下，如果直接右旋如图：

要先以B为根左旋，以A为根右旋

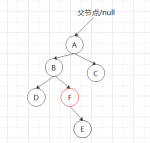
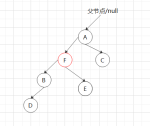
④右上，产生高度差的节点是A,如果直接右旋会如图：

等于没旋，还是不平衡，要先以B节点为根左旋，B为根节点左旋又牵扯到左下②的情况，先右旋再左旋，再以A为节点右旋

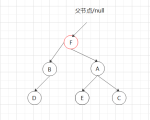
总结一下就是：触发高度差=2/-2的节点（要右/左旋）nodeA，其左子节点nodeB,若nodeB无子节点，则直接右/左旋，若有子节点，先以nodeB为根节点左/右旋，再以nodeA为根节点右/左旋

右旋代码：

 1 public Node rightRotation(Node nodeA){
 2     if(nodeA==null)
 3         return null;
 4     else{
 5         Node nodeB=nodeA.lchild;
 6         nodeA.lchild=nodeB.rchild;
 7         if(nodeB.rchild!=null)
 8             nodeB.rchild.father=nodeA;
 9         nodeB.rchild=nodeA;
10         nodeB.father=nodeA.father;
11         if(nodeA.father==null)
12             this.root=nodeB;
13         else{
14             if(nodeA.father.lchild==nodeA)
15                 nodeA.father.lchild=nodeB;
16             else
17                 nodeA.father.rchild=nodeB;
18         }
19         nodeA.father=nodeB;
20         return nodeB;
21     }
22 }

View Code

2.3左旋的情况相反，与左旋对称，

左旋代码：

 1 public Node leftRotation(Node nodeA){
 2         if(nodeA==null)
 3             return null;
 4         else{
 5             Node nodeB=nodeA.rchild;
 6             nodeA.rchild=nodeB.lchild;
 7             if(nodeB.lchild!=null)
 8                 nodeB.lchild.father=nodeA;
 9             nodeB.lchild=nodeA;
10             nodeB.father=nodeA.father;
11             if(nodeA.father==null)
12                 this.root=nodeB;
13             else{
14                 if(nodeA.father.lchild==nodeA)
15                     nodeA.father.lchild=nodeB;
16                 else
17                     nodeA.father.rchild=nodeB;
18             }
19             nodeA.father=nodeB;
20             return nodeB;
21         }
22     }

View Code

判断----执行哪种旋转操作，左 / 右 / 左右 / 右左

 1 /**
 2      * 求高度差，函数
 3      */
 4     public int heightDifference(Node root){
 5         return treeHeightRec(root.lchild)-treeHeightRec(root.rchild);
 6     }
 7 
 8     //调用平衡
 9 
10 public void banlanceTree(Node p){
11         while(p!=null){
12             //右旋
13             if(heightDifference(p)==2){
14                 Node nodeB=p.lchild;
15                 //如果b有右子节点，先将b左旋，再将a右旋
16                 if(nodeB.rchild!=null){
17                     leftRotation(nodeB);
18                     rightRotation(p);
19                 }
20                 //如果b无右子节点，将a右旋
21                 else
22                     rightRotation(p);
23             }
24             //左旋
25             else if(heightDifference(p)==-2){
26                 Node nodeB=p.rchild;
27                 //如果b有左子节点，先将b右旋，再将a左旋
28                 if(nodeB.lchild!=null){
29                     rightRotation(nodeB);
30                     leftRotation(p);
31                 }
32                 //如果b无左子节点，a左旋
33                 else
34                     leftRotation(p);
35             }
36             p=p.father;
37         }
38     }

View Code

平衡函数在每一次变动树元素之后调用----添加函数，删除函数，删除最大值，删除最小值。

2.4，说一下删除的时候一些情况，

我刚开始看博客的时候有一个误区，一直纠结了很久，最后是因为看的不仔细，没注意（nodeB只要有子节点，就要先左/右旋，再右/左旋）我原本分了三种情况，①AB均无子节点，直接旋转，

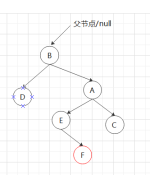
②A无右子节点，B有（就是枚举图对于左下的图），要先反旋，再旋，③（我把剩下的都放在这里了）A有右子节点，B也有，就直接旋，把B的子节点给A,直到后来调试删除函数的时候遇到一种情况：

F是待删节点，删掉后回溯到C,高度差为0，继续回溯到A,高度差为2，AB都有右子节点，右旋，交接子节点（子树）。

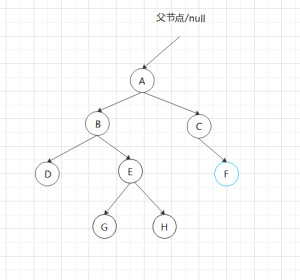
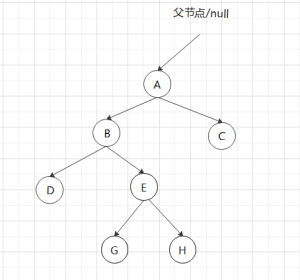
然后发现，旋来旋去都没用了，回去看博客才发现自己看的太草率了。

正解是，删除F后，向上回溯，C高度差为0，继续，到A,高度差为2要右旋（右旋还分直接旋和间接旋），因为B有右子树，所以触发以B为根节点的左旋即：

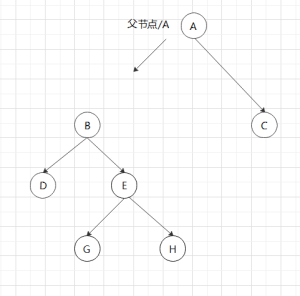
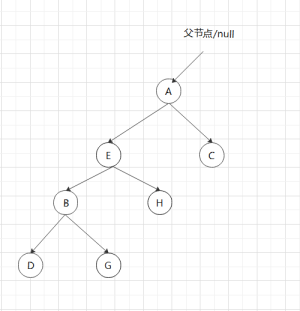
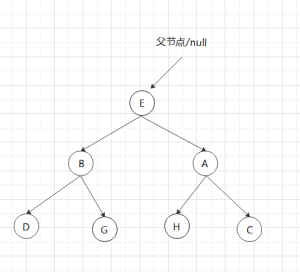
完整代码，

  1 /**
  2  * 二叉查找树，在某些情况下二叉树退化成链表，时间复杂度上升，平衡二叉树就是解决这一问题的
  3  * 建树过程中，没插入一个节点都对树进行平衡
  4  *
  5  * 转载：https://www.cnblogs.com/qm-article/p/9349681.html
  6  * 借鉴了。Node 添加一个父节点操作
  7  */
  8 
  9 /**
 10  * 这里有一个bug，就是删除函数里面引用了，删除最大值/最小值函数并且这两个函数有返回值，
 11  * 再处理被删节点有左/右子树，取右子树最小值代替被删节点上很方便，但是如果单独使用删除大值
 12  * 最小值函数，就无法调用平衡操作，牵扯到，返回值，无法从被删除的节点精准的回溯，这也不只是
 13  * 减少时间的问题，只能反向回溯，如果正向遍历，根节点的高度差，受子树根节点高度差影响，只能先解决子树
 14  * 的平衡问题
 15  *
 16  * 解决方案：直接复制两个删除最大值，/最小值函数换个函数名，专供删除值调用，原删除最大值/最小值函数不用返回值，
 17  *                                                                  （不行，对象还是可以调用这4 个函数）
 18  * ②直接将函数写进delete里面
 19  *写进去太delete函数太长了，这bug 不象处理了，233，--搞吧，写完以后应该也不会再弄了，调式的很烦啊，啊啊啊啊
 20  *
 21  */
 22 
 23 
 24 import java.util.LinkedList;
 25 import java.util.Queue;
 26 public class AVLTree {
 27 
 28     public class Node{
 29         private Node father=null;
 30         private Node lchild=null;
 31         private Node rchild=null;
 32 
 33         private int data=Integer.MAX_VALUE;
 34 
 35         public Node(){}
 36         public Node(int data){
 37             this.data=data;
 38         }
 39     }
 40 
 41 
 42     private Node root=null;
 43 
 44     /**
 45      * 复制上一篇，主要是插入时，添加父节点指针，添加完成，平衡
 46      */
 47     //是否存在
 48     public boolean isExist(Node root,int data){
 49         if(root==null)//树空
 50             return false;
 51         if(root.data==data)
 52             return true;
 53         else if(data<root.data){
 54             if(root.lchild==null)
 55                 return false;
 56             else
 57                 return isExist(root.lchild,data);
 58         }else{
 59             if(root.rchild==null)
 60                 return false;
 61             else
 62                 return isExist(root.rchild,data);
 63         }
 64     }
 65     //插入-建树
 66     public void inseart(Node root,int data){
 67         if(isExist(root,data)){
 68             System.out.println(data+"已经存在树中");
 69             return;
 70         }
 71         //树空插入根节点--不用回溯，直接return
 72         if(root==null){
 73             this.root=new Node(data);
 74             return;
 75         }
 76         else{
 77             //元素不能重复，
 78             if(data<root.data){
 79                 if(root.lchild==null){
 80                     Node newNode=new Node(data);
 81                     root.lchild=newNode;
 82                     newNode.father=root;
 83                 }
 84                 else{
 85                     inseart(root.lchild,data);
 86                 }
 87             }
 88             else{
 89                 if(root.rchild==null){
 90                     Node newNode=new Node(data);
 91                     root.rchild=newNode;
 92                     newNode.father=root;
 93                 }else
 94                     inseart(root.rchild,data);
 95             }
 96         }
 97         //插入完了要回溯，平衡
 98         banlanceTree(root);
 99     }
100 
101     /**删除-主体复制上一篇，因为新加了，父节点指针，preNode和删除代码那里需要改一下
102      * 先实现删除最大值最小值，
103      *
104      * 删除后-平衡
105      */
106     //修改指针关系
107     public void deleteMin(Node root){
108         //空树
109         if(root==null){
110             System.out.println("树空,无最小值");
111             return;
112         }
113         //只有一个根节点
114         else if(root.lchild==null&&root.rchild==null){
115             this.root=null;
116             return;
117         }
118         //根节点无左子树（删除根节点）
119         else if(root.lchild==null){
120             this.root=root.rchild;
121             root.rchild.father=null;
122         }
123         //有左子树且非空
124         while(root.lchild!=null){
125             root=root.lchild;
126         }
127         root.father.lchild=root.rchild;
128         if(root.rchild!=null)
129             root.rchild.father=root.father;
130 
131         root.rchild=null;
132         banlanceTree(root);
133     }
134     //修改指针关系
135     public void deleteMax(Node root){
136         //空树
137         if(root==null){
138             System.out.println("树空，无最大值");
139             return;
140         }
141         //只有一个根节点
142         else if(root.lchild==null&&root.rchild==null){
143             if(root.father==null)
144                 this.root=null;
145             return;
146         }
147         //根节点无右子树（删除根节点）
148         else if(root.rchild==null){
149             this.root=root.lchild;
150             root.lchild.father=null;
151         }
152         //有右子树且非空
153         else if(root.rchild!=null){
154             while(root.rchild!=null){
155                 root=root.rchild;
156             }
157             root.father.rchild=root.lchild;
158             if(root.lchild!=null)
159                 root.lchild.father=root.father;
160         }
161         root.lchild=null;
162         banlanceTree(root);
163     }
164 
165 
166 
167     public void delete(Node root,int data){
168         //在树中（树非空）
169         if(!isExist(root,data)){
170             System.out.println(data+"值不在树中");
171             return;
172         }
173         //以下默认在树中
174 
175         //只有一个节点-即删除根节点
176         if(root.lchild==null&&root.rchild==null){
177             this.root=null;
178             return;
179         }
180         //先遍历到节点，在删除-将替换节点的值赋给该节点，
181         else{
182             while(root.data!=data){
183                 if(data<root.data){
184                     root=root.lchild;
185                 }
186                 else if(data>root.data){
187                     root=root.rchild;
188                 }
189             }
190             //此时root即待删除节点；
191             //该节点无子节点
192             if(root.lchild==null&&root.rchild==null){
193                 if(root.father.lchild==root){
194                     root.father.lchild=null;
195                 }
196                 else{
197                     root.father.rchild=null;
198                 }
199             }
200             //只有左子节点
201             else if(root.lchild!=null&&root.rchild==null){
202                 //拿到左子树的最大值，
203                 //Node replaceNode=deleteMax(root.lchild);
204                             Node p=root.lchild;
205                             if(p.lchild==null&&p.rchild==null){
206                                 if(p.father.lchild==p)
207                                     p.father.lchild=null;
208                                 else
209                                     p.father.rchild=null;
210                             }
211                             //根节点无右子树（删除根节点）
212                             else if(p.lchild!=null&&p.rchild==null){
213                                     if(p.father.lchild==p){
214                                         p.father.lchild=p.lchild;
215                                         p.lchild.father=p.father;
216                                     }else {
217                                         p.father.rchild=p.lchild;
218                                         p.lchild.father=p.father;
219                                     }
220                             }
221                             //有右子树且非空
222                             else if(p.rchild!=null){
223                                 while(p.rchild!=null){
224                                     p=p.rchild;
225                                 }
226                                 p.father.rchild=p.lchild;
227                                 if(p.lchild!=null)
228                                     p.lchild.father=p.father;
229                             }
230                             p.lchild=null;
231                 root.data=p.data;
232             }
233             //有右子节点
234             else if(root.rchild!=null){
235                 //拿到右子树的最小值
236                 //Node replaceNode=deleteMin(root.rchild);
237                                 Node p=root.rchild;
238                                 if(p.lchild==null&&p.rchild==null){
239                                     if(p.father.lchild==p)
240                                         p.father.lchild=null;
241                                     else
242                                         p.father.rchild=null;
243                                 }
244                                 //根节点无左子树（删除根节点）
245                                 else if(p.lchild==null){
246                                     if(p.father.lchild==p){
247                                         p.father.lchild=p.rchild;
248                                         p.rchild.father=p.father;
249                                     }else {
250                                         p.father.rchild=p.rchild;
251                                         p.rchild.father=p.father;
252                                     }
253                                 }
254                                 //有左子树且非空
255                                 else if(p.lchild!=null){
256                                     while(p.lchild!=null){
257                                         p=p.lchild;
258                                     }
259                                     p.father.lchild=p.rchild;
260                                     if(p.rchild!=null)
261                                         p.rchild.father=p.father;
262                                 }
263 
264 
265                                 p.rchild=null;
266                 root.data=p.data;
267             }
268         }
269         //删除完要回溯，平衡
270         Node p=root.father;
271         //System.out.println("p1 "+p.data);
272         banlanceTree(p);
273     }
274 
275 
276 
277     /**辅助函数-从前一篇复制
278      * 求树高
279      * 打印树
280      */
281     //递归求树高-用于打印树
282     //递归
283     public int treeHeightRec(Node root){
284         if(root==null)
285             return 0;
286         else{
287             int a =treeHeightRec(root.lchild);
288             int b = treeHeightRec(root.rchild);
289             return (a>b)?(a+1):(b+1);
290         }
291     }
292     //打印树--233，复制前一篇的方法，如果树层数很深时，打印的比较别扭
293     public void printTree(Node root){
294         int H=treeHeightRec(root);
295         int h=H;
296         //System.out.println("树高："+H);
297         if(H==0)
298             System.out.println("树空,无打印");
299         else{
300             System.out.println("打印树：");
301             Queue<Node> queue=new LinkedList<>();
302             queue.add(root);
303             int height=1;
304             //记录每层孩子个数
305             int len=1;
306             while(h>0){
307                 int length=0;
308                 String space="";
309                 for(int i=0;i<(((Math.pow(2,H)+1)*3)/(Math.pow(2,height)+1));i++)
310                     space+=" ";
311                 for(int i=0;i<len;i++){
312                     Node curroot=queue.poll();
313                     if(curroot.data==Integer.MAX_VALUE){
314                         System.out.print(space);
315                     }else
316                         System.out.print(space+curroot.data);
317 
318                     if(curroot.lchild!=null){
319                         queue.add(curroot.lchild);
320                     }
321                     else
322                         queue.add(new Node());
323                     length++;
324                     if(curroot.rchild!=null){
325                         queue.add(curroot.rchild);
326                     }
327                     else
328                         queue.add(new Node());
329                     length++;
330                 }
331                 System.out.println();
332                 System.out.println();
333                 len=length;
334                 height++;
335                 h--;
336             }
337             System.out.println();
338         }
339     }
340     //中序遍历
341     public void inOrder(Node root){
342         if(root==null)
343             return;
344         inOrder(root.lchild);
345         System.out.print(root.data+" ");
346         inOrder(root.rchild);
347     }
348 
349 
350     /**
351      * 平衡操作
352      * 参考与https://www.cnblogs.com/qm-article/p/9349681.html
353      *①先判断失衡，及执行那种平衡操作
354      * ②平衡操作。左旋，右旋，先左再右旋，先右旋再左旋
355      *
356      */
357 
358     public Node rightRotation(Node nodeA){
359         if(nodeA==null)
360             return null;
361         else{
362             Node nodeB=nodeA.lchild;
363             nodeA.lchild=nodeB.rchild;
364             if(nodeB.rchild!=null)
365                 nodeB.rchild.father=nodeA;
366             nodeB.rchild=nodeA;
367             nodeB.father=nodeA.father;
368             if(nodeA.father==null)
369                 this.root=nodeB;
370             else{
371                 if(nodeA.father.lchild==nodeA)
372                     nodeA.father.lchild=nodeB;
373                 else
374                     nodeA.father.rchild=nodeB;
375             }
376             nodeA.father=nodeB;
377             return nodeB;
378         }
379     }
380 
381     public Node leftRotation(Node nodeA){
382         if(nodeA==null)
383             return null;
384         else{
385             Node nodeB=nodeA.rchild;
386             nodeA.rchild=nodeB.lchild;
387             if(nodeB.lchild!=null)
388                 nodeB.lchild.father=nodeA;
389             nodeB.lchild=nodeA;
390             nodeB.father=nodeA.father;
391             if(nodeA.father==null)
392                 this.root=nodeB;
393             else{
394                 if(nodeA.father.lchild==nodeA)
395                     nodeA.father.lchild=nodeB;
396                 else
397                     nodeA.father.rchild=nodeB;
398             }
399             nodeA.father=nodeB;
400             return nodeB;
401         }
402     }
403 
404     /**
405      * 求高度差，函数
406      */
407     public int heightDifference(Node root){
408         return treeHeightRec(root.lchild)-treeHeightRec(root.rchild);
409     }
410 
411     //调用平衡
412     public void banlanceTree(Node p){
413         while(p!=null){
414             //右旋
415             if(heightDifference(p)==2){
416                 Node nodeB=p.lchild;
417                 //如果b有右子节点，先将b左旋，再将a右旋
418                 if(nodeB.rchild!=null){
419                     leftRotation(nodeB);
420                     rightRotation(p);
421                 }
422                 //如果b无右子节点，将a右旋
423                 else
424                     rightRotation(p);
425             }
426             //左旋
427             else if(heightDifference(p)==-2){
428                 Node nodeB=p.rchild;
429                 //如果b有左子节点，先将b右旋，再将a左旋
430                 if(nodeB.lchild!=null){
431                     rightRotation(nodeB);
432                     leftRotation(p);
433                 }
434                 //如果b无左子节点，a左旋
435                 else
436                     leftRotation(p);
437             }
438             p=p.father;
439         }
440     }
441 
442 
443 
444     public static void main(String args[]) {
445         AVLTree t=new AVLTree();
446         t.inseart(t.root,8);
447         t.inseart(t.root,5);
448         t.inseart(t.root,1);
449         t.inseart(t.root,11);
450         t.inseart(t.root,9);
451         t.printTree(t.root);
452         t.inseart(t.root,13);
453         t.printTree(t.root);
454         t.inseart(t.root,7);
455         t.inseart(t.root,6);
456         t.inseart(t.root,12);
457         t.printTree(t.root);
458         t.inseart(t.root,16);
459         t.printTree(t.root);
460 
461         //删值
462         //t.delete(t.root,9);
463         //t.printTree(t.root);
464         //t.delete(t.root,8);
465         //t.printTree(t.root);
466 //        t.delete(t.root,7);
467 //        t.printTree(t.root);
468         t.delete(t.root,5);
469         t.printTree(t.root);
470         t.delete(t.root,8);
471         t.printTree(t.root);
472 
473            //删最大值
474 //        t.deleteMax(t.root);
475 //        t.printTree(t.root);
476 //        t.deleteMax(t.root);
477 //        t.printTree(t.root);
478 //        t.deleteMax(t.root);
479 //        t.printTree(t.root);
480 //        t.deleteMax(t.root);
481 //        t.printTree(t.root);
482 
483 
484            //删最小值
485 //        t.deleteMin(t.root);
486 //        t.printTree(t.root);
487 //        t.deleteMin(t.root);
488 //        t.printTree(t.root);
489 //        t.deleteMin(t.root);
490 //        t.printTree(t.root);
491 //        t.deleteMin(t.root);
492 //        t.printTree(t.root);
493 
494         t.inOrder(t.root);
495     }
496 
497 
498 }

View Code

结语，虽然我的树状打印函数写的很捞，>4层之后误差较大，肉眼可见，但是调试的时候还是帮了大忙

 1 /**
 2      * 思路：先确定树高h-最后一层2^(h-1)个数，好知道根节点放在哪里（预留空间保证根再中间）
 3      * 设每个data三位数=space,元素之间空三位数，每行 (2^H+1)*3 个“ ”
 4      * _数_数_数_数_数_   每层2^(h-1)个数，2^(h-1)+1个space,最后一行长2^h+1个space
 5      *
 6      * 当层数多的时候稍乱，2333不想弄了，
 7      */
 8 
 9 /**辅助函数-从前一篇复制
10      * 求树高
11      * 打印树
12      */
13     //递归求树高-用于打印树
14     //递归
15     public int treeHeightRec(Node root){
16         if(root==null)
17             return 0;
18         else{
19             int a =treeHeightRec(root.lchild);
20             int b = treeHeightRec(root.rchild);
21             int a1=(a>b)?(a+1):(b+1);
22             return (a>b)?(a+1):(b+1);
23         }
24     }
25     //打印树--233，复制前一篇的方法，如果树层数很深时，打印的比较别扭
26     public void printTree(Node root){
27         int H=treeHeightRec(root);
28         int h=H;
29         //System.out.println("树高："+H);
30         if(H==0)
31             System.out.println("树空,无打印");
32         else{
33             System.out.println("打印树：");
34             Queue<Node> queue=new LinkedList<>();
35             queue.add(root);
36             int height=1;
37             //记录每层孩子个数
38             int len=1;
39             while(h>0){
40                 int length=0;
41                 String space="";
42                 for(int i=0;i<(((Math.pow(2,H)+1)*3)/(Math.pow(2,height)+1));i++)
43                     space+=" ";
44                 for(int i=0;i<len;i++){
45                     Node curroot=queue.poll();
46                     if(curroot.data==Integer.MAX_VALUE){
47                         System.out.print(space);
48                     }else
49                         System.out.print(space+curroot.data);
50 
51                     if(curroot.lchild!=null){
52                         queue.add(curroot.lchild);
53                     }
54                     else
55                         queue.add(new Node());
56                     length++;
57                     if(curroot.rchild!=null){
58                         queue.add(curroot.rchild);
59                     }
60                     else
61                         queue.add(new Node());
62                     length++;
63                 }
64                 System.out.println();
65                 System.out.println();
66                 len=length;
67                 height++;
68                 h--;
69             }
70             System.out.println();
71         }
72     }

View Code

查看全文

相关阅读:
Java集合源码分析（一）
EffectiveJava——请不要在代码中使用原生态类型
 Dubbo初探
 EffectiveJava——用函数对象表示策略
 EffectiveJava——类层次优于标签类
 notebook1.md
NoteBook学习（二）-------- Zeppelin简介与安装
 Spark2.0学习（三）--------核心API
Spark2.0学习（二）--------RDD详解
 Spark2.0学习（一）--------Spark简介

原文地址：https://www.cnblogs.com/wangpan8721/p/13706369.html