笔记1 -- The Learning Problem
最近在看NTU林轩田的《机器学习基石》课程,个人感觉讲的非常好。整个基石课程分成四个部分:
- When Can Machine Learn?
- Why Can Machine Learn?
- How Can Machine Learn?
- How Can Machine Learn Better?
每个部分由四节课组成,总共有16节课。那么,从这篇开始,我们将连续对这门课做课程笔记,共16篇,希望能对正在看这们课的童鞋有所帮助。下面开始第一节课的笔记:The Learning Problem。
一、What is Machine Learning
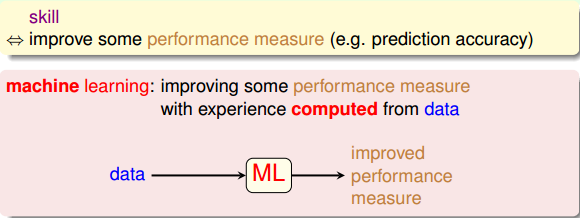
什么是“学习”?学习就是人类通过观察、积累经验,掌握某项技能或能力。就好像我们从小学习识别字母、认识汉字,就是学习的过程。而机器学习(Machine Learning),顾名思义,就是让机器(计算机)也能向人类一样,通过观察大量的数据和训练,发现事物规律,获得某种分析问题、解决问题的能力。

机器学习可以被定义为:Improving some performance measure with experence computed from data. 也就是机器从数据中总结经验,从数据中找出某种规律或者模型,并用它来解决实际问题。
什么情况下会使用机器学习来解决问题呢?其实,目前机器学习的应用非常广泛,基本上任何场合都能够看到它的身影。其应用场合大致可归纳为三个条件:
- 事物本身存在某种潜在规律
- 某些问题难以使用普通编程解决
- 有大量的数据样本可供使用

二、Applications of Machine Learning
机器学习在我们的衣、食、住、行、教育、娱乐等各个方面都有着广泛的应用,我们的生活处处都离不开机器学习。比如,打开购物网站,网站就会给我们自动推荐我们可能会喜欢的商品;电影频道会根据用户的浏览记录和观影记录,向不同用户推荐他们可能喜欢的电影等等,到处都有机器学习的影子。
三、Components of Machine Learning
本系列的课程对机器学习问题有一些基本的术语需要注意一下:
- 输入x
- 输出y
- 目标函数f,即最接近实际样本分布的规律
- 训练样本data
- 假设hypothesis,一个机器学习模型对应了很多不同的hypothesis,通过演算法A,选择一个最佳的hypothesis对应的函数称为矩g,g能最好地表示事物的内在规律,也是我们最终想要得到的模型表达式。

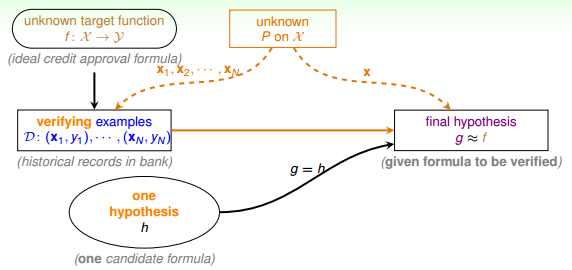
实际中,机器学习的流程图可以表示为:
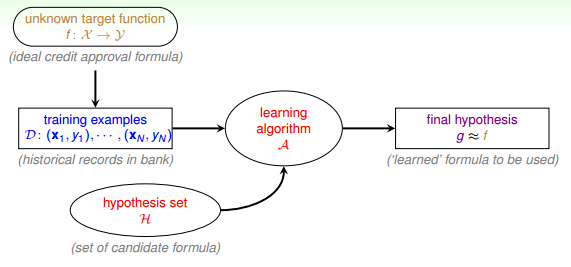
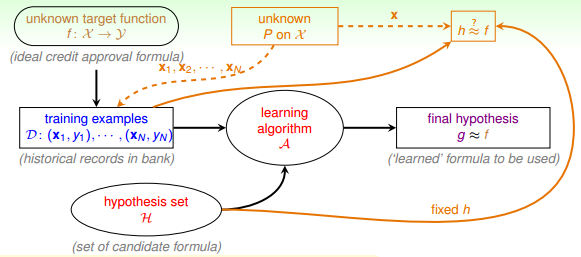
对于理想的目标函数f,我们是不知道的,我们手上拿到的是一些训练样本D,假设是监督式学习,其中有输入x,也有输出y。机器学习的过程,就是根据先验知识选择模型,该模型对应的hypothesis set(用H表示),H中包含了许多不同的hypothesis,通过演算法A,在训练样本D上进行训练,选择出一个最好的hypothes,对应的函数表达式g就是我们最终要求的。一般情况下,g能最接近目标函数f,这样,机器学习的整个流程就完成了。
四、Machine Learning and Other Fields
与机器学习相关的领域有:
- 数据挖掘(Data Mining)
- 人工智能(Artificial Intelligence)
- 统计(Statistics)
其实,机器学习与这三个领域是相通的,基本类似,但也不完全一样。机器学习是这三个领域中的有力工具,而同时,这三个领域也是机器学习可以广泛应用的领域,总得来说,他们之间没有十分明确的界线。
五、总结
本节课主要介绍了什么是机器学习,什么样的场合下可以使用机器学习解决问题,然后用流程图的形式展示了机器学习的整个过程,最后把机器学习和数据挖掘、人工智能、统计这三个领域做个比较。本节课的内容主要是概述性的东西,比较简单,所以笔记也相对比较简略。
笔记2 -- Learning to Answer Yes/No
上节课,我们主要简述了机器学习的定义及其重要性,并用流程图的形式介绍了机器学习的整个过程:根据模型H,使用演算法A,在训练样本D上进行训练,得到最好的h,其对应的g就是我们最后需要的机器学习的模型函数,一般g接近于目标函数f。本节课将继续深入探讨机器学习问题,介绍感知机Perceptron模型,并推导课程的第一个机器学习算法:Perceptron Learning Algorithm(PLA)。
一、Perceptron Hypothesis Set
引入这样一个例子:某银行要根据用户的年龄、性别、年收入等情况来判断是否给该用户发信用卡。现在有训练样本D,即之前用户的信息和是否发了信用卡。这是一个典型的机器学习问题,我们要根据D,通过A,在H中选择最好的h,得到g,接近目标函数f,也就是根据先验知识建立是否给用户发信用卡的模型。银行用这个模型对以后用户进行判断:发信用卡(+1),不发信用卡(-1)。
在这个机器学习的整个流程中,有一个部分非常重要:就是模型选择,即Hypothesis Set。选择什么样的模型,很大程度上会影响机器学习的效果和表现。下面介绍一个简单常用的Hypothesis Set:感知机(Perceptron)。
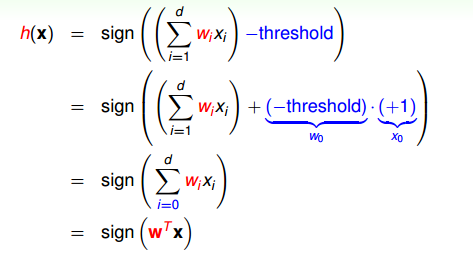
还是刚才银行是否给用户发信用卡的例子,我们把用户的个人信息作为特征向量x,令总共有d个特征,每个特征赋予不同的权重w,表示该特征对输出(是否发信用卡)的影响有多大。那所有特征的加权和的值与一个设定的阈值threshold进行比较:大于这个阈值,输出为+1,即发信用卡;小于这个阈值,输出为-1,即不发信用卡。感知机模型,就是当特征加权和与阈值的差大于或等于0,则输出h(x)=1;当特征加权和与阈值的差小于0,则输出h(x)=-1,而我们的目的就是计算出所有权值w和阈值threshold。

为了计算方便,通常我们将阈值threshold当做w0w0,引入一个x0=1x0=1的量与w0w0相乘,这样就把threshold也转变成了权值w0w0,简化了计算。h(x)的表达式做如下变换:
为了更清晰地说明感知机模型,我们假设Perceptrons在二维平面上,即h(x)=sign(w0+w1x1+w2x2)h(x)=sign(w0+w1x1+w2x2)。其中,w0+w1x1+w2x2=0w0+w1x1+w2x2=0是平面上一条分类直线,直线一侧是正类(+1),直线另一侧是负类(-1)。权重w不同,对应于平面上不同的直线。

那么,我们所说的Perceptron,在这个模型上就是一条直线,称之为linear(binary) classifiers。注意一下,感知器线性分类不限定在二维空间中,在3D中,线性分类用平面表示,在更高维度中,线性分类用超平面表示,即只要是形如wTxwTx的线性模型就都属于linear(binary) classifiers。
同时,需要注意的是,这里所说的linear(binary) classifiers是用简单的感知器模型建立的,线性分类问题还可以使用logistic regression来解决,后面将会介绍。
二、Perceptron Learning Algorithm(PLA)
根据上一部分的介绍,我们已经知道了hypothesis set由许多条直线构成。接下来,我们的目的就是如何设计一个演算法A,来选择一个最好的直线,能将平面上所有的正类和负类完全分开,也就是找到最好的g,使g≈fg≈f。
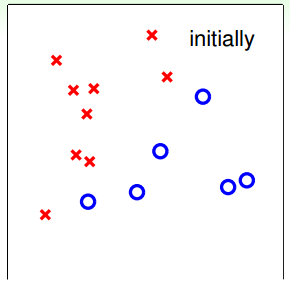
如何找到这样一条最好的直线呢?我们可以使用逐点修正的思想,首先在平面上随意取一条直线,看看哪些点分类错误。然后开始对第一个错误点就行修正,即变换直线的位置,使这个错误点变成分类正确的点。接着,再对第二个、第三个等所有的错误分类点就行直线纠正,直到所有的点都完全分类正确了,就得到了最好的直线。这种“逐步修正”,就是PLA思想所在。

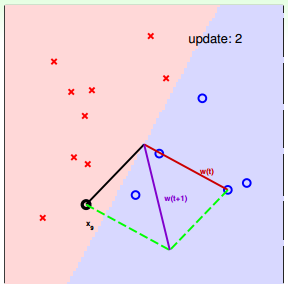
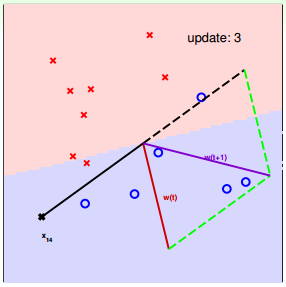
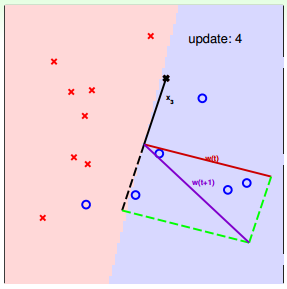
下面介绍一下PLA是怎么做的。首先随机选择一条直线进行分类。然后找到第一个分类错误的点,如果这个点表示正类,被误分为负类,即wTtxn(t)<0wtTxn(t)<0,那表示w和x夹角大于90度,其中w是直线的法向量。所以,x被误分在直线的下侧(相对于法向量,法向量的方向即为正类所在的一侧),修正的方法就是使w和x夹角小于90度。通常做法是w←w+yx, y=1w←w+yx, y=1,如图右上角所示,一次或多次更新后的w+yxw+yx与x夹角小于90度,能保证x位于直线的上侧,则对误分为负类的错误点完成了直线修正。
同理,如果是误分为正类的点,即wTtxn(t)>0wtTxn(t)>0,那表示w和x夹角小于90度,其中w是直线的法向量。所以,x被误分在直线的上侧,修正的方法就是使w和x夹角大于90度。通常做法是w←w+yx, y=−1w←w+yx, y=−1,如图右下角所示,一次或多次更新后的w+yxw+yx与x夹角大于90度,能保证x位于直线的下侧,则对误分为正类的错误点也完成了直线修正。
按照这种思想,遇到个错误点就进行修正,不断迭代。要注意一点:每次修正直线,可能使之前分类正确的点变成错误点,这是可能发生的。但是没关系,不断迭代,不断修正,最终会将所有点完全正确分类(PLA前提是线性可分的)。这种做法的思想是“知错能改”,有句话形容它:“A fault confessed is half redressed.”
实际操作中,可以一个点一个点地遍历,发现分类错误的点就进行修正,直到所有点全部分类正确。这种被称为Cyclic PLA。

下面用图解的形式来介绍PLA的修正过程:

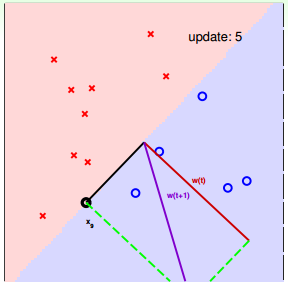
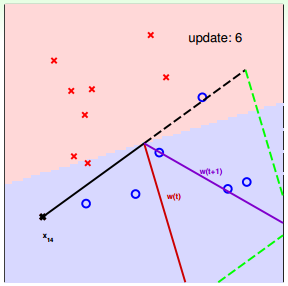
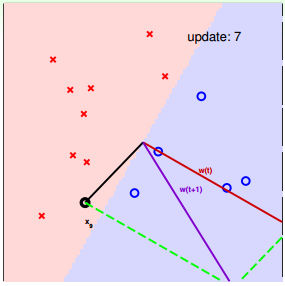


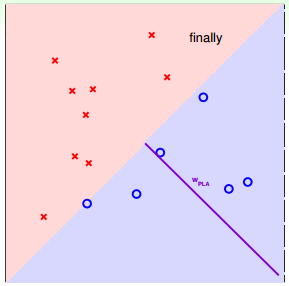
对PLA,我们需要考虑以下两个问题:
- PLA迭代一定会停下来吗?如果线性不可分怎么办?
- PLA停下来的时候,是否能保证f≈gf≈g?如果没有停下来,是否有f≈gf≈g?
三、Guarantee of PLA
PLA什么时候会停下来呢?根据PLA的定义,当找到一条直线,能将所有平面上的点都分类正确,那么PLA就停止了。要达到这个终止条件,就必须保证D是线性可分(linear separable)。如果是非线性可分的,那么,PLA就不会停止。

对于线性可分的情况,如果有这样一条直线,能够将正类和负类完全分开,令这时候的目标权重为wfwf,则对每个点,必然满足yn=sign(wTfxn)yn=sign(wfTxn),即对任一点:

PLA会对每次错误的点进行修正,更新权重wt+1wt+1的值,如果wt+1wt+1与wfwf越来越接近,数学运算上就是内积越大,那表示wt+1wt+1是在接近目标权重wfwf,证明PLA是有学习效果的。所以,我们来计算wt+1wt+1与wfwf的内积:
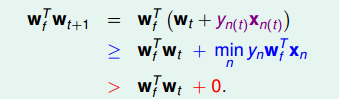
从推导可以看出,wt+1wt+1与wfwf的内积跟wtwt与wfwf的内积相比更大了。似乎说明了wt+1wt+1更接近wfwf,但是内积更大,可能是向量长度更大了,不一定是向量间角度更小。所以,下一步,我们还需要证明wt+1wt+1与wtwt向量长度的关系:
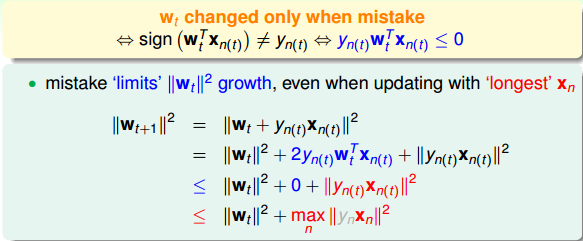
wtwt只会在分类错误的情况下更新,最终得到的||w2t+1||||wt+12||相比||w2t||||wt2||的增量值不超过max||x2n||max||xn2||。也就是说,wtwt的增长被限制了,wt+1wt+1与wtwt向量长度不会差别太大!
如果令初始权值w0=0w0=0,那么经过T次错误修正后,有如下结论:
wTf||wf||wTwT≥T−−√⋅constantwfT||wf||wTwT≥T⋅constant
下面贴出来该结论的具体推导过程:

上述不等式左边其实是wTwT与wfwf夹角的余弦值,随着T增大,该余弦值越来越接近1,即wTwT与wfwf越来越接近。同时,需要注意的是,T−−√⋅constant≤1T⋅constant≤1,也就是说,迭代次数T是有上界的。根据以上证明,我们最终得到的结论是:wt+1wt+1与wfwf的是随着迭代次数增加,逐渐接近的。而且,PLA最终会停下来(因为T有上界),实现对线性可分的数据集完全分类。
四、Non-Separable Data
上一部分,我们证明了线性可分的情况下,PLA是可以停下来并正确分类的,但对于非线性可分的情况,wfwf实际上并不存在,那么之前的推导并不成立,PLA不一定会停下来。所以,PLA虽然实现简单,但也有缺点:

对于非线性可分的情况,我们可以把它当成是数据集D中掺杂了一下noise,事实上,大多数情况下我们遇到的D,都或多或少地掺杂了noise。这时,机器学习流程是这样的:

在非线性情况下,我们可以把条件放松,即不苛求每个点都分类正确,而是容忍有错误点,取错误点的个数最少时的权重w:
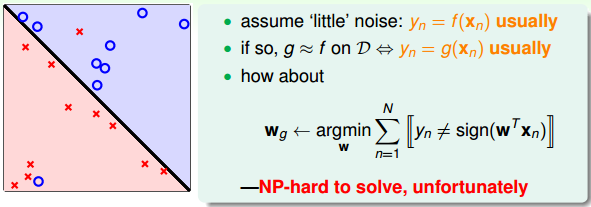
事实证明,上面的解是NP-hard问题,难以求解。然而,我们可以对在线性可分类型中表现很好的PLA做个修改,把它应用到非线性可分类型中,获得近似最好的g。
修改后的PLA称为Packet Algorithm。它的算法流程与PLA基本类似,首先初始化权重w0w0,计算出在这条初始化的直线中,分类错误点的个数。然后对错误点进行修正,更新w,得到一条新的直线,在计算其对应的分类错误的点的个数,并与之前错误点个数比较,取个数较小的直线作为我们当前选择的分类直线。之后,再经过n次迭代,不断比较当前分类错误点个数与之前最少的错误点个数比较,选择最小的值保存。直到迭代次数完成后,选取个数最少的直线对应的w,即为我们最终想要得到的权重值。

如何判断数据集D是不是线性可分?对于二维数据来说,通常还是通过肉眼观察来判断的。一般情况下,Pocket Algorithm要比PLA速度慢一些。
五、总结
本节课主要介绍了线性感知机模型,以及解决这类感知机分类问题的简单算法:PLA。我们详细证明了对于线性可分问题,PLA可以停下来并实现完全正确分类。对于不是线性可分的问题,可以使用PLA的修正算法Pocket Algorithm来解决。
笔记3 -- Types of Learning
上节课我们主要介绍了解决线性分类问题的一个简单的方法:PLA。PLA能够在平面中选择一条直线将样本数据完全正确分类。而对于线性不可分的情况,可以使用Pocket Algorithm来处理。本节课将主要介绍一下机器学习有哪些种类,并进行归纳。
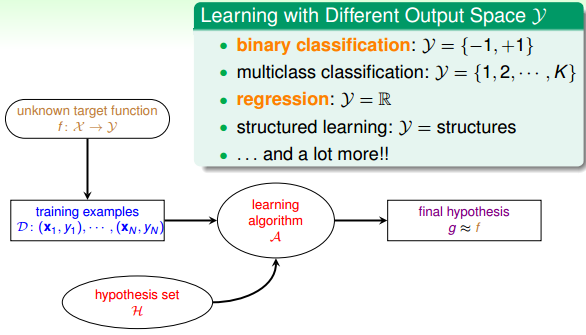
一、Learning with Different Output Space Y
我们在上节课引入的银行根据用户个人情况判断是否给他发信用卡的例子,这是一个典型的二元分类(binary classification)问题。也就是说输出只有两个,一般y={-1, +1},-1代表不发信用卡(负类),+1代表发信用卡(正类)。
二元分类的问题很常见,包括信用卡发放、垃圾邮件判别、患者疾病诊断、答案正确性估计等等。二元分类是机器学习领域非常核心和基本的问题。二元分类有线性模型也有非线性模型,根据实际问题情况,选择不同的模型。
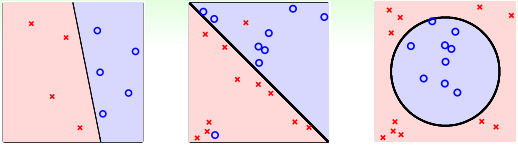
除了二元分类,也有多元分类(Multiclass Classification)问题。顾名思义,多元分类的输出多于两个,y={1, 2, … , K}, K>2. 一般多元分类的应用有数字识别、图片内容识别等等。

二元分类和多元分类都属于分类问题,它们的输出都是离散值。二对于另外一种情况,比如训练模型,预测房屋价格、股票收益多少等,这类问题的输出y=R,即范围在整个实数空间,是连续的。这类问题,我们把它叫做回归(Regression)。最简单的线性回归是一种典型的回归模型。
除了分类和回归问题,在自然语言处理等领域中,还会用到一种机器学习问题:结构化学习(Structured Learning)。结构化学习的输出空间包含了某种结构在里面,它的一些解法通常是从多分类问题延伸而来的,比较复杂。本系列课程不会详细介绍Structured Learning,有兴趣的读者可以自行对它进行更深入的研究。
简单总结一下,机器学习按照输出空间划分的话,包括二元分类、多元分类、回归、结构化学习等不同的类型。其中二元分类和回归是最基础、最核心的两个类型,也是我们课程主要介绍的部分。
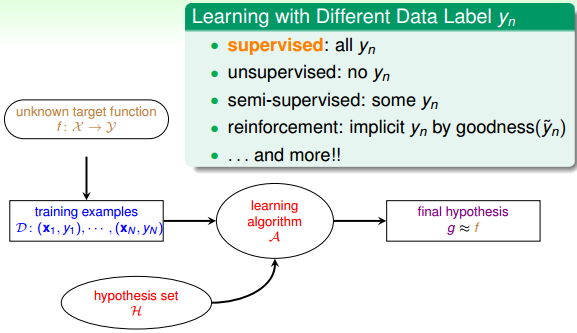
二、Learning with Different Data Label yn
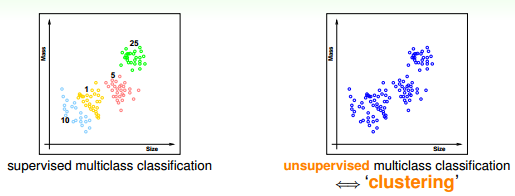
如果我们拿到的训练样本D既有输入特征x,也有输出yn,那么我们把这种类型的学习称为监督式学习(Supervised Learning)。监督式学习可以是二元分类、多元分类或者是回归,最重要的是知道输出标签yn。与监督式学习相对立的另一种类型是非监督式学习(Unsupervised learning)。非监督式学习是没有输出标签yn的,典型的非监督式学习包括:聚类(clustering)问题,比如对网页上新闻的自动分类;密度估计,比如交通路况分析;异常检测,比如用户网络流量监测。通常情况下,非监督式学习更复杂一些,而且非监督的问题很多都可以使用监督式学习的一些算法思想来实现。
介于监督式和非监督式学习之间的叫做半监督式学习(Semi-supervised Learning)。顾名思义,半监督式学习就是说一部分数据有输出标签yn,而另一部分数据没有输出标签yn。在实际应用中,半监督式学习有时候是必须的,比如医药公司对某些药物进行检测,考虑到成本和实验人群限制等问题,只有一部分数据有输出标签yn。
监督式、非监督式、半监督式学习是机器学习领域三个主要类型。除此之外,还有一种非常重要的类型:增强学习(Reinforcement Learning)。增强学习中,我们给模型或系统一些输入,但是给不了我们希望的真实的输出y,根据模型的输出反馈,如果反馈结果良好,更接近真实输出,就给其正向激励,如果反馈结果不好,偏离真实输出,就给其反向激励。不断通过“反馈-修正”这种形式,一步一步让模型学习的更好,这就是增强学习的核心所在。增强学习可以类比成训练宠物的过程,比如我们要训练狗狗坐下,但是狗狗无法直接听懂我们的指令“sit down”。在训练过程中,我们给狗狗示意,如果它表现得好,我们就给他奖励,如果它做跟sit down完全无关的动作,我们就给它小小的惩罚。这样不断修正狗狗的动作,最终能让它按照我们的指令来行动。实际生活中,增强学习的例子也很多,比如根据用户点击、选择而不断改进的广告系统
简单总结一下,机器学习按照数据输出标签yn划分的话,包括监督式学习、非监督式学习、半监督式学习和增强学习等。其中,监督式学习应用最为广泛。
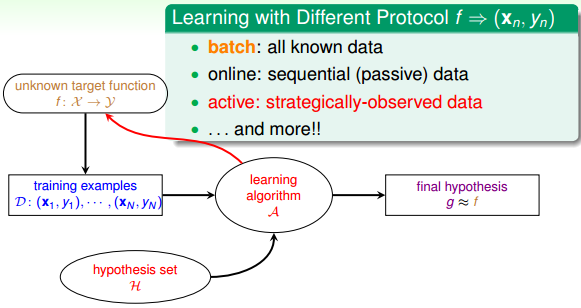
三、Learning with Different Protocol f(xn,yn)
按照不同的协议,机器学习可以分为三种类型:
- Batch Learning
- Online
- Active Learning
batch learning是一种常见的类型。batch learning获得的训练数据D是一批的,即一次性拿到整个D,对其进行学习建模,得到我们最终的机器学习模型。batch learning在实际应用中最为广泛。
online是一种在线学习模型,数据是实时更新的,根据数据一个个进来,同步更新我们的算法。比如在线邮件过滤系统,根据一封一封邮件的内容,根据当前算法判断是否为垃圾邮件,再根据用户反馈,及时更新当前算法。这是一个动态的过程。之前我们介绍的PLA和增强学习都可以使用online模型。
active learning是近些年来新出现的一种机器学习类型,即让机器具备主动问问题的能力,例如手写数字识别,机器自己生成一个数字或者对它不确定的手写字主动提问。active learning优势之一是在获取样本label比较困难的时候,可以节约时间和成本,只对一些重要的label提出需求。
简单总结一下,按照不同的协议,机器学习可以分为batch, online, active。这三种学习类型分别可以类比为:填鸭式,老师教学以及主动问问题。
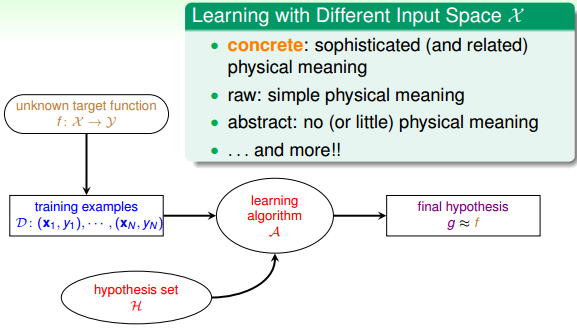
四、Learning with Different Input Space X
上面几部分介绍的机器学习分类都是根据输出来分类的,比如根据输出空间进行分类,根据输出y的标记进行分类,根据取得数据和标记的方法进行分类。这部分,我们将谈谈输入X有哪些类型。
输入X的第一种类型就是concrete features。比如说硬币分类问题中硬币的尺寸、重量等;比如疾病诊断中的病人信息等具体特征。concrete features对机器学习来说最容易理解和使用。
第二种类型是raw features。比如说手写数字识别中每个数字所在图片的mxn维像素值;比如语音信号的频谱等。raw features一般比较抽象,经常需要人或者机器来转换为其对应的concrete features,这个转换的过程就是Feature Transform。
第三种类型是abstract features。比如某购物网站做购买预测时,提供给参赛者的是抽象加密过的资料编号或者ID,这些特征X完全是抽象的,没有实际的物理含义。所以对于机器学习来说是比较困难的,需要对特征进行更多的转换和提取。
简单总结一下,根据输入X类型不同,可以分为concetet, raw, abstract。将一些抽象的特征转换为具体的特征,是机器学习过程中非常重要的一个环节。在《机器学习技法》课程中,我们再详细介绍。
五、总结:
本节课主要介绍了机器学习的类型,包括Out Space、Data Label、Protocol、Input Space四种类型。

笔记4 -- Feasibility of Learning
上节课,我们主要介绍了根据不同的设定,机器学习可以分为不同的类型。其中,监督式学习中的二元分类和回归分析是最常见的也是最重要的机器学习问题。本节课,我们将介绍机器学习的可行性,讨论问题是否可以使用机器学习来解决。
一、Learning is Impossible
首先,考虑这样一个例子,如下图所示,有3个label为-1的九宫格和3个label为+1的九宫格。根据这6个样本,提取相应label下的特征,预测右边九宫格是属于-1还是+1?结果是,如果依据对称性,我们会把它归为+1;如果依据九宫格左上角是否是黑色,我们会把它归为-1。除此之外,还有根据其它不同特征进行分类,得到不同结果的情况。而且,这些分类结果貌似都是正确合理的,因为对于6个训练样本来说,我们选择的模型都有很好的分类效果。
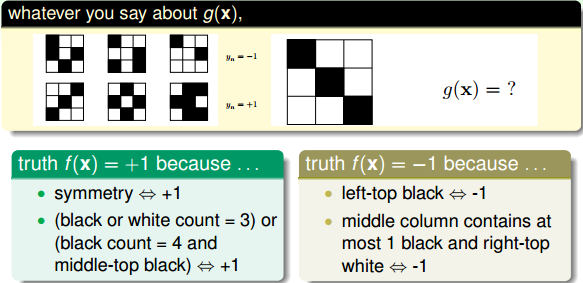
再来看一个比较数学化的二分类例子,输入特征x是二进制的、三维的,对应有8种输入,其中训练样本D有5个。那么,根据训练样本对应的输出y,假设有8个hypothesis,这8个hypothesis在D上,对5个训练样本的分类效果效果都完全正确。但是在另外3个测试数据上,不同的hypothesis表现有好有坏。在已知数据D上,g≈fg≈f;但是在D以外的未知数据上,g≈fg≈f不一定成立。而机器学习目的,恰恰是希望我们选择的模型能在未知数据上的预测与真实结果是一致的,而不是在已知的数据集D上寻求最佳效果。
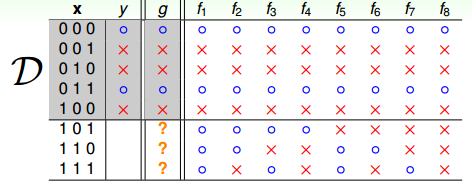
这个例子告诉我们,我们想要在D以外的数据中更接近目标函数似乎是做不到的,只能保证对D有很好的分类结果。机器学习的这种特性被称为没有免费午餐(No Free Lunch)定理。NFL定理表明没有一个学习算法可以在任何领域总是产生最准确的学习器。不管采用何种学习算法,至少存在一个目标函数,能够使得随机猜测算法是更好的算法。平常所说的一个学习算法比另一个算法更“优越”,效果更好,只是针对特定的问题,特定的先验信息,数据的分布,训练样本的数目,代价或奖励函数等。从这个例子来看,NFL说明了无法保证一个机器学习算法在D以外的数据集上一定能分类或预测正确,除非加上一些假设条件,我们以后会介绍。
二、Probability to the Rescue
从上一节得出的结论是:在训练集D以外的样本上,机器学习的模型是很难,似乎做不到正确预测或分类的。那是否有一些工具或者方法能够对未知的目标函数f做一些推论,让我们的机器学习模型能够变得有用呢?
如果有一个装有很多(数量很大数不过来)橙色球和绿色球的罐子,我们能不能推断橙色球的比例u?统计学上的做法是,从罐子中随机取出N个球,作为样本,计算这N个球中橙色球的比例v,那么就估计出罐子中橙色球的比例约为v。

这种随机抽取的做法能否说明罐子里橙色球的比例一定是v呢?答案是否定的。但是从概率的角度来说,样本中的v很有可能接近我们未知的u。下面从数学推导的角度来看v与u是否相近。
已知u是罐子里橙色球的比例,v是N个抽取的样本中橙色球的比例。当N足够大的时候,v接近于u。这就是Hoeffding’s inequality:
P[|v−u|>ϵ]≤2exp(−2ϵ2N)P[|v−u|>ϵ]≤2exp(−2ϵ2N)
Hoeffding不等式说明当N很大的时候,v与u相差不会很大,它们之间的差值被限定在ϵϵ之内。我们把结论v=u称为probably approximately correct(PAC)。

三、Connection to Learning
下面,我们将罐子的内容对应到机器学习的概念上来。机器学习中hypothesis与目标函数相等的可能性,类比于罐子中橙色球的概率问题;罐子里的一颗颗弹珠类比于机器学习样本空间的x;橙色的弹珠类比于h(x)与f不相等;绿色的弹珠类比于h(x)与f相等;从罐子中抽取的N个球类比于机器学习的训练样本D,且这两种抽样的样本与总体样本之间都是独立同分布的。所以呢,如果样本N够大,且是独立同分布的,那么,从样本中h(x)≠f(x)h(x)≠f(x)的概率就能推导在抽样样本外的所有样本中h(x)≠f(x)h(x)≠f(x)的概率是多少。

映射中最关键的点是讲抽样中橙球的概率理解为样本数据集D上h(x)错误的概率,以此推算出在所有数据上h(x)错误的概率,这也是机器学习能够工作的本质,即我们为啥在采样数据上得到了一个假设,就可以推到全局呢?因为两者的错误率是PAC的,只要我们保证前者小,后者也就小了。
这里我们引入两个值Ein(h)Ein(h)和Eout(h)Eout(h)。Ein(h)Ein(h)表示在抽样样本中,h(x)与ynyn不相等的概率;Eout(h)Eout(h)表示实际所有样本中,h(x)与f(x)不相等的概率是多少。
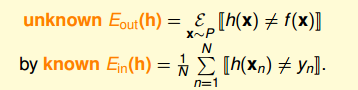
同样,它的Hoeffding’s inequality可以表示为:
P[|Ein(h)−Eout(h)|>ϵ]≤2exp(−2ϵ2N)P[|Ein(h)−Eout(h)|>ϵ]≤2exp(−2ϵ2N)
该不等式表明,Ein(h)=Eout(h)Ein(h)=Eout(h)也是PAC的。如果Ein(h)≈Eout(h)Ein(h)≈Eout(h),Ein(h)Ein(h)很小,那么就能推断出Eout(h)Eout(h)很小,也就是说在该数据分布P下,h与f非常接近,机器学习的模型比较准确。
一般地,h如果是固定的,N很大的时候,Ein(h)≈Eout(h)Ein(h)≈Eout(h),但是并不意味着g≈fg≈f。因为h是固定的,不能保证Ein(h)Ein(h)足够小,即使Ein(h)≈Eout(h)Ein(h)≈Eout(h),也可能使Eout(h)Eout(h)偏大。所以,一般会通过演算法A,选择最好的h,使Ein(h)Ein(h)足够小,从而保证Eout(h)Eout(h)很小。固定的h,使用新数据进行测试,验证其错误率是多少。
四、Connection to Real Learning

假设现在有很多罐子M个(即有M个hypothesis),如果其中某个罐子抽样的球全是绿色,那是不是应该选择这个罐子呢?我们先来看这样一个例子:150个人抛硬币,那么其中至少有一个人连续5次硬币都是正面朝上的概率是
1−(3132)150>99%1−(3132)150>99%
可见这个概率是很大的,但是能否说明5次正面朝上的这个硬币具有代表性呢?答案是否定的!并不能说明该硬币单次正面朝上的概率很大,其实都是0.5。一样的道理,抽到全是绿色求的时候也不能一定说明那个罐子就全是绿色球。当罐子数目很多或者抛硬币的人数很多的时候,可能引发Bad Sample,Bad Sample就是EinEin和EoutEout差别很大,即选择过多带来的负面影响,选择过多会恶化不好的情形。
根据许多次抽样的到的不同的数据集D,Hoeffding’s inequality保证了大多数的D都是比较好的情形(即对于某个h,保证Ein≈EoutEin≈Eout),但是也有可能出现Bad Data,即EinEin和EoutEout差别很大的数据集D,这是小概率事件。
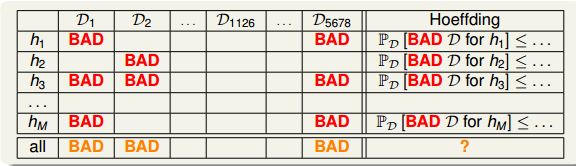
也就是说,不同的数据集DnDn,对于不同的hypothesis,有可能成为Bad Data。只要DnDn在某个hypothesis上是Bad Data,那么DnDn就是Bad Data。只有当DnDn在所有的hypothesis上都是好的数据,才说明DnDn不是Bad Data,可以自由选择演算法A进行建模。那么,根据Hoeffding’s inequality,Bad Data的上界可以表示为连级(union bound)的形式:
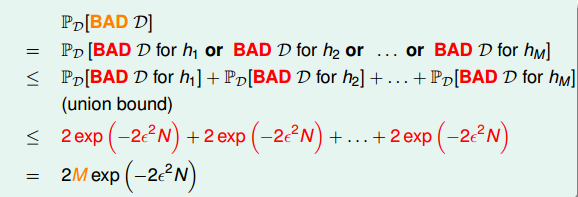
其中,M是hypothesis的个数,N是样本D的数量,ϵϵ是参数。该union bound表明,当M有限,且N足够大的时候,Bad Data出现的概率就更低了,即能保证D对于所有的h都有Ein≈EoutEin≈Eout,满足PAC,演算法A的选择不受限制。那么满足这种union bound的情况,我们就可以和之前一样,选取一个合理的演算法(PLA/pocket),选择使EinEin最小的hmhm作为矩g,一般能够保证g≈fg≈f,即有不错的泛化能力。
所以,如果hypothesis的个数M是有限的,N足够大,那么通过演算法A任意选择一个矩g,都有Ein≈EoutEin≈Eout成立;同时,如果找到一个矩g,使Ein≈0Ein≈0,PAC就能保证Eout≈0Eout≈0。至此,就证明了机器学习是可行的。

但是,如上面的学习流程图右下角所示,如果M是无数个,例如之前介绍的PLA直线有无数条,是否这些推论就不成立了呢?是否机器就不能进行学习呢?这些内容和问题,我们下节课再介绍。
五、总结
本节课主要介绍了机器学习的可行性。首先引入NFL定理,说明机器学习无法找到一个矩g能够完全和目标函数f一样。接着介绍了可以采用一些统计上的假设,例如Hoeffding不等式,建立EinEin和EoutEout的联系,证明对于某个h,当N足够大的时候,EinEin和EoutEout是PAC的。最后,对于h个数很多的情况,只要有h个数M是有限的,且N足够大,就能保证Ein≈EoutEin≈Eout,证明机器学习是可行的。