Differential expression analysis for paired RNA-seq data
抽象
背景:
RNA-Seq技术通过产生序列读数并在不同生物条件下计数其频率来测量转录本丰度。
为了鉴定两种条件之间差异表达的基因,重要的是要考虑实验设计以及数据的分布特性。
在许多RNA-Seq研究中,表达数据以多对获得,例如来自相同个体的治疗前和治疗后样品。
我们寻求将配对结构纳入分析。
结果:
我们提出了一个用于RNA-Seq数据的贝叶斯分层混合模型,以分别考虑变异性
来自配对数据结构的个体内部和之间。
该方法假定与伽马分布混合的数据的泊松分布以考虑对之间的可变性。
差异表达的影响由双组分混合模型建模。
通过模拟和实际数据检查该方法的性能。
结论:
在此设置中,我们提出的模型比现有方法提供更高的灵敏度来检测差异表达。
对真实RNA-Seq数据的应用证明了该方法用于检测具有低平均表达水平或较短转录物长度的基因的表达改变的有用性。
背景
常规收集基因表达谱以鉴定跨不同个体和细胞状态的差异表达的基因和途径。基于测序的技术与其他技术相比,可以更准确地量化表达水平。早期基于序列
表达通过计数从转录本的3'末端产生的称为标签的短片段测量转录本丰度。基于标签的方法包括基因表达的系列分析(SAGE,[1]),基因表达(CAGE),LongSAGE和大规模平行签名测序(MPSS)的Cap分析。深度测序技术的发展使得能够同时对数百万个分子进行测序,并导致了先进的表达测量方法[2,3]。数字基因表达 - 标签分析[4]采用基于标签的方法与'下一代'一起使用测序平台。RNA-Seq是一种替代方法,即“全基因组鸟枪测序”的应用。简而言之,它需要通过随机引发片段化RNA来产生cDNA文库。然后对cDNA文库进行下一代测序,以产生对应于该文库的短核苷酸序列(读段)cDNA片段的末端。RNA-Seq旨在衡量整个转录组,优于微阵列和基于标签的方法,因为它提供了更多信息例如选择性剪接和异构体特异性基因表达,具有非常低的背景信号和
更广泛的动态量化范围[5]。此外,最近的实验揭示了RNA-Seq的测量方法表达水平具有高准确性和可重复性[6-9]。
基于序列的方法将基因表达量化为“数字”计数,并且需要适合的建模计数随机变量。
泊松分布一直是建模表达数据的核心[10-12],并且通常应用于RNA-Seq数据[6,13]。尤其是李等人。 (2012)提出了一种基于排列的方法来生成零分布[14]。然而,
基于泊松的方法可能不会考虑生物样本之间的所有变化。提出了Beta-Binomial分层模型[15,16],过度分散的logistic [17]和过度分散的对数线性模型[18],分别捕获每个基因的额外方差。
已经提出负双生物模型通过收缩估计来估计过度离散参数[19-21],均值依赖局部回归[22],
或经验导出的先验分布[23]。或者,在贝叶斯建模框架下提出了β二项式[24]和泊松混合[25]模型。还考虑了重采样的非参数方法[26]。这些方法通常假定两组样品是独立获得的。
最近,这些方法中的一些已经扩展到处理多因素设计结构[14,16,21,22]。许多实用的RNA测序研究收集配对结构的数据,其中在将治疗应用于同一个体之前和之后测量全局表达谱。适当建模此类数据需要考虑这种设计结构以及数据的分布特性。泊松模型已被用于测试药物的影响观察发生在配对数据中,如前药和药物后计数[27]。李[28]考虑了混合物模型,以解释个人之间的额外差异,超出预期的水平泊松模型。
这些方法假设成对观察的独立性取决于个体均值。双变量泊松或负二项分布是模拟观测之间相关性的替代选择[29,30]。在本文中,我们提出了一种贝叶斯分层方法来分别建模配对计数数据
说明配对数据结构中的个体差异之间和之间的差异。
我们的工作采用Poisson-Gamma混合模型[28]并利用贝叶斯方法来评估表达差异。我们注意到贝叶斯模型被广泛用于微阵列研究并且具有改进的检测灵敏度
通过在基因之间共享信息来区分差异基因[31]。混合物模型也常用于模拟差异表达,其中非差异表达和不同表达的基因对应于不同的混合物组分。
在文献中已经考虑了各种混合物模型规格。伽玛和对数正态分布用于模拟表达水平[32,33]。Smyth [34]假设点的质量为零,因为对数标度的倍数变化为
对于非空基因,无效基因和以零为中心的正态分布。Lonnstedt等人。 [35]和戈塔多等。 [36]提出了两个(null和nonnull)或三个normal(null,over和under表达式)的混合
分布。非参数方法有也被利用[31,37]。Lewin等人。 [38]讨论了混合物组件先验和模型检查的各种选择。
本手稿的其余部分安排如下。数据部分介绍了促进这项研究的生物学问题和数据。方法部分介绍我们的参数模型和贝叶斯方法,以识别具有差异表达水平的基因。
通过模拟检查所提出的模型的性能。进行了两组模拟研究:(1)基于模型假设的方法来研究所提出的方法对参数估计的准确性,以及(2)基于模仿激励数据集进行检查的那些
所提方法的鲁棒性。最后,将所提出的方法应用于具有详细的实际数据讨论结果并与其他方法进行比较。
数据钱等。 (Qian F.等人:使用RNASeq分析鉴定对西尼罗病毒感染具有抗性的基因,提交)设计了RNA-Seq实验来研究人类西尼罗河病毒(WNV)感染。该研究的一个目的是鉴定来自原发性人的病毒感染的改变的基因/转录物与未感染的样品相比,巨噬细胞。
该研究自然具有成对的设计结构。根据耶鲁大学人类研究保护计划的指导方针,共招募了10名健康捐献者,并从新鲜肝素化中分离出细胞。如前所述[39]用于感染UVV(菌株CT2741,MOI = 1,24小时)的血液样品。PolyA + RNA由未感染和WNV感染制备原代巨噬细胞,片段化,并使用Illumina Genome Analyzer2进行测序。从每个样品中获得大约5000万个质量过滤读数,并且映射了大约85%使用TOPHAT v.1.1.4对含有ENSEMBL转录本注释(第57版)的人类转录组(hg19)[40]。通过基于最大似然法的方法对基因和转录物同种型进行评分以进行表达在Cufflinks v.0.9.3 [41]。为了分析差异表达,首先将数据从FPKM单元(每千位片段的每千碱基片段的片段)转换为源自每种转录物同种型的读数的数量。修剪平均法[42]是用于进一步规范化计数表达式值。处理的数据包含来自总共20个样品的转录物水平表达计数,所述样品由10对未感染和病毒感染的样品组成。对于差异表达分析,我们删除了较少的成绩单10个未感染样品的总计数超过10个,或未感染条件下6个或更多个体未观察到计数。完成这些步骤后,37,111份转录本被考虑用于数据分析。
方法
贝叶斯混合模型用于配对计数我们现在描述我们的贝叶斯分层混合模型,以从配对的RNA-seq数据中鉴定差异表达的基因/转录物。
如上所述,这些数据自然地来自测量来自治疗的生物学变化的实验。我们从过度分散的计数开始模型[28]。
对于基因g = 1,观察结果用一对(Ygi1,Ygi2)表示。 。 。 ,G和个人i = 1 ,. 。 。 ,n,其中Ygi1是观察到的基线表达水平,Ygi2是处理后观察到的水平。文库的大小分别表示为Ni1和Ni2。
设λgi表示相对于库大小的真实基线表达式。然后,Ygi1可以被建模为具有平均值λgiNi1的泊松随机变量。设χg表示处理后表达水平倍数变化,因此真实表达水平为χgλgiNi2,则Ygi2可以建模为具有平均值χgλgiNi2的泊松随机变量。我们的目标是测试是否有任何治疗效果,即χg= 1,其中Ygi1 |λgi,χg~泊松(Ni1λgi),Ygi2 |λgi,χg~泊松(Ni2λgiχg)。(1)已经证明技术之间存在差异可以通过泊松分布[6]捕获RNA-Seq数据的重复。但是,更大的差异可以如果从具有基础生物系统差异的个体收集观察结果,则应该预期。在Poisson计数中模拟过度离散的一种方法是将其与Gamma分布混合[28]。在这个模型中,我们使用Gamma分布来模拟具有形状参数αg和速率βg的个体的基线预期表达式λgi;
fλ(λgi)=
β
αG
G
(αg)
λ
αG-1
gi e-βgλgi。
(2)
该模型允许我们获得更简单的预测密度形式,即可以整合出λgi
(参见附录)。
假设基线表达和治疗效果之间存在独立性,我们使用双组分混合模型来表征倍数变化分布,
其中每个基因的表达变化状态由潜变量zg定义,其中zg = 0对应于无变化,否则zg = 1。
我们假设zg对于相等的表达式具有π0的概率,即zg = 0,
差分表达式的概率为π1= 1 - π0。
给定状态0或1,假设对数缩放的倍数变化遵循正态分布。
在相等的表达式下,假定对数倍变化来自a
正态分布以零和方差σ20为中心。
对于具有差异表达的基因,
如果我们假设他们的logfold
变化遵循以零为中心的正态分布,
我们隐含地假设基因有过高或低表达的平等机会。然而,
在病毒感染后,对于前面描述的数据集,更多的基因表达不足,3.2%的转录物表达后表达增加超过4倍。
感染率为4.3%,减少幅度超过4倍。为了适应这种不对称性,我们假设非空基因的对数倍变化来自正常
分布均值为μ1,
可能与0不同,
和方差σ21。
log(χg)|(zg = 0)〜正常(0,σ2
0)
log(χg)|(zg = 1)〜正常(μ1,σ2
1)
收集到目前为止讨论的所有组件,该模型可以总结在图1中。
根据这个设置,
目标是估计特定基因在治疗后差异表达的后验概率,即,
Pr(zg = 1 |数据)。然后根据可以将基因推断为DE(差异表达)或EE(等同表达)
这些概率。
为了完成我们的模型描述,我们需要为未知模型参数指定先前的假设,
θ=({αg},{βg},π0,π1,σ2
0,μ1,σ21)。
在我们的实施中,
我们假设这些未知参数的非信息先验:
1.(π0,π1)~Dirichlet(1,1),即π0~Uniform(0,1)。
2.每个αg和βg都有一个无信息的先验。
3. p(σ20)α1/σ2
0和p(σ21)α1/σ21。
4.μ1有一个不正确的先验。
5.所有参数之间的联合独立性。
通过马尔可夫链蒙特卡罗(MCMC)进行参数估计
在本节中,我们描述了Gibbs采样算法[43],我们用它来迭代地对模型参数进行采样
根据其他参数和观察数据的条件分布。
首先,我们评估表征基线表达分布(λgi)的参数(αg,βg)的条件分布。
这些参数使用Metropolis分别更新 -
黑斯廷斯算法。
对于潜状态zg和表达式
水平变化χg,首先提出状态zg,然后在给定状态的情况下采样χg。 Lewin等人。
[38]讨论了这种类型的移动与混合分布的各种选择。
关于(χg,zg)对的更新的详细信息在附录中描述。
混合比例(π0,π1)和混合分布的超参数
(σ20,σ21,μ1)从它们的条件后验分布中采样,后验分布可以以封闭形式导出。
DE分类和错误发现率估计
MCMC算法从所有模型参数的联合后验分布生成随机样本。
然后使用这些样本推断差异表达的状态。
一种选择一组有趣的方法
基因是使用估计的后均值折叠对基因进行排序
更改
χg≈exp
1T
Ť
t = 1时
日志
χ(t)的
G
,
(3)
其中T是老化期后用于推理的迭代次数,χ(t)g是采样值
对于吉布斯采样算法的迭代t的倍数变化。
选择DE基因的另一种方法是考虑潜在变量zg。
在MCMC迭代期间,
表达状态与倍数变化估计一起被采样。
这些MCMC样本可用于通过计算差异表达的采样状态的比例来近似差分表达的后验概率:
pg = P(zg = 1 |数据)≈1T
Ť
t = 1时
一世
Z(t)的
G
= 1
。
贝叶斯规则根据最大后验概率分配基因的表达状态。
另一种方法是,如果非空的后验概率大于阈值(pthres),则对基因进行分类:pg> pthres。
例如,一个选择是pthres = 0.5。
可以从后面估计错误发现率
概率[31]:
FDR = 1
(pg> pthres)
g:pg> pthres(1 - pg)
(4)
该方法在R中实现,可在以下位置获得
http://bioinformatics.med.yale.edu。
结果与讨论
模拟
基于模型假设的模拟
在模型假设下生成数据时,进行模拟的第一部分以检查所提出方法的性能。
对于10,000个基因和10个个体,我们模拟表达计数
根据等式1在治疗之前和之后。
库大小均匀地从7到1,8百万个采样,相对预期的基线表达式λgi是从形状为0.1和速率为1,000的Gamma分布中提取的。
为简单起见,我们考虑效果大小的双组分对数正态混合模型。
对于无效基因(90%),
对数标度效应从正态分布中采样,平均值为0,标准差为(σ0)0.1,
而对数效应是从正态分布中采样的,平均值(μ1)为1.5,标准差为
对于非空基因,(σ1)为0.5。
对于模拟研究,真实的库大小用于参数估计。
表1中的结果表明,所提出的方法很好地估计了模型参数。
后验概率截止值为0.5,算法识别更多
超过97%的真实DE基因,FDR约为1%。
图2显示了估计的倍数变化,显示了我们算法的良好性能。
基于经验数据的模拟
在模拟的第二部分中,我们假设在给定治疗之前和之后同时测量5,000个基因的表达丰度。
对于相对较大的样本,个体数量设定为10
情况(情况1和4),5对于介质(情况2和5),3对于相对较小的样本情况(情况3和6)。
每个库的大小从1.8到300万随机采样,以使模拟计数分布兼容
与真实的数据分布。受感染的RNA-seq数据集(数据部分,Qian F.等人详细信息)
用作预期的基线计数数据以模拟观察到的平均特异性分散。
首先,我们用5,000个基因指数进行取样以获得预期
基线表达。 表达式从所选的计数通过矩阵汇总指数,其中来自该数据矩阵的行对应于原始数据矩阵中的所选基因,并且列对应于个体。然后,计算相对表达式(λgi,i = 1,...,N,等式1)与总计数成比例
在每个样本中。
在5,000个基因中,前4,000个假设没有变化(zg = 0),它们的对数倍变化log(χg),
从正态分布中采样,均值为0,方差为4×10-4。
对于其余的非空基因,
我们考虑了以下两种情况。
经验设置(案例1,2,3)利用来自的标称倍数变化
未感染的数据集。
情况4,5和6考虑理论设置,其中对数缩放的倍数变化是从平均分布中得出的,其均值为零,方差为1。
我们进一步筛选出真实倍数变化小于1.4的非空基因。
每个病例重复100次。
我们将我们的方法与DESeq(版本1.8.3)的性能进行比较
[22]和edgeR(版本2.6.10)[21],两种广泛使用的RNA-seq数据方法,用于识别
差异表达的基因。
这些两个方法假设负二项分布来解释由于复制引起的方差。
DESeq使用平滑曲线
计算过度离散作为平均表达水平的函数。
选项'pooled-CR'用于
估计过度离散参数[44]。
在edgeR中,使用公共色散设置,其假设所有特征的一致过度色散,并使用公共似然函数估计参数。
通过利用广义线性模型可以合并成对设计。
对于每个应用,
真正的库大小用作库大小输入。
表2总结了我们的方法的结果。
总的来说,我们看到我们的方法在推断表达变化状态(反映在与真实状态的高度相关性)以及表征无效和非空基因的分布的参数方面的出色表现。
由于真实的表达状态在模拟中是已知的,
如果pg> pthres,我们称一个特征是差分表达的,并将估计的错误发现率与真值进行比较(图3)。
对于样本量较大且pthres增加的情况,估计FDR很好,而对于小样本量则略低估。
图4显示了在四种不同模拟设置下平均100次模拟的接收器操作特性。
对于每个设置,
将真阳性率与假阳性率作图。
通过对来自最大的基因进行排序来计算相应的比率
通过贝叶斯方法的后验概率(然后,最大倍数变化,如果并列)或者通过每种其他方法从最小的p值。
贝叶斯方法表明
在相同的假阳性率水平下比edgeR和DESeq具有更高的灵敏度。
特别是贝叶斯模型
对于较小的样本量和经验倍数变化设置(情况2或3),可以获得更好的性能。
我们进一步考虑了与真实数据类似的模拟场景。
如数据应用程序所示,
从数据估计的对数缩放倍数变化在零分量下具有较大的方差。
我们将空分量方差设置为0.35并重复模拟50次。
对于非空组中的特征,对数倍变化是从正态分布中采样的,平均值为-0.45,方差为4。
以10的样本大小(情况7)和大小5(情况8)进行模拟。
情况7和8的参数估计的平均值(μ1,σ20,σ21,π1)
分别为(-0.42,0.35,3.92,0.20)和(-0.42,0.35,3.85,0.21)。
与情况1至6类似,检查估计的错误发现率(图3),并将所提出的方法的性能与两种现有方法进行比较(图4)。
应用
贝叶斯模型的差分表达式分析
在本节中,我们将我们的方法应用于数据部分中描述的激励数据集。
模型参数的初始值直接从数据计算。
在丢弃前8,000次迭代后,MCMC采样运行4,000次迭代。
平均而言,每100次迭代计算时间约为5分钟。
通过监测MCMC样品的痕迹图确定总迭代次数和老化期(图5(a))。
我们估计混合比例
EE和DE组分别为0.88和0.12。
参数μ1和σ2的后验均值
1分别是-0.45和4.04。
空组的方差为0.35。
根据贝叶斯规则(pthres = 0.5),在西尼罗河病毒感染后,2,352个转录物被分类为DE。
公式4的估计FDR为16.2%。图5
(b)说明DE和DE下的倍数变化分布
EE基于贝叶斯规则分类。
估计的倍数变化在图6(a)中绘制
DE后验概率。
与现有方法进行比较
在这个部分,
我们比较了我们的方法和现有方法之间的DE分析结果。
DESeq或edgeR应用于相同的数据集,并且通过其p值选择前2,352个DE转录物。
edgeR与贝叶斯模型的一致性更高,为63.5%
重叠比DESeq有34.3%的重叠转录本。
具体来说,贝叶斯,edgeR和DESeq唯一地检测到832,632和1,364个转录本,
分别(图6)。
我们的方法检测到那些
低平均表达和高倍数变化。
相比之下,其他方法倾向于识别具有高表达水平和低倍数变化的更多转录物(图7)。
仅通过所提出的模型具有差异表达证据的转录物通常具有大的个体间变异。
除了一些低表达个体外,它们在治疗后的倍数变化很大。
图8显示了我们提出的方法的唯一标识的转录本的示例。
该转录物是SLAMF7的产物,已知SLAMF7在自然杀伤细胞活化中起作用
[45]。
所提出方法的另一个有趣特征是DE基因的比例在转录本长度上是一致的。
在最低10%的短记录中,4.6%通过提出的方法检测到,而2.4%通过其他方法检测到。
在长10%的长成绩单中,有6.5%被发现
所提出的方法,而DESeq和edgeR分别检测到7.4和8.9%。
要调查更多细节,
图9示出了当转录物基于其长度分成10个相等大小的箱时的DE比例。
生物信息学注释结果
途径水平分析是总结差异表达基因的生物相关性的一种有效方式。
我们使用DAVID(http://david.abcc.ncifcrf.gov/)进行基因富集分析。从我们的方法推断出的2,352 DE转录本被映射到1,518个DAVID ID以进行功能注释聚类。
簇1(DAVID富集得分:11.39)代表细胞反应
对WNV感染。
具体而言,集群中的路径
10(得分:2.72)与病毒感染后巨噬细胞的活化有关。
分子功能
这些转录物的特征在于它们在簇3中的细胞因子产生(GO:0001817)。
簇8(得分:2.89)由参与凋亡的转录物(GO:0042981)和程序性细胞死亡的调节(GO:0043067)组成。
细胞凋亡的诱导
WNV在促炎反应的调节中是必不可少的,并且先前已在细胞系中报道
和神经元细胞类型[46,47]。
这些聚类和相关的顶部途径在表3中报告,具有富集分数和p值。
结论
在本文中,我们提出了一种分层混合模型,用于鉴定西尼罗病毒驱动的RNA-Seq数据中的差异基因表达
研究,收集多个样本的样本,即每个人的治疗前和治疗后。
虽然这种设计在生物学研究中很常见,
现有的方法很少适当地分析这些数据
使用分层贝叶斯混合模型与推理相结合
通过MCMC,
我们的方法包含可变性
跨越基因,个体和治疗效果的背景
配对实验。
适用于两个模拟
和实际数据表明我们的模型和实现适用于配对设计,
与现有方法相比具有明显的优点。
模拟研究表明,我们的贝叶斯环境可以更好地检测差异基因表达。
在实际数据应用中,
我们提出能够识别具有大治疗效果但低表达水平的转录本,
而这些转录本并未被推断为通过其他方法差异表达。
这可能是由于我们的方法中个体之间的方差模型更灵活,适应性更强。
进一步检查这些排名靠前的特征
成绩单显示
短转录组中排名最高的转录本的比例与长转录组中的比例一致。
另一方面,通过现有方法检测的基因组
显示偏向更长的成绩单,
正如[48,49]之前的文献中所指出的那样。
我们的模型减少了这种偏差,因此有助于检测其他方法遗漏的一些短长度差异表达的转录本。
我们假设对数倍变化是由两个正态分布的混合产生的。
在DE下,模型允许对数倍变化分布的平均值不是
限制为零。
通过这样做,
我们提出的模型可以应用于显示过度表达和表达不足之间不对称的数据。
在经验倍数变化情景下,模拟研究表明正态分布假设是稳健的。
其他可能的选择
null基因包括0 [50]处的点质量,0附近的均匀分布,
和log-Gamma分布,平均值为0。
在双组分混合物设置下,可以对非空基因进行类似的分布假设。
或者,可以考虑三种组分的混合物
由等于,超过和表达不足的状态组成。
通过允许个体间表达变化幅度的变化,可以考虑进一步延伸。
附录
个人之间的差异
Poisson-Gamma设置(公式1和2)允许计数表达值之间的额外差异[28]。
计数的方差如下
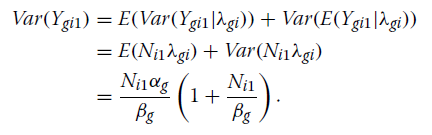
建模细节
zg和χg的关节密度为p(χg,zg)~π0LogNormal(0,σ20)I(zg = 0)+π1LogNormal(μ1,σ21)I(zg = 1)。设θ是所有模型参数的矢量,θ=({αg},{βg},π0,π1,σ20,μ1,σ2
1)。

这里,关于λgi积分的一些细节如下。
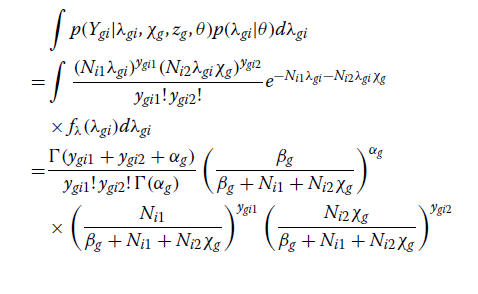
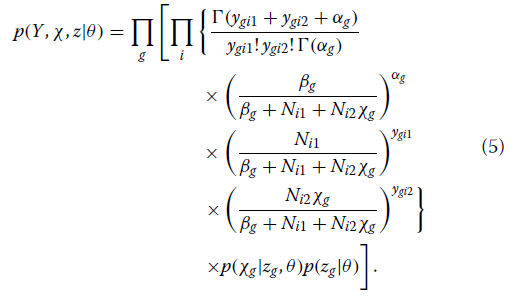
在整合了预期的基因和个体特异性相对基线表达(λgi)后,
未知参数的后密度与似然和先前密度的乘积成正比。
p(χ,z,θ| Y)αp(Y,χ,z |θ)p(θ)
我们对方法部分中指定的未知模型参数使用非信息性先验分布。

Metropolis-Hastings算法的参数估计
(MCMC)
我们使用吉布斯采样推断后验分布[43],迭代地从给定其他参数的每个参数的条件分布中对模型参数进行采样。
在本节中,我们将描述
后推理的程序。
步骤1
更新αg。
αg的条件分布没有闭合形式表达式。
我们使用Metropolis-Hastings算法对此参数进行采样。
更具体地说,我们通过提议来更新参数
α新
每次迭代时g~N(αoldg,σ2α),其中σα设定为0.1。
该提议以概率min {1,r}被接受,
其中r是接受率。




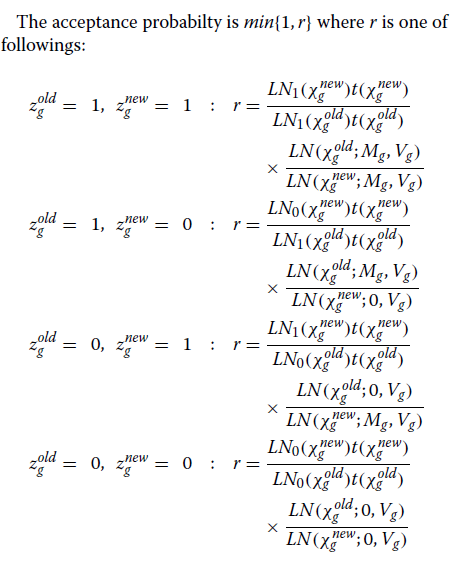

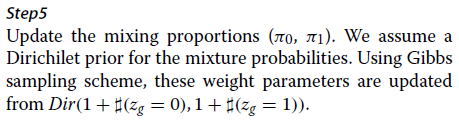
图1说明配对的RNA-Seq数据的分层模型。
图2估计的倍数变化。左侧面板显示了贝叶斯规则下EE和DE下估计倍数变化的分布。
红线是真正的倍数变化分布。右侧面板显示估计和真实倍数变化之间的关系。
表2经验模拟的估计后验平均值和结果
图3模拟的错误发现率。
在后验概率的不同阈值之间比较真实和估计的错误发现率。
实线是真值,虚线是在所有模拟中平均的估计值。
左侧面板显示模拟案例1,2和3的结果,其中根据经验生成非零倍数变化。案例4,5,6和7,8的结果分别在中间面板和右面板上示出。
图4模拟结果。 8个模拟设置的操作特性用红色,绿色和蓝色线绘制,用于Bayes,DESeq和
edgeR方法分别。
图5关于混合物分布的参数痕迹。通过贝叶斯规则(b)分别分析关于混合物分布的参数(a)和分类为EE和DE组的基因的倍数变化估计的分布。
图6贝叶斯方法的结果以及与其他现有方法的比较。
针对估计的倍数变化的后验概率
(a)当选择相同数量的顶级成绩单时,贝叶斯方法与现有方法之间的一致性(b)。
图7 DE转录本的比较。
通过所有三种方法共同检测的转录物用紫色标记:对数标度贝叶斯估计的倍数变化与对数标度平均表达。
其他三个图显示了通过三种方法中的每一种检测到的DE转录物。对于Bayes,DESeq和edgeR方法,它们分别用红色,绿色和蓝色标记。
表达
图8由提出的贝叶斯模型唯一选择的示例。表达式中的expresseion值的插图
仅提出方法。
图9 DE比例和转录本长度。 DE转录本在其平均表达水平上的比例。转录本按其表达水平划分为10个相等大小的区域。
推断为DE的转录物的比例绘制在y轴上。
红色,绿色和蓝色线来自Bayes,DESeq和edgeR
方法,分别。
利益争夺
作者声明他们没有竞争利益。
作者的贡献
LMC开发并实施了所提出的模型,进行了统计
分析,并起草了手稿。 JPF参与了模型开发并帮助准备了稿件。 WZ处理了WNV数据并参与了数据分析。 FQ,VB和RRM进行了WNV实验。
HZ设计并协调了研究,并帮助起草了手稿。
所有作者阅读并认可的终稿。
致谢
这项工作部分由NIH的Grant GM59507支持,
来自PHS / DHHS的5T15LM007056-25,来自耶鲁CTSA拨款的UL1 RR024139,
和NIH颁发的奖项(HHS N272201100019C,AI 070343,AI 089992)。
作者详情
1耶鲁大学公共卫生学院生物统计学系,纽黑文,
美国康涅狄格州。 2乔治华盛顿大学统计系,
华盛顿特区,美国。 3Novartis剑桥生物医学研究所,
美国马萨诸塞州。 4美国康涅狄格州纽黑文耶鲁大学医学院风湿病科。马里兰大学巴尔的摩分校5微生物学和免疫学系,
美国。收稿日期:2012年10月16日接受日期:2013年3月1日
发布时间:2013年3月27日