[论文阅读笔记] LouvainNE: Hierarchical Louvain Method for High Quality and Scalable Network Embedding
本文结构
- 解决问题
- 主要贡献
- 算法原理
- 参考文献
(1) 解决问题
本篇论文是针对现有表征算法计算开销比较大,不能够很好应用到大规模网络上的问题。
(2) 主要贡献
Contribution: 提出一种快速且可扩展网络表征框架,LouvainNE,能够为包含数百亿边的网络生成高质量的表征向量。
(3) 算法原理
LouvainNE的算法思想也就是基于粗化图的,与HARP类似,但是粗化方式不同,粗化图的使用方式也不同。
LouvainNE算法包含三个部分:
(1)类似自顶向下的层次聚类算法,构建层次子图(2)为每个层次子图中的节点生成特定节点表征,提出两个不同的方法来生成节点嵌入(标准嵌入和随机嵌入方法)(3)结合各个层次子图中节点获得的表征成最终节点表征。
-
自顶向下构建层次子图:使用Louvain算法生成的社区构成节点来进行划分。(满足一个假设,相似的数据节点应该在二叉树上的位置更接近)如下图所示:
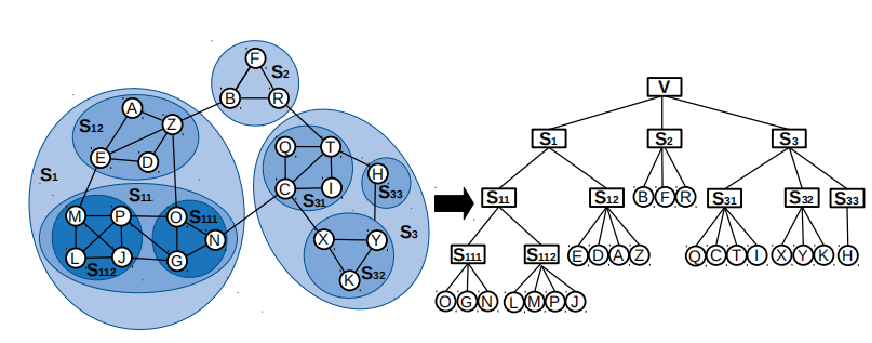
首先,使用Louvain算法得到原始图(对应上图树的根节点)的初始社区划分S1、S2、S3,每个社区可以看成一个粗化节点(对应上图中右半部分根节点的第一个分叉)。紧接着对S1、S2、S3分别递归使用Louvain再进行社区划分,分别得到各自的儿子节点,如上图中右边树所示,S1进一步划分为社区S11和S12。以上过程对树中每个非叶节点(粗化节点包含两个或多个原始图节点的为非叶节点,否则为叶节点)分别做,直到得到的儿子节点均只包含单个原始图中的节点,自顶向下层次子图构建完毕(每一层所有节点看成一个层次(粗化)图)。 -
为每个层次图中的节点学习表示向量(同一深度的节点位于同一层图中),提出标准嵌入方法和随机嵌入方法。
标准嵌入:使用其他表示学习算法来学习,如DeepWalk、Line、Node2vec等等,通常其他表示学习算法的输入需要图结构的,因此需要定义层次子图,点由每一层节点组成,节点之间的边由以下公式确定(ES1S2代表节点集合S1和S2之间存在的边):
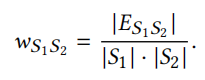
随机嵌入:使用标准正态分布随机生树中每个节点的表示向量,这种方法不需要构建图结构。(论文实验中对比了标准嵌入和随机嵌入的实验效果,emmm,结论是相差不大,考虑到随机嵌入效率比标准嵌入快很多,因为综合考虑还是使用随机嵌入的方法好。)
-
融合各层节点表示生成节点最终表示向量,我们只要得到树中所有叶节点的表示向量即课得到原始图的表示向量:我们可以发现,从根节点到叶节点对应唯一路径,聚合路径中节点的向量表示(结合各个层的表示,从而融合局部到全局的结构特征)即可得到叶节点的向量表示(即路径上其他节点向量的线性组合)。聚合方式如下所示(越靠近根节点的节点的向量表示越重要,h为树的深度,α为超参数(属于[0,1],衡量当前深度的节点表示向量对叶子节点表示向量的重要性),ytv为在第t深度的路径中节点的表示向量):

以上便是LouvainNE算法的全部内容,通过Louvain算法获取社区信息,将社区构造为粗化节点,逐级递归,构造层次树,最后结合叶节点对应的路径上所有粗化点的表示得到叶节点的表示。
(4) 参考文献
Bhowmick A K, Meneni K, Danisch M, et al. LouvainNE: Hierarchical Louvain Method for High Quality and Scalable Network Embedding [C] // Proceedings of the 13th International Conference on Web Search and Data Mining. 2020: 43-51.