85.最大矩形

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例:

输入:
[
["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]
]
输出: 6

解:

这题参考了一个答案的解法，自己又写了一遍

参考这里，遍历每个点，求以这个点为矩阵右下角的所有矩阵面积。如下图的两个例子，橙色是当前遍历的点，然后虚线框圈出的矩阵是其中一个矩阵。

怎么找出这样的矩阵呢？如下图，如果我们知道了以这个点结尾的连续 1 的个数的话，问题就变得简单了。

 

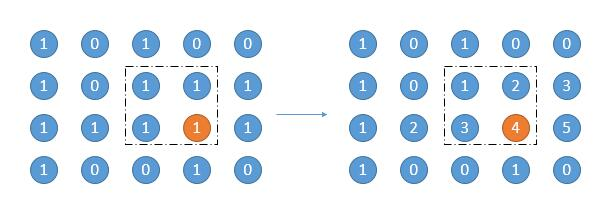
首先求出高度是 1 的矩形面积，也就是它自身的数，如图中橙色的 4，面积就是 4。

然后向上扩展一行，高度增加一，选出当前列最小的数字，作为矩阵的宽，求出面积，对应上图的矩形框。

然后继续向上扩展，重复步骤 2。

按照上边的方法，遍历所有的点，求出所有的矩阵就可以了。

以橙色的点为右下角，高度为 1。

 

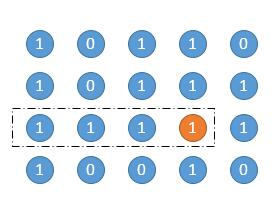
高度为 2。

 

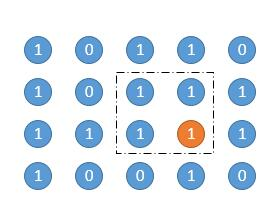
高度为 3。

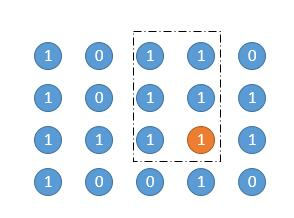
作者的java代码，自己写的比较挫就不放上来了

public int maximalRectangle(char[][] matrix) {
    if (matrix.length == 0) {
        return 0;
    }
    //保存以当前数字结尾的连续 1 的个数
    int[][] width = new int[matrix.length][matrix[0].length];
    int maxArea = 0;
    //遍历每一行
    for (int row = 0; row < matrix.length; row++) {
        for (int col = 0; col < matrix[0].length; col++) {
            //更新 width
            if (matrix[row][col] == '1') {
                if (col == 0) {
                    width[row][col] = 1;
                } else {
                    width[row][col] = width[row][col - 1] + 1;
                }
            } else {
                width[row][col] = 0;
            }
            //记录所有行中最小的数
            int minWidth = width[row][col];
            //向上扩展行
            for (int up_row = row; up_row >= 0; up_row--) {
                int height = row - up_row + 1;
                //找最小的数作为矩阵的宽
                minWidth = Math.min(minWidth, width[up_row][col]);
                //更新面积
                maxArea = Math.max(maxArea, height * minWidth);
            }
        }
    }
    return maxArea;
}