题目描述:
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
方法一: 回溯 + 剪枝
将 生成 n 对 有效括号的过程就是在一棵剪枝了的二叉树上遍历的过程。下图是 n = 3 的情况。
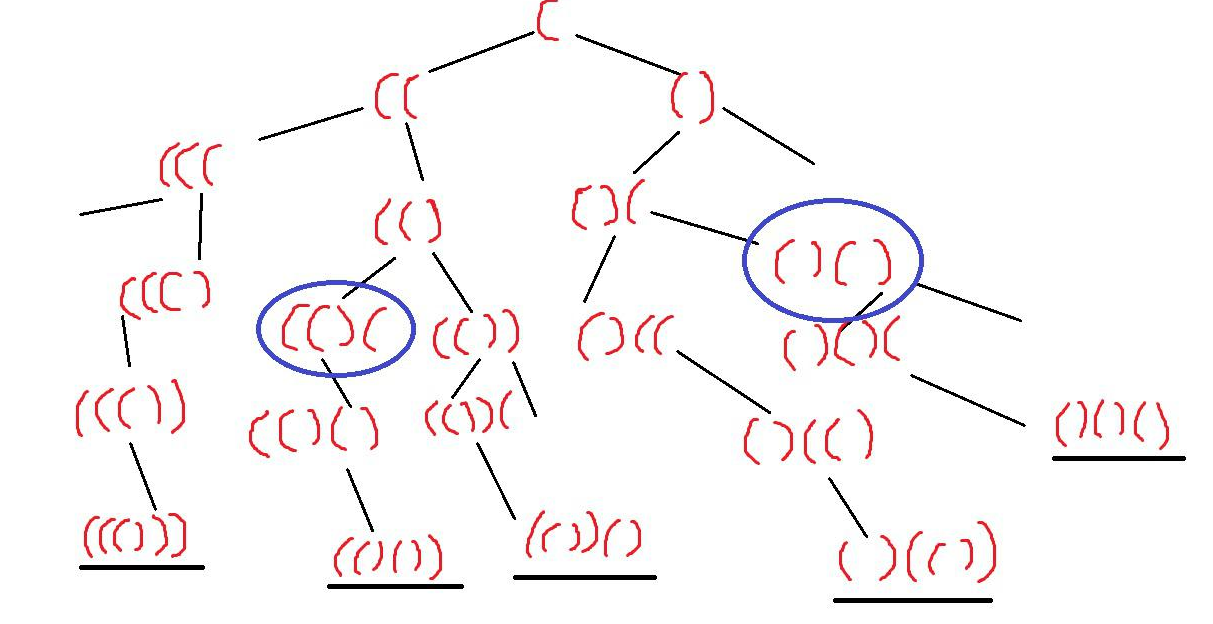
从上面的图片中我们可以很明显的看到,最后五条画黑线的叶节点就是最终的结果,其中左分支都是添加左括号,
右分支都是添加右括号。
添加左(右)括号的条件是 当前还有 左(右)括号可以用,特别地,添加右括号还需要当前 已经添加的右括号的数量
不能比已经添加的左括号的多。因为 合法的括号序列的第一个一定是左括号,此时右括号数量要是比左括号多,那一定有右括号
还没有左括号配对。
所以,剪枝条件 就是 if (l > n || r > n || r > l) { return } 。l ,r 分别表示当前状态下,序列中 左右括号的数量。初始化为 0;
如上图,遍历到黑线叶节点,即得到 了一个合法的 括号序列,需要将得到的合法序列 放到结果集中。
代码如下:
class Solution {
public:
vector<string> generateParenthesis(int n)
{
N = n;
res.clear();
dfs("",0,0);
return res;
}
void dfs(string str,int l,int r)
{
if(l > N || r > N || r > l)
{
return;
}
if(l == N && r == N)
{
res.push_back(str);
return;
}
dfs(str + '(', l + 1, r);
dfs(str + ')', l, r + 1);
return;
}
private:
vector<string> res;
int N;
};
方法二: 动态规划
分析:动态规划的问题可以使用类似于数学归纳法的思想来分析,假设我们已经知道了 0,1,2,... ,n-1 对括号的所有的合法括号序列,
现在 求 有 n 对括号的所有的合法序列。对 一个 有 n 对 括号的 合法括号序列,一定是 '(' 开头的 。
合法括号序列的 形式为 "(" + in_str +")" + out_str ,且 in_str 和 out_str 都是合法的括号序列串或空串。
假设 "(" + in_str +")" + out_str 是一个有n 对 括号的 合法括号序列,假设 in_str 有 n1 对括号,out_str 有n2 对括号。
n 1 和 n2 之间必须满足:
0 <= n1 <= n-1 , 0 <= n2 <= n-1 , n1 + n2 = n - 1
假设 n = 3 ,则有
n1 n2
0 2
1 1
2 0
所以,求 有n 对 括号的所有的合法括号序列,即求上面 n_str 和 out_str 的所有组合情况。
另 vector<vector<string> > dp(n+1); dp[i] 表示 有i 对 括号的 所有合法序列,设 0<= j <= i-1 ,则 in_str 是 dp[ j ]中的一个序列,
同时 out_str 是 dp[i-1 -j] 中的一个序列。
c++ 代码如下:
1 class Solution { 2 public: 3 vector<string> generateParenthesis(int n) { 4 vector<vector<string> > dp(n+1); 5 if( n <= 0) return {}; 6 //base case 7 dp[0] = {""}; 8 dp[1] = {"()"}; 9 //dp status move 10 for(int i = 2; i <= n;++i) 11 { 12 for(int j = 0;j <= i-1 ; ++j) 13 { 14 for(string &in_str:dp[j]) 15 for(string &out_str:dp[i-1-j]) 16 { 17 string str_tmp = "(" + in_str + ")" + out_str; 18 dp[i].push_back(str_tmp); 19 } 20 } 21 } 22 return dp[n]; 23 } 24 };