10-4 国庆节第七场模拟赛题解
T1工厂 (factory)
水
#include<iostream>
#include<cstdio>
#define int long long
using namespace std;
inline int read(){
int sum=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
sum=(sum<<1)+(sum<<3)+ch-'0';
ch=getchar();
}
return sum*f;
}
const int wx=10017;
int n,s,ans;
int f[wx],a[wx],c[wx];
signed main(){
freopen("factory.in","r",stdin);
freopen("factory.out","w",stdout);
n=read();s=read();
for(int i=1;i<=n;i++){
c[i]=read();a[i]=read();
}
f[1]=c[1];
ans+=(f[1]*a[1]);
for(int i=2;i<=n;i++){
f[i]=min(f[i-1]+s,c[i]);
ans+=(f[i]*a[i]);
}
printf("%lld
",ans);
fclose(stdin);
fclose(stdout);
return 0;
}
T2铁路 (trainfair)
Description
在 MS 国有 N 座城市,编号从 1 到 N ,其中 1 号城市是 MS 国的首都。
MS 国里,只有一家铁路公司,经营着 M 条连接着各城市的铁路线路,每条线路都双向地连接着两座不同的城市。通过这些线路,我们可以在任意两座城市间通行。
原本,乘坐一条线路只需要花费 1 角钱。可是由于经营不善,铁路公司提出计划,要在今后的 Q 年间,每年给某一条线路涨价为 2 角钱。保证一条线路不会被涨价多次。
另外,这个铁路公司每年都会在每一座城市进行一次居民满意度调查。原本每一座城市中的居民都对铁路公司的服务十分满意,但在线路涨价后就说不定了。每一年的满意度调查都会在当年的涨价计划实施后进行。如果一座城市中的居民在当年坐火车去首都所需的最少花费相比于计划提出前增加了,他们就会对铁路公司抱有不满。首都的居民永远不会对铁路公司抱有不满。
在计划施行前,你需要帮助铁路公司统计出未来的每一年中,各将有多少城市的居民对铁路公司抱有不满。
Input
输入文件第一行包含三个正整数 N, M, Q,分别表示 MS 国的城市数量、铁路路线数量和涨价计划将要实施的时间长度。
接下来 M 行,其中第 i行包含 22 个整数 Ui,Vi,表示第 ii 条路线连接着编号为 Ui 和 Vi 的两座城市。
接下来 Q 行,其中第j 行包含一个整数 Rj,表示计划施行后第 j 年将会让第 Rj 条线路涨价。
Output
输出 Q 行,其中第 j 行表示第 j 年居民对铁路公司抱有不满的城市的数量。
最短路拥有一个性质:
对于x与y之间的一条边设为z,那么如果dis[x]=dis[y]+edge[z].dis或者dis[y]=dis[x]+edge[z].dis,那么我们就将这种边单独挑出,那么所有满足这种情况的边所组成的图是一个拓扑图。
针对这个性质搞事情,分析一下这道题,将边权从一角长为两角其实就相当于把这条边删去。因为他对后面的点的到点1的最短路的改变的情况和删去是等价的。
那么我们就可以把所有满足上述性质的边拿出来建出一个拓扑图。
为什么要把这些边拿出来呢?
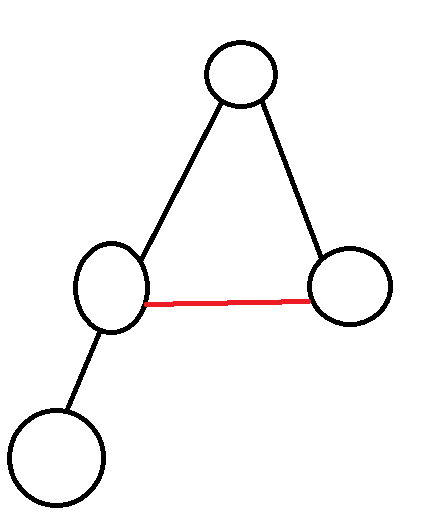
对于上图的红色边,显然他并不是符合上述性质的边,即不是最短路上的边,那么如果这条边变化了,对任何的点都不会有任何影响。
换一种角度来说,每一个点和一的最短路,都只会因为从一到这个点的最短路上的边的改变而改变,所以做法就很明了了。
把所有的最短路上的边拿出组成一个拓扑图,开始输入每一条要删掉的边,去找这条边的两个端点中距离1更远的点,那么在判断完这条边是最短路上的边上后,我们就可以把这个点的入度减一了,同时把这条边的标记清零。
那么如果这个点的入度减为了零,那么就说明这个点没有办法从其他的路径走最短路到1了,所以这时的全局增量ans就可以加一了。
我们又可以想到,如果删除了这个点,那么肯定会影响到后面的点,所以我们就要从这一个点开始向后延伸,也就是把这个点所有的出边全部删去,在判断会不会有新的点的入度变为0,使得ans++,再继续向下。
因为每个点只能被删一次,所以复杂度:O(n)
code:
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int wx=200017;
inline int read(){
int sum=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
sum=(sum<<1)+(sum<<3)+ch-'0';
ch=getchar();
}
return sum*f;
}
struct e{
int nxt,to,dis,flag,he;
}edge[wx*2];
int head[wx],dep[wx],in[wx],vis[wx];
int num,n,m,q,ans,x,y,z;
void add(int from,int to,int dis){
edge[++num].nxt=head[from];
edge[num].to=to;
edge[num].he=from;
edge[num].dis=dis;
head[from]=num;
}
queue<int > qq;
void Dij(int u){
for(int i=1;i<=n;i++)dep[i]=2147483642,vis[i]=0;
dep[1]=1;qq.push(1);vis[1]=1;
while(qq.size()){
int u=qq.front();qq.pop();
vis[u]=0;
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(dep[v]>dep[u]+edge[i].dis){
dep[v]=dep[u]+edge[i].dis;
if(!vis[v]){
vis[v]=1;
qq.push(v);
}
}
}
}
}
void mark(){
for(int u=1;u<=n;u++){
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(dep[u]>dep[v])continue;
if(dep[u]==dep[v]-1){
edge[i].flag=1;in[v]++;
}
}
}
}
int find(int now){
int re=0;
for(int i=head[now];i;i=edge[i].nxt){
if(!edge[i].flag)continue;
int v=edge[i].to;if(!in[v])continue;
if(dep[v]<dep[now])continue;
in[v]--;edge[i].flag=0;
if(!in[v])re+=find(v)+1;
}
return re;
}
int main(){
freopen("trainfair.in","r",stdin);
freopen("trainfair.out","w",stdout);
n=read();m=read();q=read();
for(int i=1;i<=m;i++){
x=read();y=read();add(x,y,1);add(y,x,1);
}
Dij(1);
mark();
for(int i=1;i<=q;i++){
x=read();
if(dep[edge[x*2].he]<=dep[edge[x*2].to]&&edge[x*2].flag){
x*=2;
int now=edge[x].to;if(!in[now])goto zz;
in[now]--;edge[x].flag=0;
if(!in[now])ans+=find(now)+1;
}
else if(dep[edge[x*2-1].he]<=dep[edge[x*2-1].to]&&edge[x*2-1].flag){
x=x*2-1;
int now=edge[x].to;if(!in[now])goto zz;
in[now]--;edge[x].flag=0;
if(!in[now])ans+=find(now)+1;
}
zz:;
printf("%d
",ans);
}
return 0;
}
T3 数学题 (math)
Description
给定一个长度为 n 的序列 a,请你算一算这个式子:
(sumlimits_{i=1}^nsumlimits_{j=i}^n(j-i+1)min(a_i,a_{i+1},dots,a_{j})max(a_i,a_{i+1},dots,a_{j})).
由于高精度写起来太麻烦了,请将答案对 10^9109 取模后输出。
Input
- 输入文件第一行包含两个数字 n, 表示序列 a 的长度。
- 接下来一行包含 n 个数字,依次表示序列中的元素a1,a2,...,an。
Output
输出式子的值对 (10^9) 取模后的结果。
对于这道题:每一次把区间分成等长的两个小区间。每一次不考虑被包括在当前区间的左区间或者右区间的小区间的答案,只考虑l和r跨过当前大区间的mid的小区间的答案。因为这个时候不求的话,按照我们的求解策略,这个区间下一次一定会被分开,那么就导致一部分答案被忽略了。
那么主要任务就是给你一个区间:
左端点的范围是l到mid,右端点的范围是mid+1到r
所以求解答案为:
考虑枚举所求区间的左端点。
cdq分治的思想有一部分就是对于求取答案,我们必须通过比较暴力的方式去求去出一些有用的信息。为了方便,把这个区间分成左右两个区间,然后我们在左区间去找有效信息,再对应到右区间去实现更新答案,这也是为什么只会在当前区间计算跨过mid的区间的答案。
所以对于这道题,我们枚举小区间的左端点,那么可以在枚举的过程中确定从i到mid的最大值和最小值记为maxl和minl,那么为了左区间有效信息充分利用的原则,我们就要考虑右端点j在什么范围可以使得这两个量可以被利用到。
那就开始分析吧:
现在我们有两个量maxl和minl,他们都会有两个状态,就是可以被用和不可以被用。
那么就有三种情况:一是两者都可以用,二是两者只有一者可以用,三是两者都不可以用。
并且我们已知maxl和minl确切的值,并且在我们从mid向前枚举i的时候,当前的maxl和minl都是后缀最值,所以是具有单调性的。
同样的,我们设A作为一个下标满足:(a[A]<=maxl &&a[A+1]>maxl)
设B作为一个下标满足:(a[B]>=minl&&a[B+1]<minl)
那么通过A和B就可以确定maxl和minl在哪个范围起作用。
所以现在的任务就是找到A和B。
因为A,B的权值是前缀极值,并且我们从前向后找,所以是满足单调性的,完全可以二分找一下。
不过这里我偷了一下懒直接暴力找的A,B,(好吧其实我不会。。。),也是可以的。
找到A,B之后,我们就会发现A和B将mid到r这段区间分成了三段对应了maxl和minl的适用范围。
这里我们假设A<B;

那么现在对这三段进行分析。
一,当(mid+1leq j&&j leq A),这个时候区间i到j的最大值和最小值就是maxl和minl,所以就可以写出答案公式:
二,当(A+1 leq j&&jleq B),这个时候区间i到j的最大值就不会是maxl了,因为这就是A的定义。但是minl还是可以作为区间最小值的。
所以当我们找到一个对应的j的时候,就需要一个到j的前缀最大值。公式:
可以很清晰的看到我们只要维护好前缀和就可以O(1)得来求这部分的答案了。
另外,我们当前讨论的是A<B,那么对于B<A的情况也是要考虑的,判断一下就好,思路一致。
三,当(B+1 leq j &&jleq r)时,这个时候区间i,j的最大值和最小值就都不是maxl和minl了,那么仿照二的想法,也是很容易想出公式的。
在分别维护前缀和就好了。
注意边界,注意初始化,注意取模,这道题真的很好,但是真的恶心。
code:
#include<iostream>
#include<cstdio>
#define int long long
using namespace std;
const int mod=1e9;
inline int read(){
int sum=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
sum=(sum<<1)+(sum<<3)+ch-'0';
ch=getchar();
}
return sum*f;
}
const int wx=1000017;
int a[wx];
int s[wx],smx[wx],smn[wx],ss[wx],ssl[wx],smxl[wx],smnl[wx],mx[wx],mn[wx];
int n,ans;
void work(int l,int r){
if(l==r){
ans=(ans+(a[l]*a[r])%mod)%mod;return;
}
int mid=l+r>>1;
work(l,mid);work(mid+1,r);
mn[mid]=0x3f3f3f3f;
s[mid]=smx[mid]=smn[mid]=mx[mid]=ss[mid]=ssl[mid]=smxl[mid]=smnl[mid]=0;
for(int i=mid+1;i<=r;i++){
mx[i]=max(mx[i-1],a[i]);//f[i]存前缀最小值
mn[i]=min(mn[i-1],a[i]);//g[i]存前缀最大值
s[i]=(s[i-1]+i-mid)%mod;
ss[i]=(ss[i-1]+mn[i]*mx[i])%mod;
smx[i]=(smx[i-1]+mx[i])%mod;
smn[i]=(smn[i-1]+mn[i])%mod;
ssl[i]=(ssl[i-1]+mx[i]*mn[i]%mod*(i-mid))%mod;
smxl[i]=(smxl[i-1]+mx[i]*(i-mid))%mod;
smnl[i]=(smnl[i-1]+mn[i]*(i-mid))%mod;
}
int A=mid,B=mid;
int maxl=0,minl=0x3f3f3f3f;
for(int i=mid;i>=l;i--){
maxl=max(maxl,a[i]);
minl=min(minl,a[i]);
while(B<r&&mx[B+1]<maxl)B++;//B维护最后一个小于等于Max的位置;
while(A<r&&mn[A+1]>minl)A++;//A维护最后一个大于等于Min的位置;
// if(A<=B){
// ans=(ans+maxl*minl%mod*((mid-i)*(A-mid+1)+(mid-i)*(mid-i-1)/2)%mod)%mod;
// ans=(ans+maxl*(sumff[B]-(i-1)*sumf[B])%mod-maxl*(sumff[A-1]-(i-1)*sumf[A-1])%mod)%mod;
// ans=(ans+(Sum[B]-(i-1)*SUm[B])-(Sum[A-1]-(i-1)*SUm[A-1]))%mod;
// }
// else {
// ans=(ans+maxl*minl%mod*((mid-i)*(B-mid+1)+(mid-i)*(mid-i-1)/2))%mod;
// ans=(ans+minl*(sumgg[A]-(i-1)*sumg[A])%mod-minl*(sumgg[B-1]-(i-1)*sumg[B-1])%mod)%mod;
// ans=(ans+(Sum[A]-(i-1)*SUm[A])-(Sum[B-1]-(i-1)*SUm[B-1]))%mod;
// }
int x=min(A,B),y=max(A,B);
int ii=mid-i+1;
ans=(ans+(s[x]+ii*(x-mid))*maxl%mod*minl)%mod;
if(B<=A)
ans=(ans+(smxl[y]-smxl[x]+ii*(smx[y]-smx[x]))%mod*minl)%mod;
else
ans=(ans+(smnl[y]-smnl[x]+ii*(smn[y]-smn[x]))%mod*maxl)%mod;
ans=(ans+(ssl[r]-ssl[y]+ii*(ss[r]-ss[y])))%mod;
}
}
signed main(){
freopen("math.in","r",stdin);
freopen("math.out","w",stdout);
n=read();
for(int i=1;i<=n;i++)a[i]=read();
work(1,n);
printf("%lld
",(ans+mod)%mod);
return 0;
}