在上次的分享中,介绍了模型建立与使用梯度下降法优化参数、梯度校验,以及一些超参数的经验。
本节课的主要内容:
1==链式法则
2==深度学习框架中链式法则
3==全连接神经网络
=========================================================================================
1、链式法则
目前我们所处的阶段:

学习了SVM softmax两个模型或者算法,需要优化w》》梯度下降。
上述公式的计算图例:

由上述计算图可见,模型非常简洁,可以使用计算偏导的方式来优化参数,但是当模型非常大时,比如:


此时直接求偏导的方法不可行。
解决方法》》链式法则。
举例:
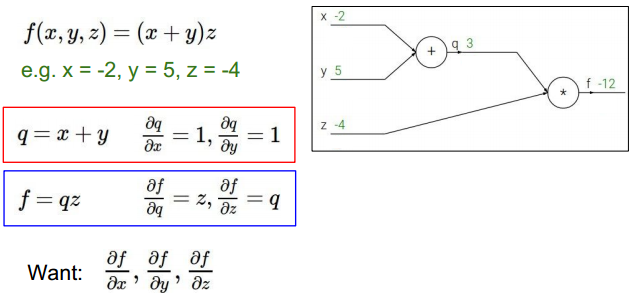
对具体函数用链式法则求导。首先进行前向计算。如上图。
求f对中间变量偏导:

求中间变量对初始变量的偏导,结合之前计算,得到f对初始变量的偏导》》链式法则
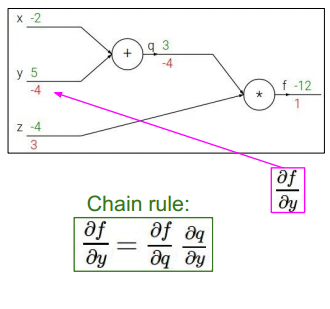

链式法则解释:
单一结点,输出值对输入变量的偏导:
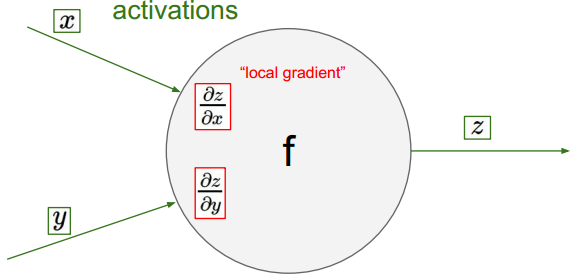
计算此结点与下一节点,联合对输入变量的偏导:

多节点:
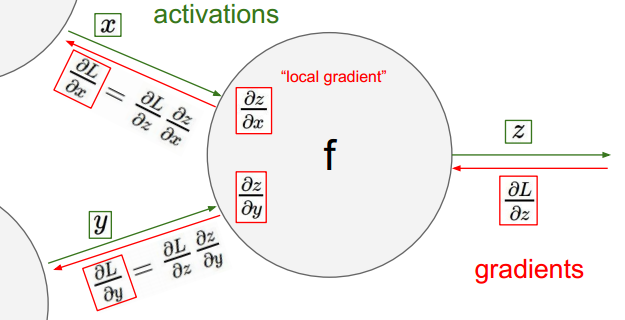
上述即为链式法则的过程。
实际例子:

可视化流程如上,其中已经实现了前向计算。
反向传播,首先计算最后节点:

倒数第二个节点:

按照上述方法,逐一反向计算:
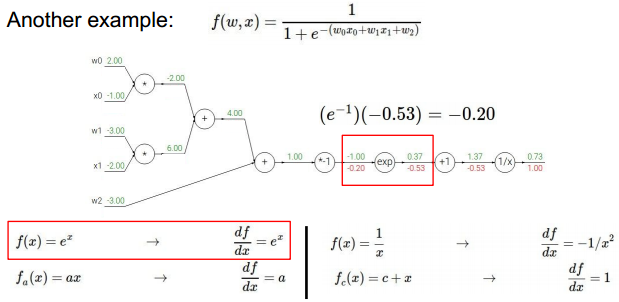

达到分支时:


可以对某些步骤进行简化》》直接对某个表达式整体求导:
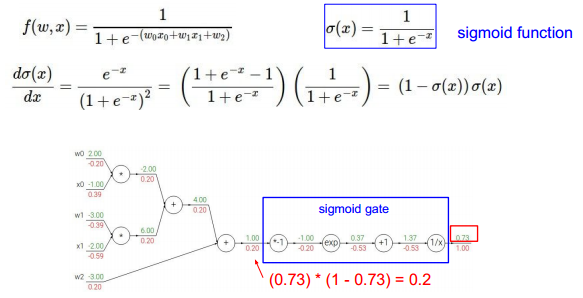
各种计算的链式计算以及代码结构:
加法:


乘法:

深度学习框架实现:


向量形式的链式法则:
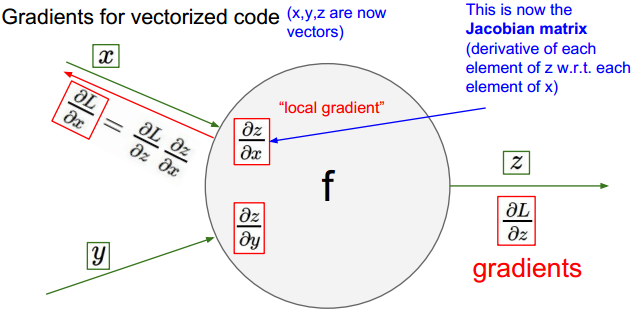
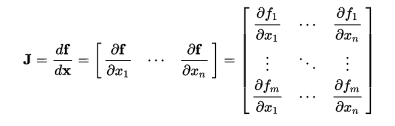
向量形式链式法则举例:
问题:
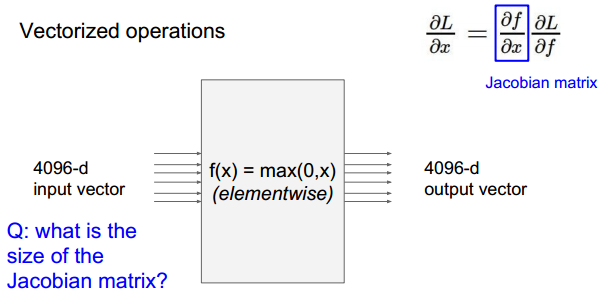
问题:
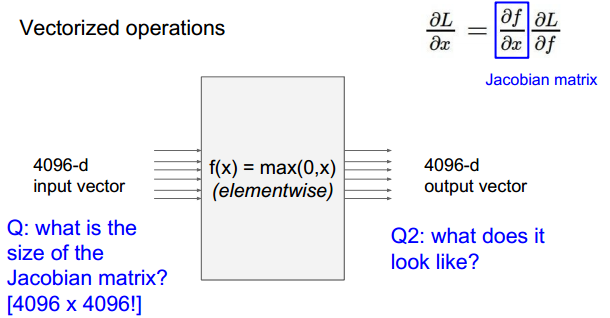
此时的输出如f1只与x1相关,所以对应的雅克比行列式只有在对角线上有值,为0或者1.其余元素均为0.
由此可见,计算雅克比矩阵的方式不是很简洁。
总结:

=========================================================================================
2、神经网络 Neural Network
两层NN与线性函数对比:

之前的分类器得到的可视化:

可视化的结果显示,模型将某一类的特征训练调整到单一的w(向量或矩阵),此时的w混合了很多特点,比如颜色、形状。
而NN包含了很多隐藏层,隐藏层的某个节点对应相应的某个特征,比如颜色,方向等等。将隐藏层节点得到的特征抽象到输出,可以得出结果。
两层隐藏层:

代码实现:

其实就是层的叠加。
前向、反向传播代码结构:

具体细节在下一节课会涉及。
NN的生物学知识:
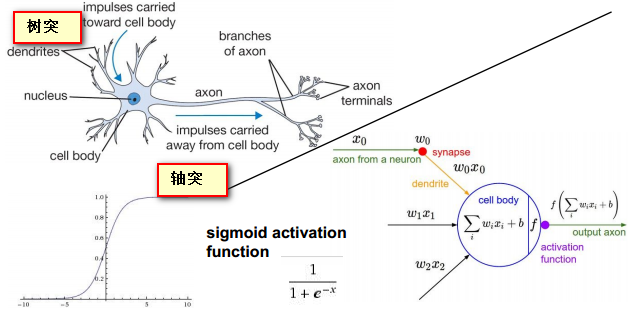
使用sigmoid作为激活函数。
神经系统中的树突如输入层到隐藏层节点的连接。轴突相当于隐藏层节点的输出与其他节点的连接。
代码实现(结构):
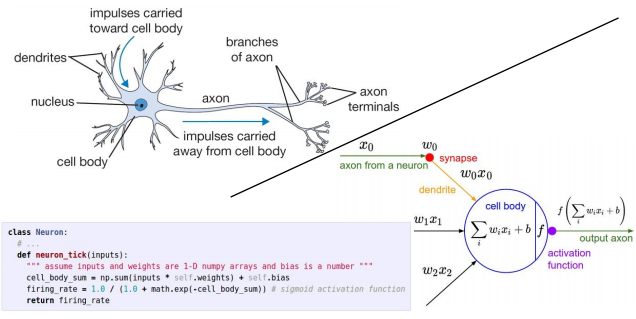
一些区别:

生物神经系统功能更复杂。
常用的激活函数:
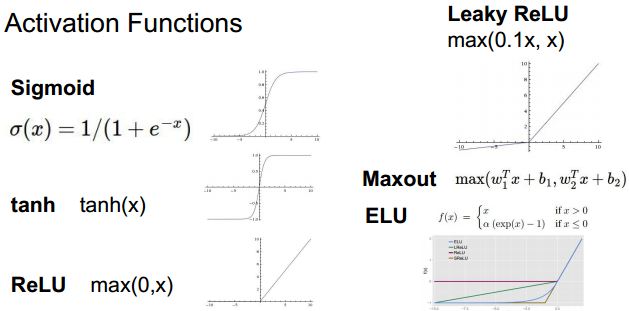
根据模型特点以及计算的效果,选择不同的激活函数。其中ReLU、Maxout比较常用。
各个激活函数的特点在课程配套的笔记中有详细说明。之后会把总结好的笔记扫描、分享出来。
NN层数:
下图以2 3层网络为例,层数不计输入层,注意与UFLDL进行对比,UFLDL中计入了输入层:

前向传播代码结构:

前向传播实例:
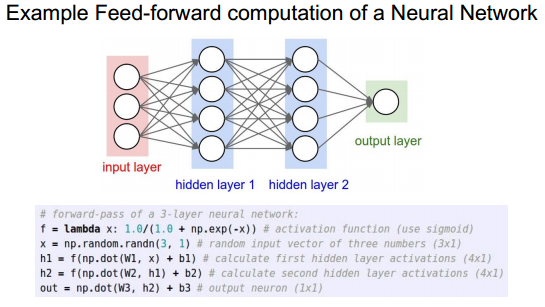
关于NN的层数:
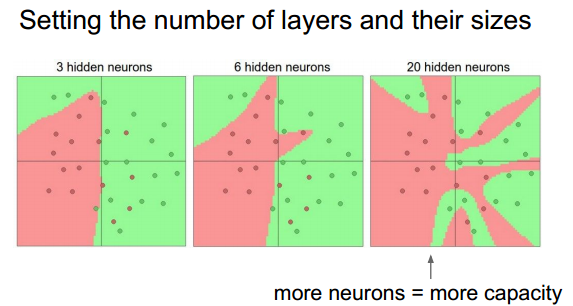
NN可以视为对飞线性函数的逼近》》证明可以逼近任何函数。
由上图可见,NN层数不同,分类的准确率也有差异,一般选取3层或以上的层数,并加入正则的方式。
当高于3层时,层数的增加并不能很好的改善最终的结果,甚至会产生过拟合。
cnn中层数较高表示抽象能力更强,希望较高的层数。
正则化强度对结果的影响:

可以通过选择合适的正则化强度系数控制过拟合结果。上图中看出较高的正则化强度系数使得分类界面更平滑。
=========================================================================================
总结:

下节课的内容:

附:通关CS231n企鹅群:578975100 validation:DL-CS231n