实验名称:贝叶斯分类器
一、实验目的和要求
目的:
掌握利用贝叶斯公式进行设计分类器的方法。
要求:
分别做出协方差相同和不同两种情况下的判别分类边界。
二、实验环境、内容和方法
环境:windows 7,matlab R2010a
内容:根据贝叶斯公式,给出在类条件概率密度为正态分布时具体的判别函数表达式,用此判别函数设计分类器。数据随机生成,比如生成两类样本,每个样本有两个特征,每类有若干个(比如20个)样本点,假设每类样本点服从二维正态分布,随机生成具体数据,然后估计每类的均值与协方差,在两类协方差相同的情况下求出分类边界。先验概率自己给定,比如都为0.5。如果可能,画出在两类协方差不相同的情况下的分类边界。画出图形。
三、实验基本原理
条件概率:
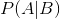 表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为:
表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为: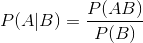 。
。
贝叶斯定理之所以有用,是因为我们在生活中经常遇到这种情况:我们可以很容易直接得出P(A|B),P(B|A)则很难直接得出,但我们更关心P(B|A),贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。
下面不加证明地直接给出贝叶斯定理:
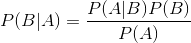
朴素贝叶斯分类是一种十分简单的分类算法,叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素,朴素贝叶斯的思想基础是这样的:对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。朴素贝叶斯分类的正式定义如下:
1、设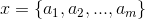 为一个待分类项,而每个a为x的一个特征属性。
为一个待分类项,而每个a为x的一个特征属性。
2、有类别集合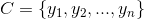 。
。
3、计算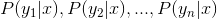 。
。
4、如果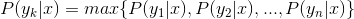 ,则
,则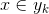 。
。
那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做:
1、找到一个已知分类的待分类项集合,这个集合叫做训练样本集。
2、统计得到在各类别下各个特征属性的条件概率估计。即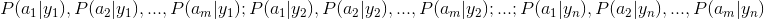 。
。
3、如果各个特征属性是条件独立的,则根据贝叶斯定理有如下推导:
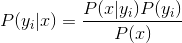
因为分母对于所有类别为常数,因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的,所以有:
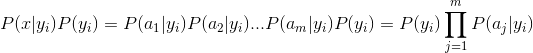
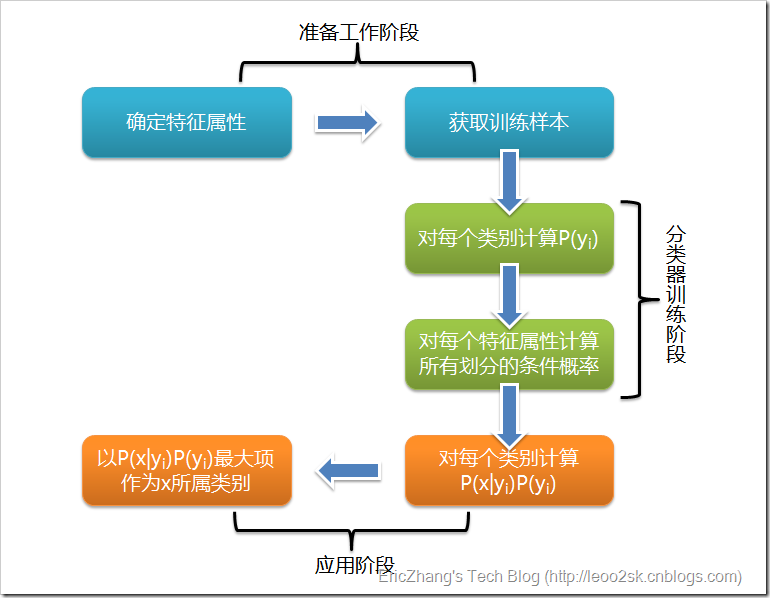
根据上述分析,朴素贝叶斯分类的流程可以由下图表示(暂时不考虑验证):
对于具有多个特征参数的样本,其正态分布的概率密度函数可定义为
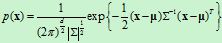
式中,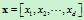 是
是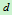 维行向量,
维行向量,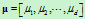 是
是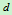 维行向量,
维行向量,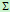 是
是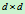 维协方差矩阵,
维协方差矩阵,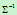 是
是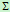 的逆矩阵,
的逆矩阵, 是
是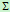 的行列式。
的行列式。
由其判决规则,如果使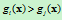 对一切
对一切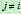 成立,则将
成立,则将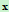 归为
归为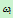 类。
类。
我们根据假设:类别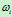 ,i=1,2,……,N的类条件概率密度函数
,i=1,2,……,N的类条件概率密度函数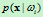 ,i=1,2,……,N服从正态分布,即有
,i=1,2,……,N服从正态分布,即有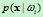 ~
~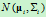 ,那么上式就可以写为
,那么上式就可以写为
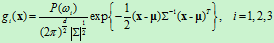
对上式右端取对数,可得
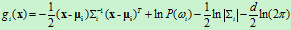
上式中的第二项与样本所属类别无关,将其从判别函数中消去,不会改变分类结果。则判别函数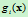 可简化为以下形式
可简化为以下形式
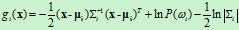
四、实验过程描述
1.产生第一类数据:
x1是第一类数据,x2 是第二类数据,每一列代表一个样本(两个特征)
x1(1,:) = normrnd(14,4,1,20); x1(2,:) = normrnd(20,4,1,20);
x2(1,:) = normrnd(16,4,1,20); x2(2,:) = normrnd(10,4,1,20);
2.均值的估计为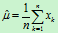
协方差的估计为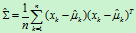 。
。
两类协方差相同的情况下的分类边界为:
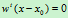 ,
,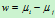
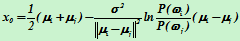
两类协方差不相同的情况下的判别函数为:
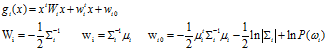
五、实验结果
协方差相同的情况下,判别分类边界其实就是线性分类器产生的边界。在协方差不同的情况下的二次线性分类边界有时会出现奇怪的形状。
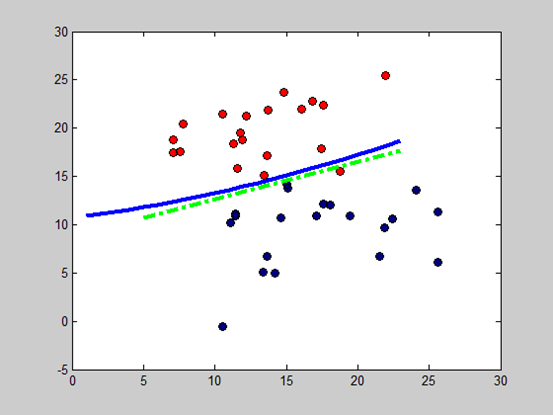
六、附录代码
:
%main.m
clear;clc;
randseed;
x1(1,:) = normrnd(12,4,1,20);%生成高斯分布的随机序列
x1(2,:) = normrnd(20,4,1,20);%均值,标准差,m×n随机向量
plot(x1(1,:),x1(2,:),'ro',...
'LineWidth',1,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[1 0 0],...
'MarkerSize',7)
x2(1,:) = normrnd(18,4,1,20);
x2(2,:) = normrnd(10,4,1,20);
pw1=0.5;
pw2=0.5;
hold on; %新画图像之后不覆盖原图
plot(x2(1,:),x2(2,:),'bo',...
'LineWidth',1,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0 0 0.5],...
'MarkerSize',7)
u1 = sum(x1,2)/20;
u2 = sum(x2,2)/20;
x1count = size(x1,2);
x1t = x1-kron(u1,ones(1,x1count));
S1t = x1t * x1t' / x1count;
x2count = size(x2,2);
x2t = x2-kron(u2,ones(1,x2count));
S2t = x2t * x2t' / x2count;
St = (S1t+S2t)/2;
w = St^(-1) * (u1-u2);
% Y= inv(X) returns the inverse of the square matrix X矩阵求逆
x0 = (u1+u2)/2 - log(pw1/pw2)/((u1-u2)'*inv(St)*(u1-u2)) *(u1-u2);
k=-w(1)/w(2);
b = x0(2)-k*x0(1);
x=[5,23];
plot(x,k*x+b,'g-.','LineWidth',3);
S1tinv = inv(S1t);
S2tinv = inv(S2t);
W1=-1/2 * S1tinv;
W2=-1/2 * S2tinv;
w1=S1tinv*u1;
w2=S2tinv*u2;
%d = det(X) returns the determinant of the square matrix X.矩阵行列式
w10=-1/2 * u1'*S1tinv*u1 - 1/2 *log(det(S1t)) + log(pw1);
w20=-1/2 * u2'*S2tinv*u2 - 1/2 *log(det(S2t)) + log(pw2);
t2=[]
for t1=1:23
%Solve system of nonlinear equations求解非线性方程组
tt2 = fsolve('bayesian_fun',5,[],t1,W1,W2,w1,w2,w10,w20);
t2=[t2,tt2];
end
plot(1:23,t2,'b','LineWidth',3);
% f=bayesian_fun.m
function f=bayesian_fun(t2,t1,W1,W2,w1,w2,w10,w20)
x=[t1,t2]';
f=x'*W1*x+w1'*x+w10 - (x'*W2*x+w2'*x+w20);