oo第一次博客

第一次作业

设计思路

设计了两个类，一个多项式类Polynomial，一个项类Term，其中项包括幂函数及其系数组成。

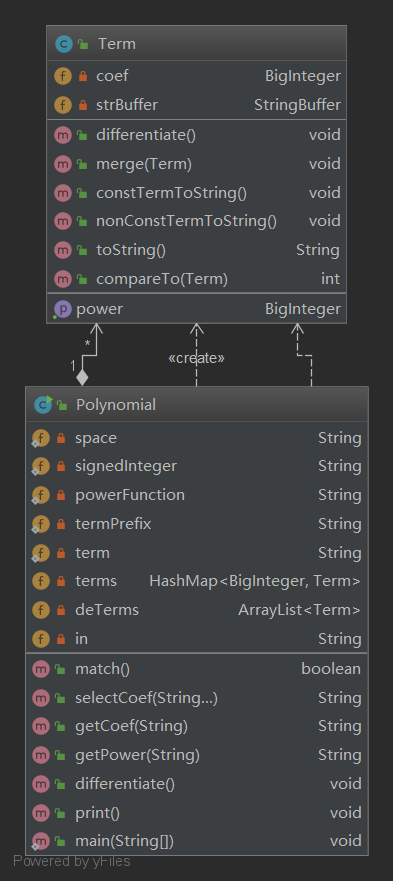
在多项式类中解析出来项，然后之后根据指数的大小存入terms中，在存入的过程中，需要判断是否已经存在该键值，如果存在就需要合并这两项，如此反复，可以保证求导之后不会存在仍可以合并的项，之后将Hashmap中的值都取出来，然后逐项求导，求导的结果仍是一个项。对于结果可以进行以下优化：

1. 第一项尽量为正
2. 系数为0不进行输出
3. 指数为1时不输出次数
4. 如果求导后的所有结果没有输出那么输出0

度量

由于在循环比配产生新的项的过程中，需要判断是否存在才能插入，所以时间复杂度较高。

bug

鉴于第一次作业的合法长度可以非常长，直接使用正则表达式会爆栈，所以采用了两个计数器，记录了当前匹配的字符串的头部和尾部，如果发现某次匹配的头部于上次匹配的尾部不相接，那么就认为没有成功匹配。不过这个使得度量的效果变得不是那么好

第二次作业

设计思路

由于加入了sin，cos。这次根据sin的次数，cos的次数和幂函数的次数以及常系数来确定一个项，所以相比第一次作业，多创建了一个Order类保存和次数相关的信息(sin的次数，cos的次数，幂函数的次数)，并重写了Hashcode和Equals来为之后的Hashmap查找提供方便。

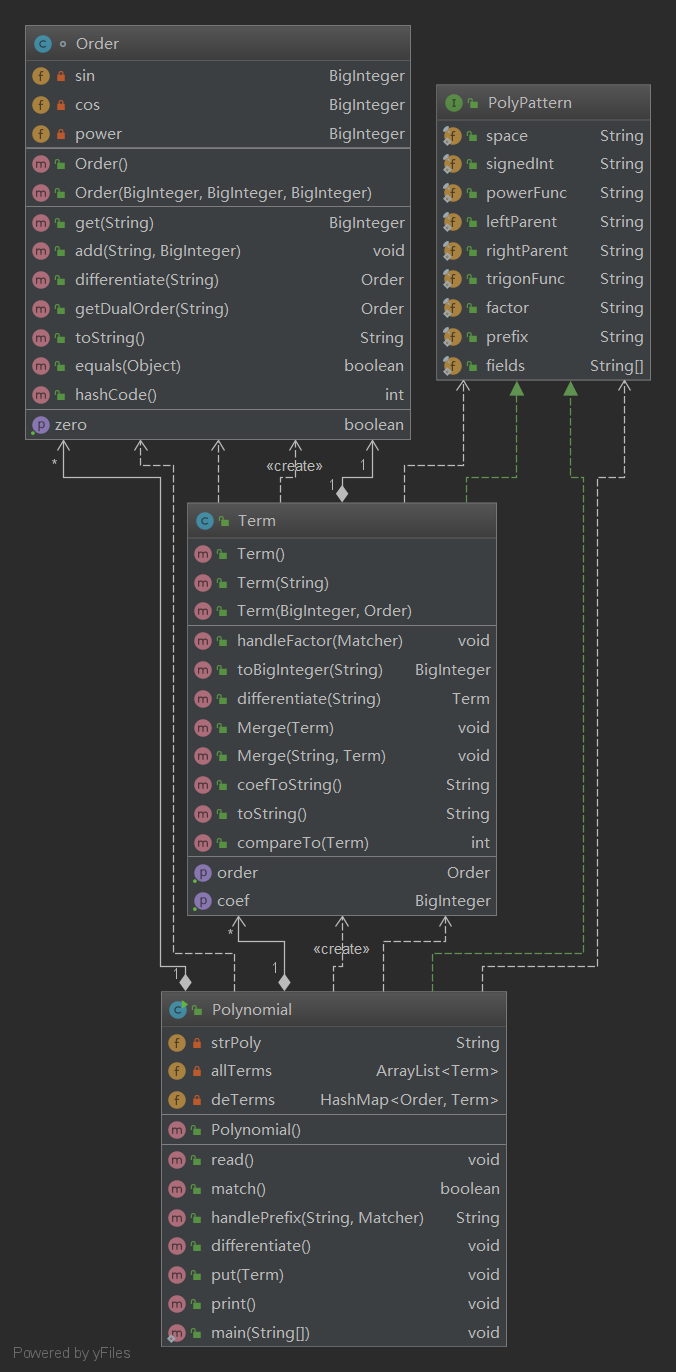
与第一次作业相比这里需要优化的情况比较多，除了第一次作业可以优化的情况之外，我只考虑了以下几种情况

1. sin^2*f(x) + cos^2*f(x) = f(x)
2. f(x) - sin^2*f(x) = cos^2*f(x)
3. f(x) - cos^2*f(x) = sin^2*f(x)

public void put(Term t) {
        Term t1;
        Term t2;
        Term t3;
        Term t4;
        Term mergeTerm;
        Order o;
        Order o1;
        Order o2;
        Order o3;
        Order o4;
        while (true) {
            o = t.getOrder();
            o1 = o.getDualOrder("sin");
            o2 = o.getDualOrder("cos");
            o3 = o.getDualOrder("1-sin");
            o4 = o.getDualOrder("1-cos");
            t1 = deTerms.get(o1);
            t2 = deTerms.get(o2);
            t3 = deTerms.get(o3);
            t4 = deTerms.get(o4);
            /**
             * whether there is a same one or dual one
             * when comes in we can make sure, no duplicate term,
             * because last step has merged all the terms it can
             * merge
             */
            if (deTerms.containsKey(o)) {
                mergeTerm = deTerms.remove(o);
                t.Merge(mergeTerm);
            } else if (t1 != null && t1.getCoef().equals(t.getCoef())) {
                deTerms.remove(o1);
                t.Merge("sin", t1);
            } else if (t2 != null && t2.getCoef().equals(t.getCoef())) {
                deTerms.remove(o2);
                t.Merge("cos", t2);
            } else if (t3 != null &&
                    t3.getCoef().equals(t.getCoef().negate())) {
                deTerms.remove(o3);
                t.Merge("1-sin", t3);
            } else if (t4 != null &&
                    t4.getCoef().equals(t.getCoef().negate())) {
                deTerms.remove(o4);
                t.Merge("1-cos", t4);
            } else {
                break;
            }
        }

度量

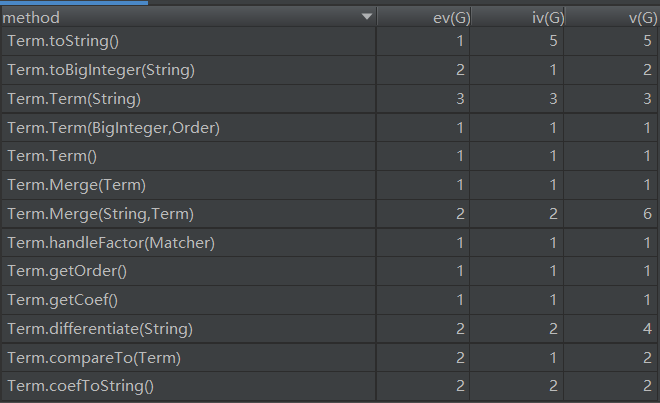
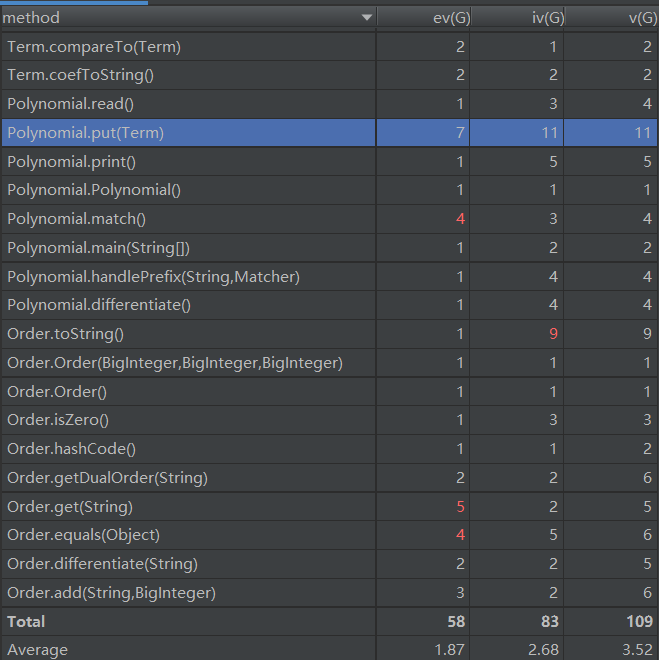
 由于涉及到输出优化所以toString的复杂度较高，这里考虑将其中的有关部分提出重写一个函数来实现。

第三次作业

设计思路

为了能够将复杂的表达式解析出来，写了一个词法和语法分析单元，利用自顶向下的方式来分析，每次匹配记录当前的字符的位置，如果匹配就移动当前指针，词法分析和语法分析可以采用面向对象的方式来实现，并且可以同时利用Matcher类和Pattern类，简化匹配过程。

public boolean match(String s) {
        if (cc < strExp.length()) {
            pattern = Pattern.compile(s);
            matcher = pattern.matcher(strExp.substring(cc));
            if (matcher.lookingAt()) {
                cc += matcher.end();
                return true;
            } else {
                return false;
            }
        } else {
            return false;
        }
    }

由于在不同的类(factor的不同子类)中都需要用到Lexer，所以这里使用了单例模式来实现不同类对于同一个Lexer对象的共享

    private Lexer() {
    }

    private static Lexer instance;

    public static Lexer getInstance() {
        if (null == instance) {
            instance = new Lexer();
        }
        return instance;
    }

在因子类factor中利用静态工厂的方法来创建因子对象，并递归下降分析，同时实现语法分析

 public static Factor newInstance() {
        Lexer lexer = Lexer.getInstance();
        if (lexer.match(signedInt)) {
            return new ConstFactor();
        } else if (lexer.match(powerHead)) {
            return new PowerFactor();
        } else if (lexer.match(trigonHead)) {
            return new TrigonFactor();
        } else if (lexer.match(leftParent)) {
            ExprFactor e = new ExprFactor();
            if (lexer.match(rightParent)) {
                return e;
            } else {
                lexer.error();
            }
        } else {
            lexer.error();
        }
        return null;
    }

其中的Pattern在PolyPattern中定义，为了实现全局变量定义了一个接口，感觉不太好，不过也没有找到更好的办法

public interface PolyPattern {
    String space = "[	 ]*";

    String signedInt = space + "([+-]?\d+)" + space;

    String powerHead = space + "x" + space;

    String funcOrder = space + "(\^" + signedInt + ")";

    String leftParent = space + "\(" + space;

    String rightParent = space + "\)" + space;

    String trigonHead = space + "(sin|cos)" + leftParent;

    String itemPrefix = space + "([+-])" + space;

    String factorPrefix = space + "(\*)" + space;

}

优化

这次实现优化比较麻烦，所以只实现了较为简单的优化比如项内同项合并，多项式合并同类相，但是对于三角函数的合并没有实现，为了实现优化在抽象类factor，项Term类，表达式中实现了equals，由于不同的子类实现equals的方式不同所以需要重写。

函数组合规则放在combine中

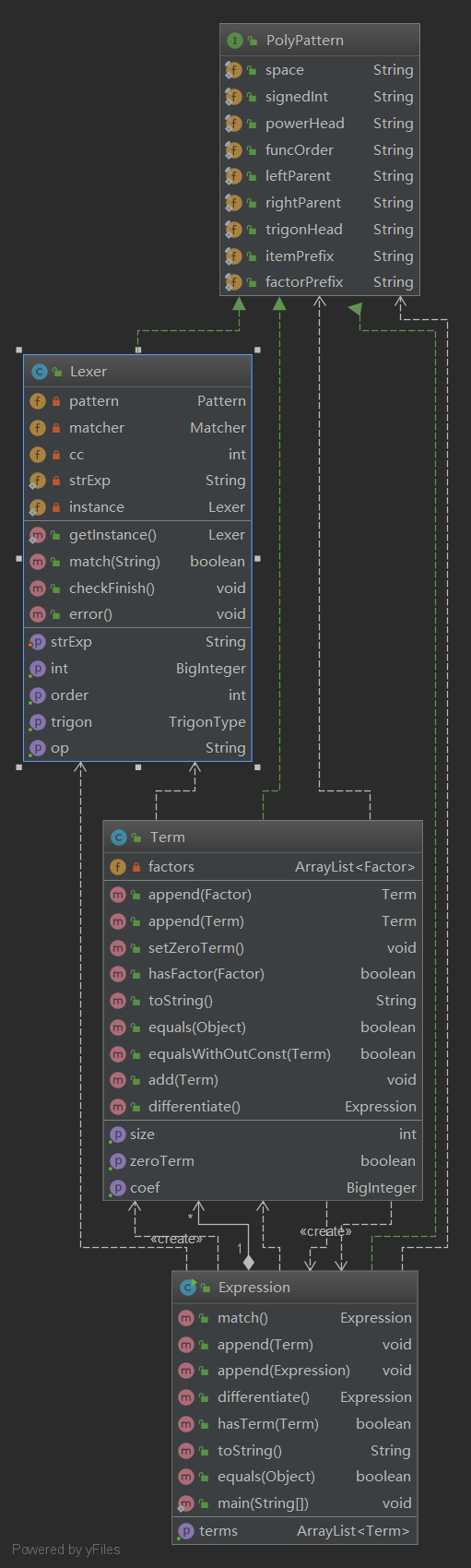
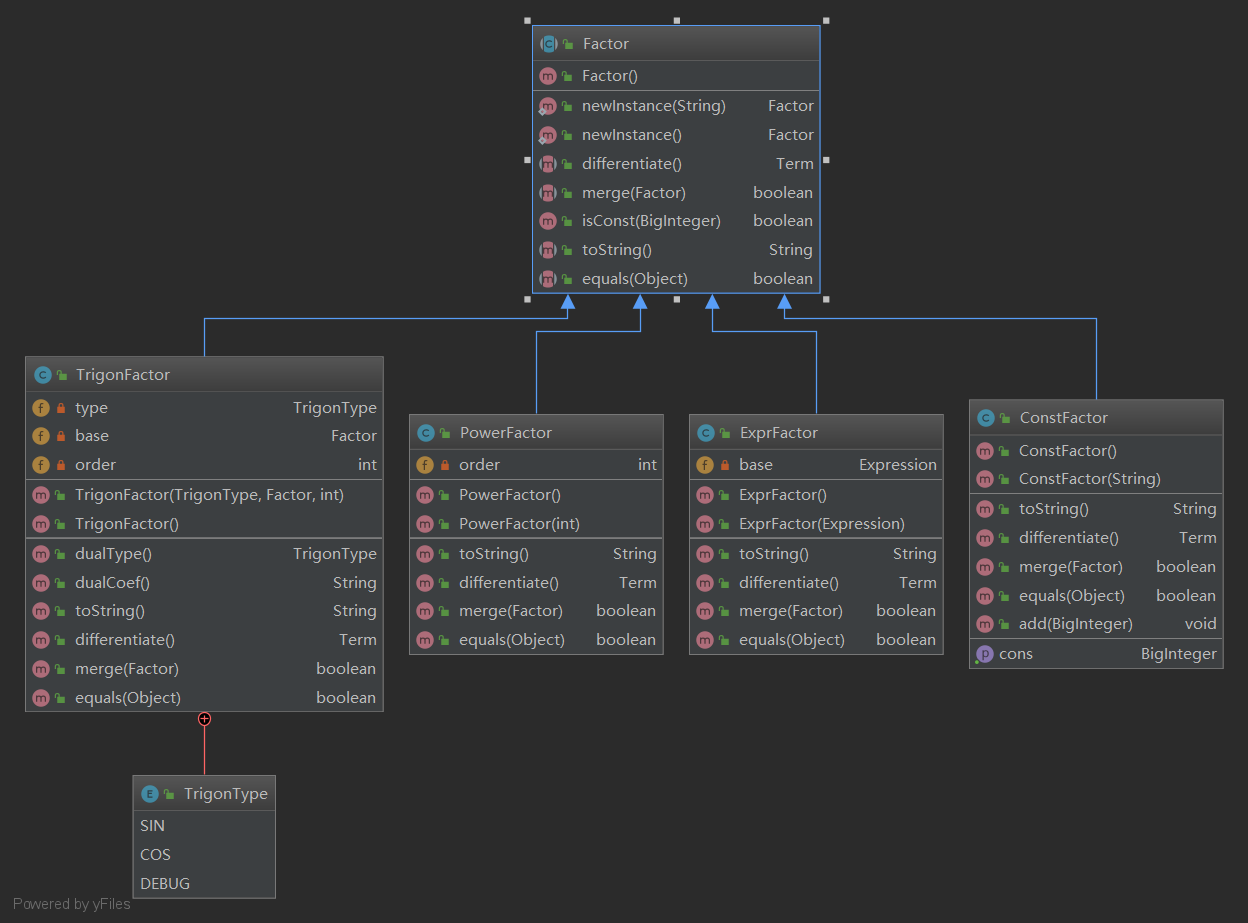
不同类型的factor，即不同类型的函数放在functions中

度量

首先分析函数组合package:combines的度量

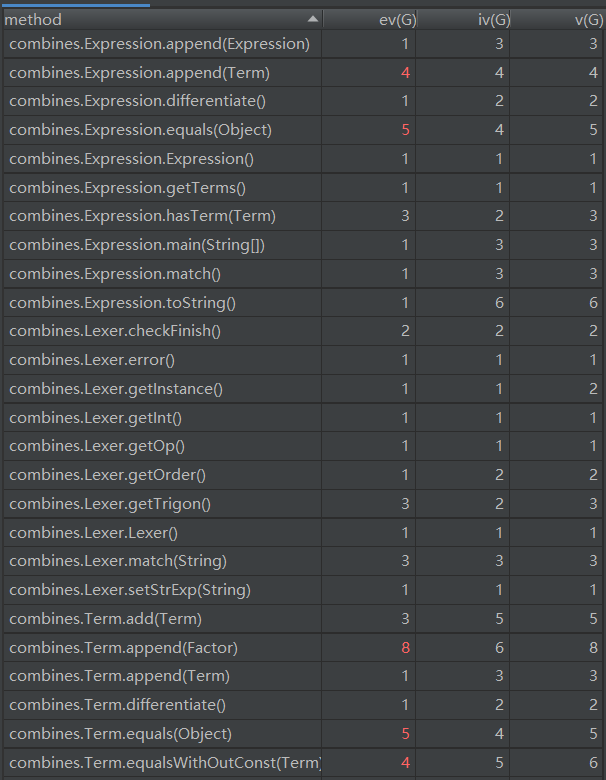
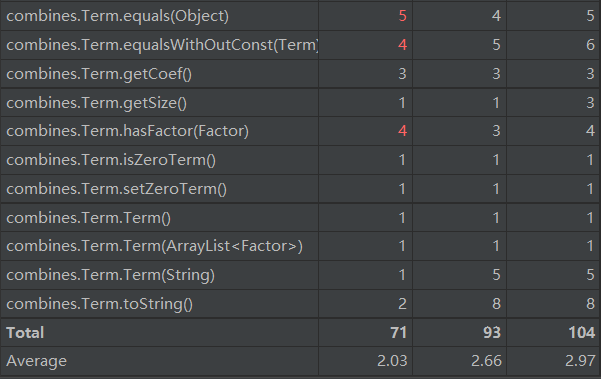
为了实现优化所以这里的链式法则append的方法复杂度过高，需要遍历当前的求导集合来判断是否存在合并的可能，这里可以通过重构数据结构来简化提升。

由于Term中存在上述的优化行为所以复杂度偏高

下面分析不同的函数package: functions的度量

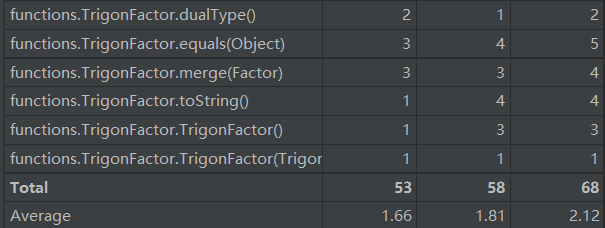
使用静态工厂来创建对象情况较多所以复杂度偏高，暂时没有想到好的解决办法

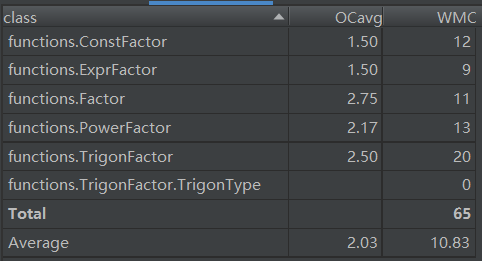
最后看一下整体的内聚和耦合，LCOM的值越大，表示类内聚合度越小，由于Factor中的求导涉及到Factor也涉及Term还有Expression所以类内聚合度较低，其他类的聚合程度还是较高的

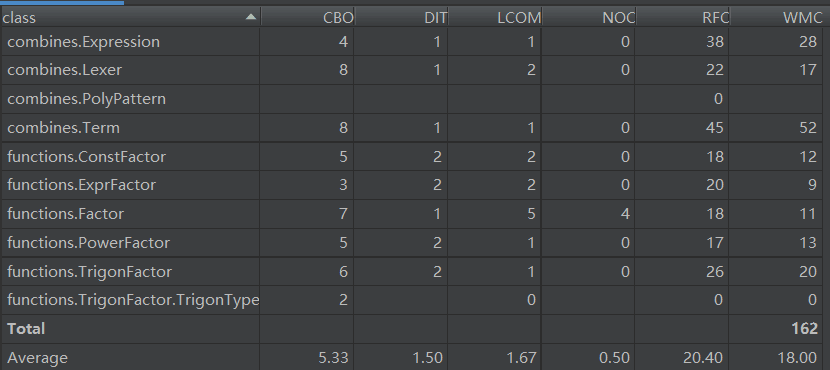
bug

第三次的bug于前两次相比情况都比较复杂，主要集中在优化上面

1. 当一个项是zeroTerm时，即该项有一个0因子的时候，它在后面链接(相乘)其他项或者因子的时候都为0
2. 当和一个项相乘，且这个项是zeroTerm的时候需要将当前项的zeroTerm置为true
3. 在判断能否合并和是否一致的函数中不能使用同一个equals，因为对于常数来说，都是常数即可合并，但是对于多项式中的常数必须完全一致才能认为两个多项式是一致

Applying Creational Pattern

在第三次作业中已经实现了Factory Pattern和Singleton Pattern，之前两次也可以使用这种方式，因为前两次并没有考虑到factor的层次，所以前两次也可以按照第三次的设计方式来设计。