结对编程-四则运算 整体总结
-
学习笔记
-
中缀表达式转换为后缀表达式
- 如果遇到数字,我们就直接将其输出。
- 如果遇到非数字时,若栈为空或者该符号为左括号或者栈顶元素为括号,直接入栈。
- 如果遇到一个右括号,持续出栈并输出符号,直到栈顶元素为左括号,然后将左括号出栈(注意,左括号只出栈,不输出),右括号不入栈。
- 如果遇到运算符号且栈非空,查看栈顶元素,如果栈顶元素的运算优先级大于或者等于该运算符号,则持续出栈,直到栈顶元素优先级小于该运算符。最后将该元素入栈。
- 如果我们读到了输入的末尾,则将栈中所有元素依次弹出。
-
生成随机数的运用
Random ran = new Random();随机数方法创建对象int B = ran.nextInt(2);生成0—1之内的随机数
-
需求分析
-
随机生成题目
- 生成题目数量根据用户需求输入
- 自动生成小学四则运算题目(加、减、乘、除)
- 支持整数和真分数
- 支持多运算符(比如生成包含100个运算符的题目)
-
统计正确率
-
能多次生成题目
-
扩展需求
- 题目去重
- 支持多语言
- 处理生成题目并输出到文件
- 完成题目后从文件读入并判题
-
-
设计思路
- 实验首先是完成一个计算器的功能,可以实现简单的+、-、*、/运算
- 实现多运算符,编入四个类分别实现整数运算、真分数运算、判断结果正确并计算正确率
- 利用JUnit检测非法输入
- 设计一个主类生成随机数,生成题目,并判断正确率
- 设计测试类,利用JUnit测试整数类与分数类的四则运算
uml图:
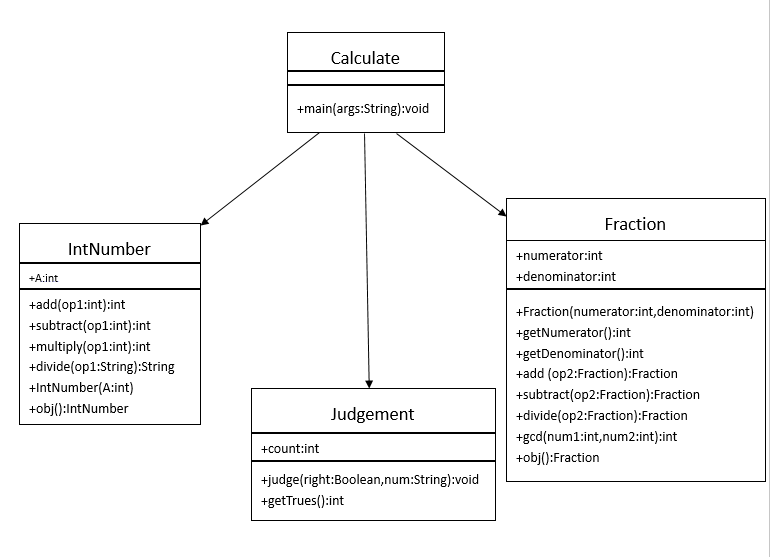
实现真分数计算代码及注释
import java.util.Random;
public class Fraction {
private int numerator, denominator; //定义分母、分子
public Fraction (int numer, int denom)
{
if(denom == 0 ) //分子为0
denom = 1;
if (denom < 0) //若分母小于0,则取分母为正值,分子为负值
{
numer = numer * -1;
denom = denom * -1;
}
numerator = numer;
denominator = denom;
reduce();
}
public int getNumerator()
{
return numerator;
}
public int getDenominator()
{
return denominator;
}
public Fraction add(Fraction op2) //实现真分数加法运算
{
int commonDenominator = denominator * op2.getDenominator(); //两随机数a1、a2的分母相乘,进行通分
int numerator1 = numerator * op2.getDenominator(); //a1的分子=a1的分子与a2的分母相乘
int numerator2 = op2.getNumerator() * denominator; //a2的分子=a2的分子与a1的分母相乘
int sum = numerator1 + numerator2; //将通分过后的两个随机数相加
System.out.print("("+this.toString()+")" + " + " + "("+op2.toString()+")" + "=");
return new Fraction (sum, commonDenominator);
}
public Fraction subtract(Fraction op2) //实现真分数减法运算
{
int commonDenominator = denominator * op2.getDenominator();
int numerator1 = numerator * op2.getDenominator();
int numerator2 = op2.getNumerator() * denominator;
int difference = numerator1 - numerator2;
System.out.print("("+this.toString()+")" + " - " + "("+op2.toString()+")" + "=");
return new Fraction(difference,commonDenominator);
}
public Fraction multiply (Fraction op2) //实现真分数乘法运算
{
int numer = numerator * op2.getNumerator();
int denom = denominator * op2.getDenominator();
System.out.print("("+this.toString()+")" + " * " + "("+op2.toString()+")" + "=");
return new Fraction (numer, denom);
}
public Fraction divide (Fraction op2) //实现真分数除法运算
{
int numer = numerator * op2.getDenominator();
int denom = denominator * op2.getNumerator();
System.out.print("("+this.toString()+")" + " / " + "("+op2.toString()+")" + "=");
return new Fraction (numer, denom);
}
public String toString() //输出格式及限定
{
String result;
if (numerator == 0) //分子为0,结果为0
result = "0";
else
if(denominator == 0) //分母不能为0
return "错误!分母不能为0";
else
if (denominator == 1) //分母为1,结果取分子值
result = numerator + "";
else
result = numerator + "/" + denominator; //按分数形式输出结果
return result;
}
private void reduce()
{
if (numerator != 0)
{
int common = gcd (Math.abs(numerator), denominator); //取分子分母最大公因子
numerator = numerator / common; //约分
denominator = denominator / common;
}
}
private int gcd (int num1, int num2) //计算最大公因子
{
if(num2==0)
return num1;
else
return gcd(num2,num1%num2);
}
public static Fraction obj(){ //生成随机数
Random ran = new Random();
return new Fraction(ran.nextInt(100),ran.nextInt(100));
}
}
测试代码
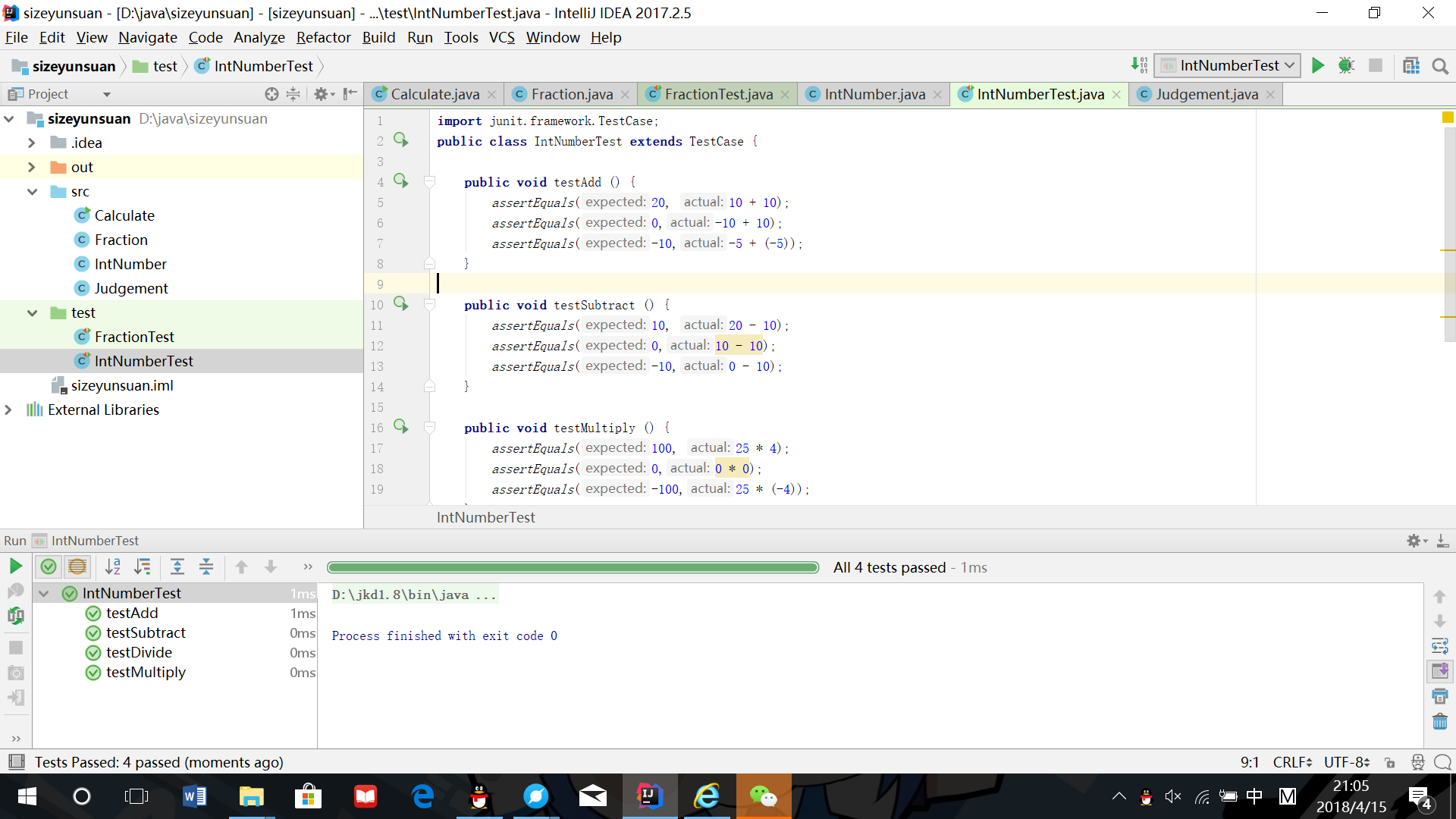
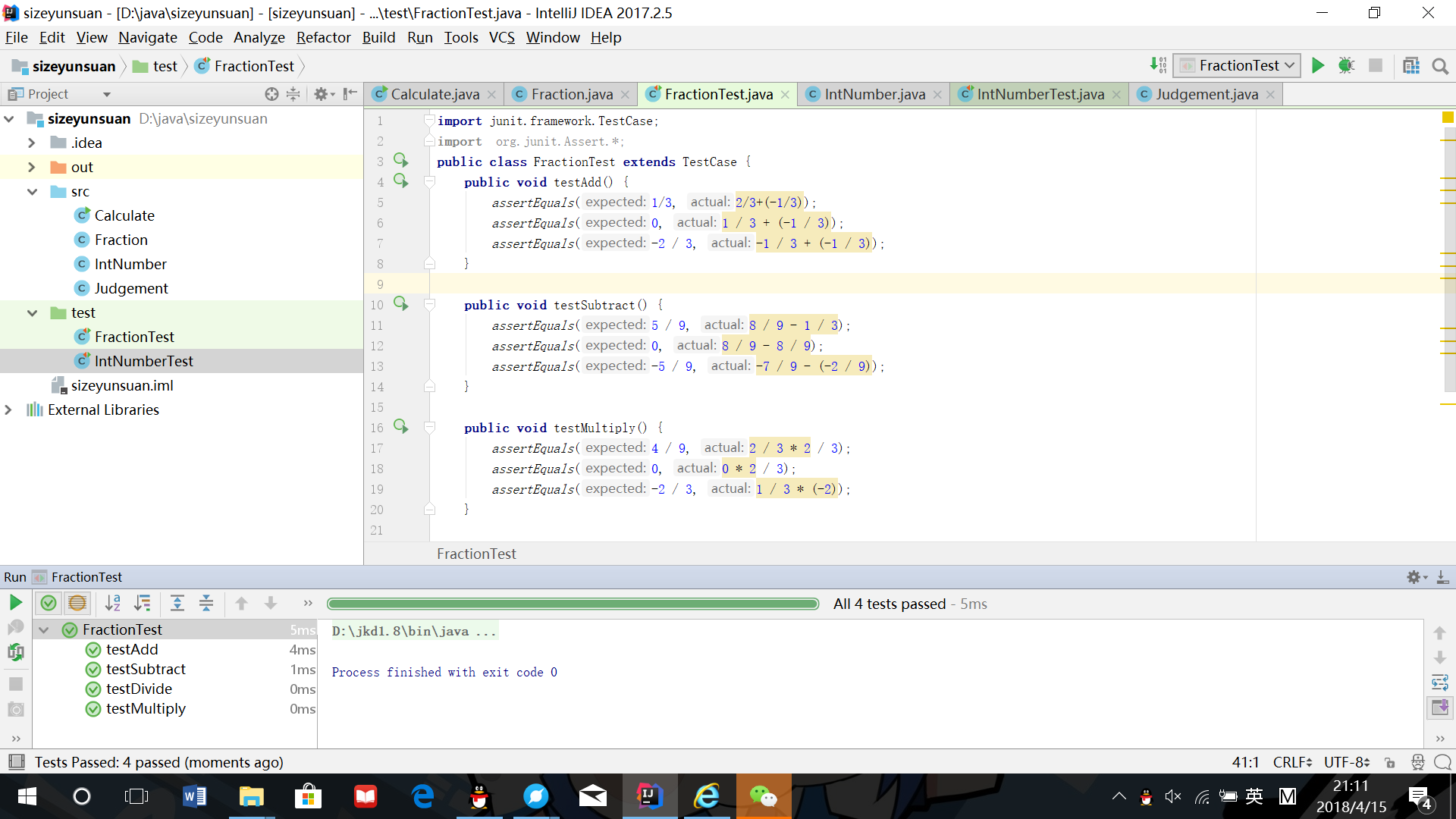
运行结果截图

码云链接
实验过程
- 上次关于真分数的算法我们没有弄明白。这次我们认真讨论并解决了问题。关于代码的批注在上面的代码里。
- 首先是用java语言描述真分数里的加减乘除运算,然后将运算结果化简。
- 化简过程需要用到求最大公因子,这时候我们需要分子分母均为正值,于是就有了
public Fraction (int numer, int denom)方法,以及Math.abs(numerator)来保证算法不出现漏洞。 - 除此之外还要注意分子分母计算的一些限定特性。我们同样加进代码里。
- 代码里的去重功能没写出来,但是经过讨论有了思路:(1)记录之前生成的题目;(2)用遍历比较新生成题目与旧生成题目。如果重复,则删除此新生成题,并再生成一个题目,重新遍历检查。如果不重复,则进入下一环节。
评价我的结队小伙伴
她很美
是天边的火烧云
是日月星辰
但是
我更美
在本周学习中,在小伙伴的帮助下,我对代码有了更深的解读,她的认真及更高效的学习方法让我受益,在这周的磨合中我们的默契度也有了更大的提高,思考问题的时候,会有更多相同的思考,结对学习的过程也是我们相互促进的过程。
总结
- 感受到了有所思路却写不出代码的痛苦,有时候甚至想,为啥不用C编...好吧我的思维还没有转变过来。
- 但是还是很开心,比上周又进步了一点点。开始学着用伪代码,流程图来描述思路给自己的小伙伴看。也让整个算法在脑海里有更清晰的构造。