Description: Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.
A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.
Link: 108. Convert Sorted Array to Binary Search Tree
Examples:
Example 1:
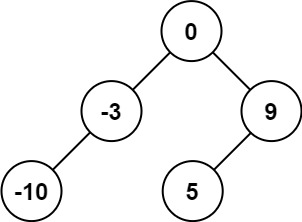
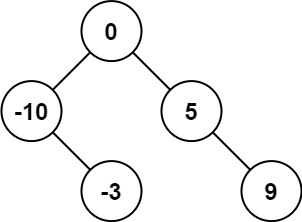
Input: nums = [-10,-3,0,5,9] Output: [0,-3,9,-10,null,5] Explanation: [0,-10,5,null,-3,null,9] is also accepted:
Example 2:
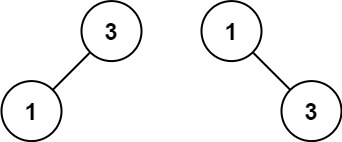
Input: nums = [1,3] Output: [3,1] Explanation: [1,3] and [3,1] are both a height-balanced BSTs.
思路: 首先理解一下二叉搜索树的概念,它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别是二叉搜索树。所以我们发现二叉搜索树也是被递归定义的,左右子树都是二叉搜索树。balanced强调左右子树的节点均衡,所以根节点就是sorted list 的中间节点,左右子树对应的sorted list就是以根节点切分的两部分,以此递归即可,类似之前先中序,后中序构建二叉树。
class Solution(object): def sortedArrayToBST(self, nums): """ :type nums: List[int] :rtype: TreeNode """ if not nums: return None i = int(len(nums)/2) root = TreeNode(nums[i]) root.left = self.sortedArrayToBST(nums[:i]) root.right = self.sortedArrayToBST(nums[i+1:]) return root
类似的题目:109. Convert Sorted List to Binary Search Tree
将sorted array 换成了sorted linkedlist, 所以第一步将链表化为array,然后一样的code.
class Solution(object): def sortedListToBST(self, head): """ :type head: ListNode :rtype: TreeNode """ if head is None: return None nums = [] node = head while node: nums.append(node.val) node = node.next return self.sortedArrayToBST(nums) def sortedArrayToBST(self, nums): if not nums: return None i = int(len(nums)/2) root = TreeNode(nums[i]) root.left = self.sortedArrayToBST(nums[:i]) root.right = self.sortedArrayToBST(nums[i+1:]) return root
日期: 2021-03-15