Leetcode 74. Search a 2D Matrix

Description: Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

• Integers in each row are sorted from left to right.
• The first integer of each row is greater than the last integer of the previous row.

Link: 74. Search a 2D Matrix

Examples:

Example 1:

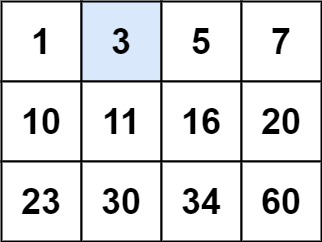
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

思路: 首先确定是在哪一行，然后在这一行二分查找。怎么锁定在哪一行呢？用每行的最大值---最右面一列，结合第一列来确定，如果target <= m行最后一个值，那么target可能在mid行，或者更上面的行，用mid行的最小值确认是否在mid行，如果在，终止循环，如果不在，r = mid - 1。如果target > m行最后一个值, l = mid + 1. 确定了在哪一行，在这个行中普通二分查找就可以。

class Solution(object):
    def searchMatrix(self, matrix, target):
        """
        :type matrix: List[List[int]]
        :type target: int
        :rtype: bool
        """
        if target < matrix[0][0] or target > matrix[-1][-1]:
            return False
        m, n = len(matrix), len(matrix[0])
        l, r = 0, m-1
        i = -1
        while l <= r:
            mid = int((l+r)/2)
            if target <= matrix[mid][-1]:
                if target >= matrix[mid][0]:
                    i = mid
                    break
                else:
                    r = mid - 1
            else:
                l = mid + 1
        if i == -1:
            return False
        l, r = 0, n-1
        while l <= r:
            mid = int((l+r)/2)
            if target == matrix[i][mid]:
                return True
            elif target > matrix[i][mid]:
                l = mid + 1
            else:
                r = mid - 1
        return False

日期: 2021-04-10 渐入佳境啊