时间限制：C/C++语言 1000MS；其他语言 3000MS
内存限制：C/C++语言 65536KB；其他语言 589824KB
题目描述：
给你A数组，询问ΣΣA[gcd(i,j)],1<=i<=n,1<=j<=m
输入
每行有四个整数，N,n,m,p,其中N表示A数组长度,n,m,p为参数;对于A数组如下得出：
A[1]=p,A[x]=(A[x-1]+153)%p
数据范围
小数据 n,m<=N<=1000,p<=1000
大数据 n,m<=N<=100000,p<=100000
输出
输出答案
样例输入
10 1 2 10
样例输出
20
Hint
输入样例2
10 2 2 10
输出样例2
33
样例解释
第一组样例生成的数组A为：10 3 6 9 2 5 8 1 4 7。最后输出的答案为：A[gcd(1,1)] + A[gcd(1,2)] = A[1] + A[1] = 20。
第二组样例生成的数组A为：10 3 6 9 2 5 8 1 4 7。最后输出的答案为：A[gcd(1,1)] + A[gcd(1,2)] + A[gcd(2,1)] + A[gcd(2,2)] = A[1] + A[1] + A[1] + A[2] = 33。
题解
题目给出了一个按规则生成的数组，要求你用两两配对的数（i,j）的最大公约数gcd(i, j) 作为下标计算和。
显然naive的做法是直接生成数组，然后遍历得到和。这样的复杂度是O(NM) --只能过90%的样例。显然在最大情况下10^5 * 10^5就超时了，至少要100s。
由ΣΣA[gcd(i,j)]可以找到一个类似的题目uva 11426，题目要求是：
欧拉函数：
欧拉函数
表示满足 1<=x<=n且与n互质的x的个数。
利用欧拉函数，我们可以如下推理：
因为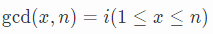 
，
所以x，n除以i 后互质：
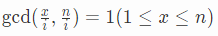
所以，下面是一个关键的思维转换，当n，i确定时，可以求得与n/i互质（且更小）的数的个数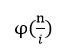
，而这个数乘上i就得到了一个对应的x
设满足gcd(x,n) = i 式的x的可能取值个数可以表示为 g(i,n)，则：
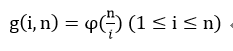
也就是给定了余数和n，我们可以得到满足gcd(x, n) = i的x的个数。剩下的我们只需要统计不同的gcd取值的个数，即可计算得到所需要的和。
具体算法
欧拉函数可以先打表。打表方式见代码。
不妨设n<=m, 我们统计在范围 
内的gcd可能取值，只需要让
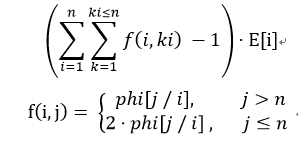
其中phi为欧拉函数表，f(i, j)表示gcd为i，n为j的配对的个数，要考虑i=j的时候多计算了一次，所以要减掉1。
复杂度为N*(1+1/2+1/3...1/N)约为O(NlogN)。
代码如下：
#include<iostream> #include<vector> #include<time.h> #include<stdlib.h> #include<stdio.h> #include<string.h> #include<math.h> using namespace std; int phi[100100];int gcd(int a, int b) { if (b == 0) return a; return gcd(b, a % b); } void phi_table(int n) { memset(phi, 0, sizeof(phi)); phi[1] = 1; for (int i = 2; i <= n; i++) { if (!phi[i]) { for (int j = i; j <= n; j += i) { if (!phi[j]) phi[j] = j; phi[j] = phi[j] / i * (i - 1); } } } } int main() { int N, n, m, p; while (cin >> N >> n >> m >> p) { phi_table(N); vector<int> E(N + 1); E[1] = p; memset(a, 0, sizeof(a)); long long sum = 0; for (int i = 2; i <= N; i++) { E[i] = (E[i - 1] + 153) % p; } if (n > m) { int t = n; n = m; m = t; } for (int i = 1; i <= n; i++) { // 遍历gcd(a, b) 的可能取值 1<=i<=n for (int j = i; j <= m; j += i) { if (j <= n) { int r = phi[j / i] + phi[j / i]; // printf("sum += %d %d %d %d ", i, j, j / i, r); sum += r * E[i]; } else { int r = phi[j / i]; // printf("sum += %d %d %d %d ", i, j, j / i, r); sum += r * E[i]; } } sum -= E[i]; } // DEBUG() // int sum2 = 0; // int* hit = new int[m + 1]; // memset(hit, 0, sizeof(int) * (m + 1)); // for (int i = 1; i <= n; i++) { // for (int j = 1; j <= m; j++) { // int dv = gcd(i, j); // sum2 += E[dv]; // hit[dv]++; // } // } // for (int i = 1; i <= n; i++) { // printf("gcd = %d %d ", i, hit[i]); // } // delete [] hit; // cout << sum2 << endl; // END_DEBUG() cout << sum << endl; } return 0; }
测试样例
输入：
20 3 4 10
10 3 3 10
100000 100000 100000 10
10 1 1 10
输出：
102
79
78421508982
10
参考文献
[1]UVa 11426 - GCD - Extreme (II) https://blog.sengxian.com/solutions/uva-11426