往博客园首页发布,总被无缘无故移出,再也不往首页发布了。一方面需要把内容慢慢丰富起来,一方面个人站点在筹备中。白嫖谷歌云总是遇到问题,奈何学生身份一直申请不下信用卡来,派安盈的美国虚拟银行账户也是遇到各种问题。种种尝试无果,慢慢来吧。
没有申请返校,也就意味着接下来有50天左右的假期。又能好好积累一波,走起~
第二章“模型评估”,具体问题具体分析,针对不同的任务,需要完成的目标不同。如何衡量目标完成的好不好,就是模型评估要做的事情。分类、回归等不同的机器学习任务,需要选择与问题相匹配的评估指标,才能够快速的发现模型选择或者训练过程中出现的问题。其实很多的评估指标,大部分只能片面的反映模型的一部分性能,如果错误的使用了评估指标,不仅不能够发现模型本身的问题,还会给出错误的结论。虽然这些数字指标的定义较晦涩,但理应都是从感性的角度出发得到的评估方式,接下来记录一下本章内容~
1.准确率有什么局限性?
是什么?准确率是指分类正确的样本占总样本个数的比例。
局限性:当不同类别的样本比例非常不均衡时,占比大的类别往往成为影响准确率的最主要因素。
怎样理解?设想一个极端数据集,其中反例占99例,正例占1例。现在设计一个模型,该模型一律将输入内容判断为反例。在该数据集上,模型的准确率达到了99%。该模型是好模型吗?显然不能说是好模型,准确率在这个数据集上并不能反映模型好坏。而如果在正反例均衡的数据集上,存在一个准确率达到99%的模型,那么,就能说这个模型可以将数据集上的数据进行了很好的分类。
解决类别占比不均衡的问题,可以采用每个类别下样本准确率的算数平均值。
2.如何权衡精确率与召回率?
是什么?精确率是指分类正确的正样本个数占分类器判定为正样本的样本个数的比例。召回率是指分类正确的正样本个数占真正的正样本个数的比例。
怎么做?在排序问题中,通常没有一个确定的阈值把得到的结果直接判定为正样本或负样本,而是采用Top N方式返回结果的Precision值和Recall值来衡量排序模型的性能,即认为模型返回的Top N的结果就是模型判定的正样本,然后计算前N个位置上的准确率Precision N和前N个位置上的召回率Recall N。(不懂的百度,这里只是记录这个问答)
如何权衡?比如说为了提高精确率,分类器需要尽量在“更有把握”时才把样本预测为正样本,这样分母小,从而精确率高。但此时会因为过于保守,很多正样本没有被预测出来,导致召回率低。同样的道理,想让召回率高的话,极端情况下把所有数据都预测成正样本,召回率为1了,但失去了精确率。
于是,为了综合评估一个排序模型的好坏,可以绘制P-R曲线。P-R曲线的横轴是召回率,纵轴是精确率。对于一个排序模型来说,其P-R曲线上的一个点代表着,在某一阈值下,模型将大于该阈值的结果判定为正样本,小于该阈值的结果判定为负样本,此时返回结果对应的召回率和精确率。整条P-R曲线是通过将阈值从高到低移动而生成的。
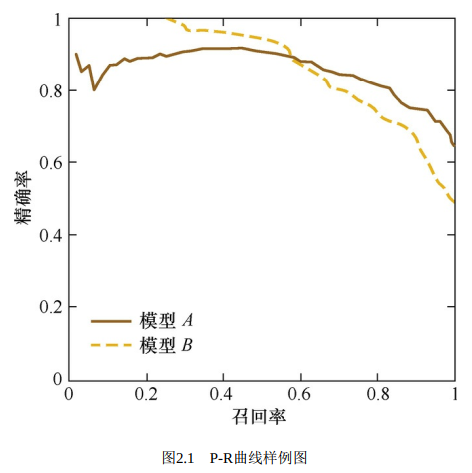
如图2.1所示,随着召回率的增加,精确率整体呈现下降趋势。
3.均方根误差RMSE
RMSE经常被用来衡量回归模型的好坏,一般情况下,RMSE能够很好地反映回归模型预测值与真实值的偏离程度。但在实际问题中,如果存在个别偏离程度非常大的离群点时,即使离群点数量非常少,也会让RMSE指标变得很差。
目前还没有接触过回归问题,对该指标没有一个感性的认识。
4.什么是ROC曲线?
ROC曲线是Receiver Operating Characteristic Curve的简称,中文名为“受试者工作特征曲线”。ROC曲线的横坐标为假阳性率(False Positive Rate,FPR);纵坐标为真阳性率(True Positive Rate,TPR)。
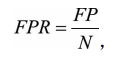
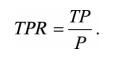
P是真实的正样本的数量,N是真实的负样本的数量,TP是P个正样本中被分类器预测为正样本的个数,FP是N个负样本中被分类器预测为正样本的个数。
5.如何绘制ROC曲线?
类似P-R曲线的绘制过程。通过不断移动分类器的“阈值”来生成曲线上的关键点。一般在二值分类问题中,模型的输出是预测样本为正例的概率。每个样本按照预测概率从高到低排序,指定一个阈值,预测概率大于该阈值的,认为被判定为正例,其余全为负例。不断地调整阈值至最低预测概率值,每一个阈值会对应一对FPR和TPR,在坐标系上绘制每个阈值对应FPR和TPR的位置,再连接所有点得到最终的ROC曲线。
6.如何计算AUC?
AUC指的是ROC曲线下的面积大小,该值能够量化地反映基于ROC曲线衡量出的模型性能。计算AUC值只需要沿着ROC横轴做积分就可以了。
7.ROC曲线相比P-R曲线有什么特点?
同样被经常用来评估分类和排序模型的P-R曲线。相比P-R曲线,ROC曲线有一个特点,当正负样本的分布发生变化时,ROC曲线的形状能够基本保持不变,而P-R曲线的形状一般会发生较剧烈的变化。这个特点让ROC曲线能够尽量降低不同测试集带来的干扰,更加客观地衡量模型本身的性能。这有什么实际意义呢?在很多实际问题中,正负样本数量往往很不均衡。其实从计算方式上可以看到这个区别,假阳性率和真阳性率分别对正负样本做了类似均值化的操作,避免了类别差异大的问题。
若选择不同的测试集,P-R曲线的变化就会非常大,而ROC曲线则能够更加稳定地反映模型本身的好坏。所以,ROC曲线的适用场景更多,被广泛用于排序、 推荐、广告等领域。但需要注意的是,选择P-R曲线还是ROC曲线是因实际问题而异的,如果研究者希望更多地看到模型在特定数据集上的表现,P-R曲线则能够更直观地反映其性能。
8.为什么在一些场景中要使用余弦相似度而不是欧氏距离?
余弦相似度:即两个向量夹角的余弦,关注的是向量之间的角度关系,并不关心它们的绝对大小,其取值范围是[−1,1],相同的两个向量之间的相似度为1。如果希望得到类似于距离的表示,将1减去余弦相似度即为余弦距离。因此,余弦距离的取值范围为[0,2],相同的两个向量余弦距离为0。
欧氏距离:一个通常采用的距离定义,指在m维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离)。
区别:欧氏距离体现数值上的绝对差异,而余弦距离体现方向上的相对差异。
举例:(1)统计两部剧的用户观看行为,用户A的观看向量为(0,1),用户B为(1,0);此时二者的余弦距离很大,而欧氏距离很小;我们分析两个用户对于不同视频的偏好,更关注相对差异,显然应当使用余弦距离。(2)而当我们分析用户活跃度,以登陆次数(单位:次)和平均观看时长(单位:分钟)作为特征时,余弦距离会认为(1,10)、(10,100)两个用户距离很近;但显然这两个用户活跃度是有着极大差异的,此时我们更关注数值绝对差异,应当使用欧氏距离。
9.余弦距离是否是一个严格定义的距离?
该问题属于基础证明类问题,需要清楚“距离”的定义。余弦距离满足正定性和对称性,但是不满足三角不等式,因此它并不是严格定义的距离。详见《百面机器学习》52页。
10.在对模型进行过充分的离线评估之后,为什么还要进行在线A/B测试?
是什么?
Abtest,又称分组隔离实验,是用于衡量网页设计、产品界面不同方案的效果的科学实验方法。具体过程是,为同一个产品目标制定两个方案(如一个界面按钮为蓝色,一个为红色),然后分别为两个方案分配用户流量,同时上线,根据用户的的使用行为效果衡量哪一个方案对于产品目标是有利的,之后就可以将这个方案投入使用。在互联网公司中,A/B 测试是验证新模块、新功能、新产品是否有效,新算法、新模型的效果是否有提升,新设计是否受到用户欢迎,新更改是否影响用户体验的主要测试方法。在机器学习领域中,A/B 测试是验证模型最终效果的主要手段。
为什么?
(1)离线评估无法完全消除模型过拟合的影响,因此,得出的离线评估结果无法完全替代线上评估结果。
(2)离线评估无法完全还原线上的工程环境。一般来讲,离线评估往往不会考虑线上环境的延迟、数据丢失、标签数据缺失等情况。因此,离线评估的结果是理想工程环境下的结果。
(3)线上系统的某些商业指标在离线评估中无法计算。离线评估一般是针对模型本身进行评估,而与模型相关的其他指标,特别是商业指标,往往无法直接获得。比如,上线了新的推荐算法,离线评估往往关注的是ROC曲线、P-R曲线等的改进,而线上评估可以全面了解该推荐算法带来的用户点击率、留存时长、PV访问量等的变化。这些都要由A/B测试来进行全面的评估。
11.如何进行线上A/B测试?
进行A/B测试的主要手段是进行用户分桶,即将用户分成实验组和对照组,对实验组的用户施以新模型,对对照组的用户施以旧模型。在分桶的过程中,要注意样本的独立性和采样方式的无偏性,确保同一个用户每次只能分到同一个桶中,在分桶过程中所选取的user_id需要是一个随机数,这样才能保证桶中的样本是无偏的。
12.如何划分实验组和对照组?
分离目标群体,然后将目标群体对半分开,一半做实验组,一半做对照组。要注意样本的独立性和采样方式的无偏性,确保同一个用户每次只能分到同一个桶中,在分桶过程中所选取的user_id需要是一个随机数,这样才能保证桶中的样本是无偏的。
13.在模型评估过程中,有哪些主要的验证方法,它们的优缺点是什么?
(1)Holdout检验
Holdout 检验是最简单也是最直接的验证方法,它将原始的样本集合随机划分成训练集和验证集两部分。Holdout检验的缺点很明显,即在验证集上计算出来的最后评估指标与原始分组有很大关系。为了消除随机性,研究者们引入了“交叉检验”的思想。
(2)交叉验证
k-fold交叉验证:首先将全部样本划分成k个大小相等的样本子集;依次遍历这k个子集,每次把当前子集作为验证集,其余所有子集作为训练集,进行模型的训练和评估;最后把k次评估指标的平均值作为最终的评估指标。在实际实验中,k经常取10。留一验证:每次留下1个样本作为验证集,其余所有样本作为测试集。在样本总数较多的情况下,留一验证法的时间开销极大。
(3)自助法
自助法是基于自助采样法的检验方法。对于总数为n的样本集合,进行n次有放回的随机抽样,得到大小为n的训练集。n次采样过程中,有的样本会被重复采样,有的样本没有被抽出过,将这些没有被抽出的样本作为验证集,进行模型验证,这就是自助法的验证过程。
14.在自助法的采样过程中,对n个样本进行n次自助抽样,当n趋于无穷大时,最终有多少数据从未被选择过?
当样本数很大时,大约有36.8%的样本从未被选择过,可作为验证集。证明过程详见《百面机器学习》59页。
15.超参数有哪些调优方法?
超参数调优,除了根据经验设定所谓的“合理值”之外,一般很难找到合理的方法去寻找超参数的最优取值。为了进行超参数调优,我们一般会采用网格搜索、随机搜索、贝叶斯优化等算法。网格搜索可能是最简单、应用最广泛的超参数搜索算法,它通过查找搜索范围内的所有的点来确定最优值;随机搜索的思想与网格搜索比较相似,只是不再测试上界和下界之间的所有值,而是在搜索范围中随机选取样本点。网格搜索和随机搜索在测试一个新点时,会忽略前一个点的信息;而贝叶斯优化算法则充分利用了之前的信息,该算法通过对目标函数形状进行学习,找到使目标函数向全局最优值提升的参数。具体内容需要深入学习。
16.在模型评估过程中,过拟合和欠拟合具体是指什么现象?
过拟合是指模型对于训练数据拟合呈过当的情况,反映到评估指标上,就是模型在训练集上的表现很好,但在测试集和新数据上的表现较差。欠拟合指的是模型在训练和预测时表现都不好的情况。
17.降低过拟合和欠拟合风险的方法有哪些?
降低“过拟合”风险的方法
(1)从数据入手,获得更多的训练数据。因为更多的样本能够让模型学习到更多更有效的特征,减小噪声的影响。(数据增强,GAN生成训练样本)
(2)降低模型复杂度。数据较少时,模型过于复杂是产生过拟合的主要因素,适当降低模型复杂度可以避免模型拟合过多的采样噪声。(网络层数、神经元个数、决策树剪枝)
(3)正则化方法。给模型的参数加上一定的正则约束,比如将权值的大小加入到损失函数中。相当于在优化原来的目标函数的同时,也能避免权值过大带来的过拟合风险。
(4)集成学习方法。集成学习是把多个模型集成在一起,来降低单一模型的过拟合风险,如Bagging方法。
降低“欠拟合”风险的方法
(1)添加新特征。当特征不足或者现有特征与样本标签的相关性不强时,模型容易出现欠拟合。
(2)增加模型复杂度。简单模型的学习能力较差,通过增加模型的复杂度可以使模型拥有更强的拟合能力。
(3)减小正则化系数。正则化是用来防止过拟合的,但当模型出现欠拟合现象时,则需要有针对性地减小正则化系数。