Eat the Trees
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 5079 Accepted Submission(s):
2628
Problem Description
Most of us know that in the game called DotA(Defense of
the Ancient), Pudge is a strong hero in the first period of the game. When the
game goes to end however, Pudge is not a strong hero any more.
So Pudge’s teammates give him a new assignment—Eat the Trees!
The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.
Now Pudge has a question, how many ways are there to eat the trees?
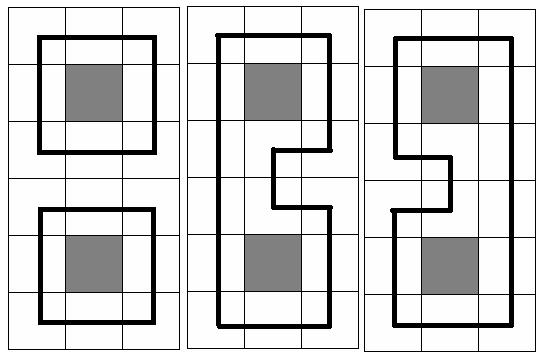
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))
So Pudge’s teammates give him a new assignment—Eat the Trees!
The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.
Now Pudge has a question, how many ways are there to eat the trees?
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))

Input
The input consists of several test cases. The first
line of the input is the number of the cases. There are no more than 10
cases.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.
Output
For each case, you should print the desired number of
ways in one line. It is guaranteed, that it does not exceed 263 – 1.
Use the format in the sample.
Sample Input
2
6 3
1 1 1
1 0 1
1 1 1
1 1 1
1 0 1
1 1 1
2 4
1 1 1 1
1 1 1 1
Sample Output
Case 1: There are 3 ways to eat the trees.
Case 2: There are 2 ways to eat the trees.
Source
Recommend
Solution
之前某次线上赛做过的题,还记得当时调到shi都过不了....
重做一遍咸鱼翻身!
然而这道题几乎就是插头DP模板题叻,相对于普通的轮廓线每位代表的是一个格子,插头DP的轮廓线每一位代表的是每个边框。
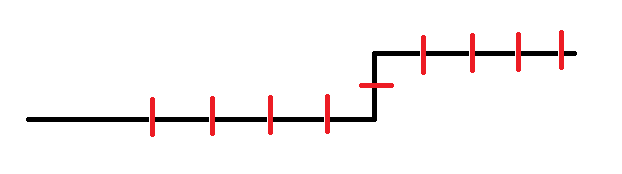
如上图,每根红线代表的是插头DP中状态的每一位,特别的地方就在最后一位,那条横线,表示的是当前格子被更新时左边是否有向右的插头,而当前格子上面的竖线表示上面是否有向下的插头...
这样,插头DP的状态就比普通轮廓线多一位。
这两个位置就是转移的重点。
在当前格子上面有插头或者左边有插头,那么可以转移到当前向右或者向下;如果两个状态同时存在,那么将两个状态合并,不能新增插头;如果两个状态都不存在,并且没有障碍格,那么同时增加两个新插头。
第一列、最后一排、最后一列需要特判。
空间要开足!!!
Code
#include<bits/stdc++.h> #define LL long long using namespace std; int n, m, G[12][12], ti; LL dp[2][(1 << 12)]; int main() { int T; scanf("%d", &T); while(T --) { scanf("%d%d", &n, &m); for(int i = 1; i <= n; i ++) for(int j = 1; j <= m; j ++) scanf("%d", &G[i][j]); memset(dp, 0, sizeof(dp)); int now = 0; dp[now][0] = 1; for(int i = 1; i <= n; i ++) { for(int j = 1; j <= m; j ++) { now ^= 1; memset(dp[now], 0, sizeof(dp[now])); for(int s = 0; s < (1 << m + 1); s ++) { int pre = s & (1 << m); int las = s & 1; if(!G[i][j]) { int ss = (s << 1); if(!pre && !las) dp[now][ss] += dp[now ^ 1][s]; } else { if(j != 1) { if(pre && las) { int ss = (s ^ pre ^ las) << 1; dp[now][ss] += dp[now ^ 1][s]; } if(pre && !las) { int ss = (s ^ pre) << 1 | 1; if(j != m) dp[now][ss] += dp[now ^ 1][s]; ss = (s ^ pre) << 1 | 2; if(i != n) dp[now][ss] += dp[now ^ 1][s]; } if(!pre && las) { int ss = (s ^ las) << 1 | 1; if(j != m) dp[now][ss] += dp[now ^ 1][s]; ss = (s ^ las) << 1 | 2; if(i != n) dp[now][ss] += dp[now ^ 1][s]; } if(!pre && !las) { int ss = s << 1 | 3; dp[now][ss] += dp[now ^ 1][s]; } } else if(j == 1 && !las) { if(pre) { int ss = (s ^ pre) << 1 | 2; if(i != n) dp[now][ss] += dp[now ^ 1][s]; ss = (s ^ pre) << 1 | 1; if(j != m) dp[now][ss] += dp[now ^ 1][s]; } else { if(i != n && j != m) { int ss = s << 1 | 3; dp[now][ss] += dp[now ^ 1][s]; } } } } } } } printf("Case %d: There are %lld ways to eat the trees. ", ++ti, dp[now][0]); } }