

Solution
签到水题,直接状压枚举所有情况算出答案即可。
Code
#include<bits/stdc++.h> #define LL long long using namespace std; inline LL read() { LL x = 0, t = 0; char ch = getchar(); while(!isdigit(ch)) t |= (ch == '-'), ch = getchar(); while(isdigit(ch)) x = x * 10 + ch - '0', ch = getchar(); return x * (t ? -1 : 1); } LL n; LL oi, wh, a[20], b[20], c[20], d[20]; void cal(int s) { oi = wh = 0; for(int i = 1; i <= n; i ++) { int t = (s >> (i - 1)) & 1; if(t) { wh += a[i]; oi = max(1ll * 0, oi - b[i]); } else { oi += c[i]; wh = max(1ll * 0, wh - d[i]); } } } int main() { freopen("week.in", "r", stdin); freopen("week.out", "w", stdout); n = read(); for(int i = 1; i <= n; i ++) { a[i] = read(), b[i] = read(), c[i] = read(), d[i] = read(); } LL ans = 0; for(int s = 0; s < (1 << n); s ++) { cal(s); ans = max(ans, oi * wh); } printf("%lld", ans); return 0; }




Solution
考完看题解泪流满面了QAQ
题中不断强调两点之间只有一条简单路径啊!!!那不就是树嘛QAQ
而且在特定的一个矩阵中也要满足这个性质,那么这个矩阵中所有联通块相当于森林,显然联通块数等于点数减边数。
所以对每个点特定向上和向左建边,用矩阵前缀和处理就好了。
主要是统计答案时发现第一排会多出来向上连的边不能算,第一列会多出来向左连的边不能算,所以预处理时同时处理出每列向上连的边数前缀和,每行向左连的边数的前缀和,最后单独加上这两排的贡献即可。
Code
#include<bits/stdc++.h> #define LL long long using namespace std; inline int read() { int x = 0, t = 0; char ch = getchar(); while(!isdigit(ch)) t |= (ch == '-'), ch = getchar(); while(isdigit(ch)) x = x * 10 + ch - '0', ch = getchar(); return x * (t ? -1 : 1); } int n, m, q; LL G[2005][2005], B[2005][2005], h[2005][2005], l[2005][2005], b[2005][2005]; char a[2005][2005]; int main() { freopen("duty.in", "r", stdin); freopen("duty.out", "w", stdout); n = read(), m = read(), q = read(); for(int i = 1; i <= n; i ++) scanf("%s", a[i] + 1); for(int i = 1; i <= n; i ++) for(int j = 1; j <= m; j ++) { if(a[i][j] == '1') b[i][j] = 1; l[i][j] = l[i - 1][j], h[i][j] = h[i][j - 1]; if(b[i][j]) { G[i][j] ++; if(b[i - 1][j]) B[i][j] ++, l[i][j] ++; if(b[i][j - 1]) B[i][j] ++, h[i][j] ++; } G[i][j] += G[i - 1][j] + G[i][j - 1] - G[i - 1][j - 1]; B[i][j] += B[i - 1][j] + B[i][j - 1] - B[i - 1][j - 1]; } for(int i = 1; i <= q; i ++) { int a1 = read(), b1 = read(), a2 = read(), b2 = read(); LL ans1 = G[a2][b2] - G[a2][b1 - 1] - G[a1 - 1][b2] + G[a1 - 1][b1 - 1]; LL ans2 = B[a2][b2] - B[a2][b1] - B[a1][b2] + B[a1][b1]; ans2 += h[a1][b2] - h[a1][b1] + l[a2][b1] - l[a1][b1]; printf("%lld ", ans1 - ans2); } return 0; }



Solution
考试的时候真没看出来是逆序对QAQ
题中给的式子简直是骗人!!想了半天怎么可能统计出每个点QAQ!!
所以把式子分析,实际上对于加入每条线的增加贡献,就等于与在它之前加入并它相交的线的条数。
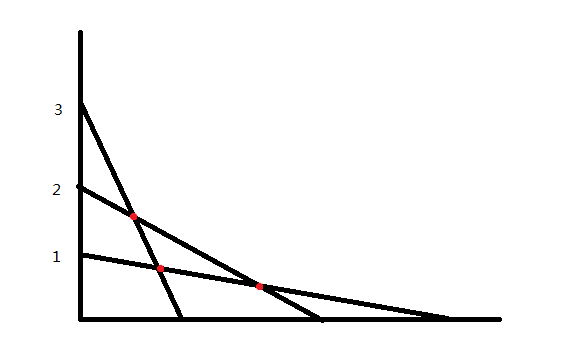

如上图,两种情况得到的贡献实际上是一样的,第一张图在加入2时加了1的贡献,在加入3的时候加了2的贡献,第二张图同理。
考虑线段相交的性质.显然有这样的结论:0 < a < b,0 < c < d,那么在(0,a),(c,0)之间连线段,在(0,b),(d,0)之间连线段,这样的两条线段在第一象限一定没有交点.
答案就是x[1],x[2]…x[n]这个序列的逆序对个数.
考虑树状数组算法,我们需要求出第i个元素和前面i-1个元素形成的逆序对个数.
整个序列由若干段等差数列组成(不超过a段)(题目描述有“x[i]互不相同”).而第i个元素前面的i-1个元素也可以分成不超过a段等差数列.在每段等差数列内大于第i个元素的元素个数可以O(1)求出,因此O(a)的时间内即可求出第i个元素和前面i-1个元素组成的逆序对数.时间复杂度O(na).
可以得到a<=10时的20分.结合算法3可以得到60分.
x[1]=a的数据告诉我们,x[i]=i*a%mod
假设x[i]=x[i-1]+a(也就是x[i-1]+a < mod),且x[i-1]和前面所有数字形成了m个逆序对,同时,除去x[i-1]和x[i]所在的等差数列,x[i]前面的所有数字可以分成k段等差序列,那么x[i]将和前面所有数字组成m-k个逆序对.
原因在于:每段等差序列中必然有一个数字和x[i-1]能组成逆序对,但不能和x[i]组成逆序对.那么每段等差数列的贡献都会减1.
因此我们可以O(1)从x[i-1]的贡献得到x[i]的贡献.
如果x[i] < a,不存在对应的x[i-1],我们需要直接计算它的贡献.前面有i-1个数字,我们数出有多少个数字不产生贡献(即小于x[i]的数字个数),即可求出有多少个数字形成了逆序对.用树状数组维护小于a的所有数值,可以在O(loga)的时间内完成一次这样的计算.小于a的数字至多有a个,所以这一部分的时间复杂度为O(aloga),空间复杂度为O(a)
总的时间复杂度为O(aloga+n)
可以得到x[1]=a的20分.
现在x[1]!=a,我们只需针对最开始的一段不完整等差数列加一些特判就可以通过本题.
---------------------
作者:KGV093
来源:CSDN
原文:https://blog.csdn.net/KGV093/article/details/78170128
Code
#include<bits/stdc++.h> using namespace std; inline int read() { int x = 0, t = 0; char ch = getchar(); while(!isdigit(ch)) t |= (ch == '-'), ch = getchar(); while(isdigit(ch)) x = x * 10 + ch - '0', ch = getchar(); return x * (t ? -1 : 1); } int n, x, a, mod; int pre[100005]; int lowbit(int x) { return x & -x; } int query(int x) { int res = 0; for(int i = x; i; i -= lowbit(i)) res += pre[i]; return res; } void add(int x, int d) { for(int i = x; i <= a; i += lowbit(i)) pre[i] += d; } int main() { freopen("fly.in", "r", stdin); freopen("fly.out", "w", stdout); n = read(), x = read(), a = read(), mod = read(); int cur = x, idc = 0; long long ans = 0, rev = 0;; for(int i = 1; i <= n; i ++) { if(cur >= a) { rev -= idc; if(x > cur) ++ rev; ans += rev; } else rev = i - 1 - query(cur + 1), ans += rev, add(cur + 1, 1); cur += a; if(cur >= mod) cur -= mod, ++ idc; } printf("%lld", ans); return 0; }