设高度场由函数z=h(x,y)给出,则问题就是求此曲面的法线。
注:文中d代表偏导数。
方法一:
把z=h(x,y)看成山坡,则在点P(x,y)处,其爬坡方向由二维梯度给出
gradh=(dh/dx,dh/dy,0)。
(gradh在XY平面内,由低海拔指向高海拔)。
根据“梯度的模等于方向导数”有:
|gradh|=tan(theta),theta为坡度角。
因为|gradh|=tan(theta),所以若设up=(0,0,1)(即让up的模为1),则恰有-gradh+up=normal。如图:
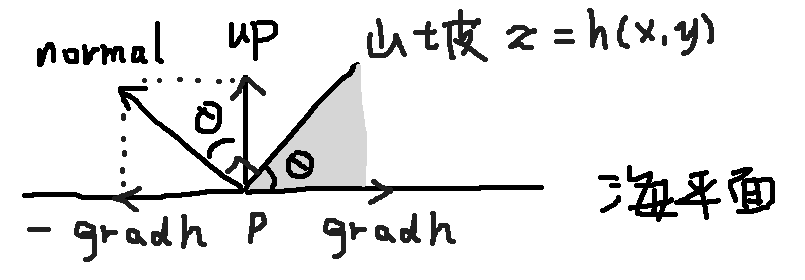
于是就有normal=-gradh+up=-(dh/dx,dh/dy,0)+(0,0,1)=(-dh/dx,-dh/dy,1)。
注:可见,梯度是法线的投影的反方向。
方法二:
构造三维标量场F(x,y,z)=h(x,y)-z。
则z=h(x,y)为F的0等值面(因为z=h(x,y)即F(x,y,z)=0)。
场F在点(x,y,z)处梯度为gradF=(dF/dx,dF/dy,dF/dz)=(dh/dx,dh/dy,-1)。
由于梯度必定垂直于等值面。
所以z=h(x,y)在点(x,y,z)处的法向量normal=gradF=(dh/dx,dh/dy,-1)。
注:
1,方法一 将高度场看作二维标量场(即每个二维点(x,y)对应一个标量值:高度h),利用二维标量场的梯度概念进行求解。方法二 将高度场看作一个三维标量场的等值面,利用三维标量场的梯度概念进行求解。可见两种方法得出的结果是一致的。
2,是取(-dh/dx,-dh/dy,1)还是取(dh/dx,dh/dy,-1)根据需求而定,如本文由高度场求法线这种用于图形学用途,显然是会取(-dh/dx,-dh/dy,1),
3,以上两种方法都没有对结果进行归一化,在实际用于图形学时应进行归一化。
----补充:
方法三:
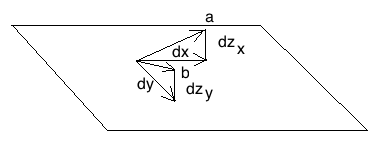
a=(dx,0,dh_x)
b=(0,dy,dh_y)
normal=normalize(axb)=normalize(-dh_x*dy,-dx*dh_y,dx*dy)=normalize(-dh/dx,-dh/dy,1)